2.2简谐运动的描述 课件 （29张PPT）

(共29张PPT)
第二章 机械振动
第2节 简谐运动的描述
思考并回答问题。
思考1：.小提琴可以奏出优美的音乐，小提琴琴弦的运动范围与振幅是什么关系？
[答案] 小提琴琴弦的运动范围是振幅的两倍。
思考2：.如果两个振动存在相位差，它们的振动步调是否相同？
[答案] 不同。
正确的打“√”，错误的打“×”。
（1） 振子从任意一个位置出发又回到这个位置所用的最短时间就是一个周期。( )
×
（2） 振幅越大，弹簧振子的振动周期越大。( )
×
（3） 振动物体的周期越大，表示振动得越快。( )
×
（4） 简谐运动的位移表达式与开始计时时刻物体所在位置无关。( )
×
（5） 做简谐运动的振子一个周期里走过的路程是振幅的4倍。( )
√
任务1 振幅、周期和频率
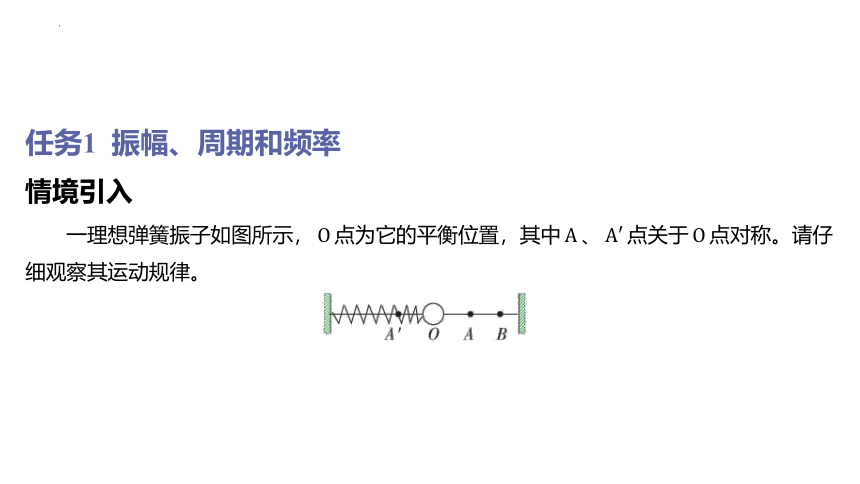
情境引入
一理想弹簧振子如图所示， 点为它的平衡位置，其中 、 点关于 点对称。请仔细观察其运动规律。
问题引领
1.从振子某一时刻经过 点开始计时，至振子下一次再经过 点的时间为一个周期吗？
[答案] 不是。经过一个周期，振子一定从同一方向经过 点，即经过一个周期，位移、速度均第一次与初始时刻的位移、速度相同。
2.先后将振子拉到 点和 点由静止释放，两种情况下振子振动的周期相同吗？振子完成一次全振动通过的位移相同吗？路程相同吗？
[答案] 周期相同，振动的周期取决于振动系统本身，与振幅无关。位移相同，均为零。路程不相同，一个周期内振子通过的路程与振幅有关。
知识生成
1.振幅：振动物体离开平衡位置的①___________，叫作振动的振幅。用 表示，单位为米 。
最大距离
2.全振动：振动物体以相同的速度相继通过②___________所经历的过程。
同一位置
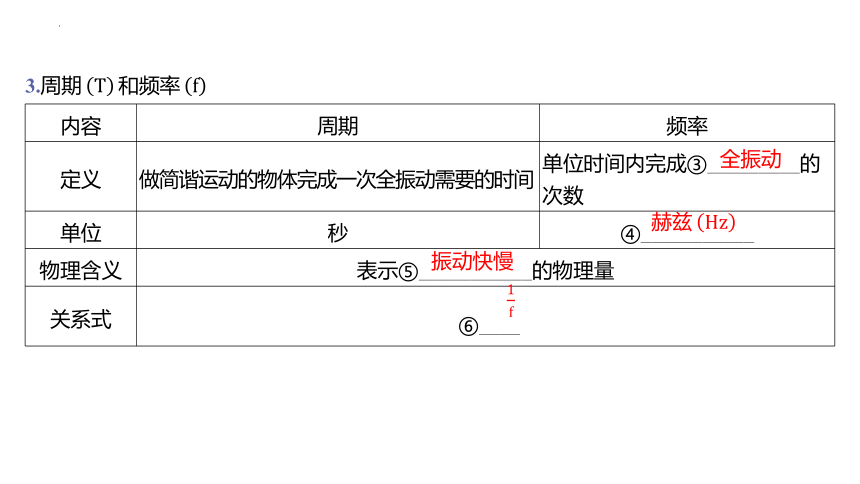
3.周期 和频率
内容 周期 频率
定义 做简谐运动的物体完成一次全振动需要的时间 单位时间内完成③_________的次数
单位 秒 ④___________
物理含义 表示⑤___________的物理量
关系式 ⑥_ ___
全振动
赫兹
振动快慢

应用探究
[活动1].问题讨论：
（1） 同一面鼓，用较大的力敲鼓面和用较小的力敲鼓面，鼓面的振动有什么不同？听上去感觉有什么不同？
[答案] 用较大的力敲，鼓面的振动幅度较大，听到的声音大；反之，用较小的力敲，鼓面的振动幅度较小，听到的声音小。
（2） 将弹簧上端固定，下端悬吊钢球，旁边立一刻度尺，把钢球从平衡位置竖直向下拉一段距离 ，放手让其运动。仔细观察钢球的运动，讨论下列问题：
① 钢球在弹簧原长位置到最低点的距离就是振幅的大小的说法是否成立？
[答案] 不成立。振幅等于钢球从平衡位置到最远距离的长度，平衡位置不是弹簧原长位置。
② 钢球的振幅大，它的位移一定大吗？
[答案] 振幅大，振动物体的位移不一定大，但其最大位移一定大。
[活动2]简谐运动振幅与路程的关系
例1 一个做简谐运动的质点，它的振幅是 ，频率是 ，该质点从平衡位置开始经过 后，位移的大小和经过的路程分别为( @19@ )。
A. B. C. D.
B
[解析] 质点的振动周期 ，故时间 ，所以 末质点在最大位移处，位移大小为 ，质点通过的路程为 ，B项正确。
分析问题.做简谐运动的质点一个周期所走的路程是多少？质点所走的路程与运动时间是否成正比？
【提示】做简谐运动的质点一个周期所走的路程为四个振幅。简谐运动中，质点所走的路程与运动时间不成正比，因为不是匀速直线运动。
振子的路程是标量，是随时间不断增大的。振子在一个周期内的路程为4倍的振幅，在半个周期内的路程为2倍的振幅。
（1）若从特殊位置开始计时，如平衡位置、最大位移处，振子在 周期内的路程等于振幅。
（2）若从一般位置开始计时，振子在 周期内的路程与振幅之间没有确定关系，路程可能大于、等于或小于振幅。
任务2 相位、简谐运动的表达式
情境引入
情境一：并列悬挂两个相同的弹簧振子，如图所示。把小球竖直向下拉同样的距离后同时放开，观察两球的振幅、周期、振动的步调；再次把两个小球拉到相同的位置，先把第一个小球放开，再放开第二个，观察两球的振幅、周期、振动的步调。
情境二：如图，两人合作，模拟绘制振动曲线。先在白纸中央画一条直线 ，使它平行于纸的长边，作为图像的横坐标轴。一个人用手使铅笔尖在白纸上沿垂直于 的方向水平振动，另一个人沿 的方向匀速拖动白纸，纸上就画出了一条描述笔尖振动情况的 图像。请完成这个实验。
问题引领
1.请分别叙述情境一中两种情况下两球的振幅、周期、频率和步调的情况。
[答案] 两个小球同时释放时，除了振幅和周期都相同外，它们的振动步调也一致。如果先后释放小球，它们的振幅和周期相同，但振动步调就不一致。
2.请尝试列出情境二中图线的数学函数表达式，并把表达式中的字母与振动的周期、频率等物理量结合起来。
[答案] 。
知识生成
1.相位
相位：表示振动物体⑦___________的物理量，用来描述振动物体在各个时刻所处的不同状态。
初相位： 时刻的相位称为初相位。
相位差：是指两个相位之差，在实际应用中经常用到的是两个具有相同频率的简谐运动的相位差，设其初相位分别为 和 ，当 时，其相位差 ⑧__________。
不同状态

2.简谐振动的表达式
简谐运动的一般表达式为⑨__________________。
（1） 表示振动物体相对于⑩___________的位移； 表示时间。
（2） 表示简谐运动的 _______。
（3） 叫作简谐运动的“圆频率”，表示简谐运动振动的快慢， （与周期 和频率 的关系）。
（4） 代表简谐运动的 _______， 表示 时的相位，叫作 _________（或初相）。

平衡位置
振幅
相位
初相位
应用探究
[活动1].我们通过前面的学习已经知道做简谐运动的物体的位移 与运动时间 之间满足正（余）弦函数关系，因此，位移 的一般函数表达式可写为 。
请结合数学中正弦函数的表达式和弹簧振子运动的情境分析简谐运动的特点。
[答案] 弹簧振子在某个范围内在平衡位置附近做往复运动，其速度、加速度和位移呈现周期性的变化。
[活动2]简谐运动的周期性和对称性
例2 （多选）如图所示，一水平弹簧振子做简谐运动，周期为 ，则( @32@ )。
A.振子的位移为 和 的两个时刻，振子的速度一定大小相等、方向相反
B.振子的速度为 和 的两个时刻，振子的位移一定大小相等、方向可能相同
C.若 ，则在 时刻和 时刻振子振动的速度一定相等
D.若 ，则在 时刻和 时刻弹簧的长度一定相等
BC
[解析] 振子的位移为 和 的两个时刻，振子的速度一定大小相等，方向可能相同，如图中 、 两点，A项错误；振子的速度为 和 的两个时刻，它的位移可能是相同的，如图中的 、 两点，B项正确；相隔一个周期 的两个时刻，振子位于同一位置，其位移相同，速度也相同，C项正确；相隔 的两个时刻，可能振子的位移大小相等、方向相反，其位置关于平衡位置对称，弹簧分别处于压缩和拉伸状态，也可能两时刻振子均在平衡位置，此时弹簧的长度并不一定相等，D项错误。
分析问题.（1）弹簧振子经过同一位置时速度是否相同？
（2）弹簧振子经过关于平衡位置对称的两点时，速度大小相等吗？
【提示】（1）速度是矢量，既有大小，又有方向，弹簧振子经过同一位置时速度大小相等，方向可能不同，因此速度不同。（2）弹簧振子经过关于平衡位置对称的两点时，速度大小相等。
简谐运动具有重复性，其运动具有对称性和周期性的特点。如图所示：
1.对称性
（1）时间的对称
①物体来回通过相同两点间的时间相等，即 。
②物体经过关于平衡位置对称的等长的两线段的时间相等，图中 ， 。
（2）速度的对称
①物体连续两次经过同一点（如 点）的速度大小相等，方向相反。
②物体经过关于 点对称的两点（如 点与 点）时，速度大小相等，方向可能相同，也可能相反。
（3）位移的对称
①物体经过同一点（如 点）时，位移相同。
②物体经过关于 点对称的两点（如 点与 点）时，位移大小相等、方向相反。
2.周期性
做简谐运动的物体经过一个周期或几个周期后，能回复到原来的状态，因此在处理实际问题时，要注意到多解的可能性。
1.（任务1）某质点做简谐运动的振动图像如图所示，下列说法中正确的是( @35@ )。
A.振幅为 B.频率为
C.周期为 D. 时刻质子的速度方向沿 轴正方向
C
[解析] 由图像可知振幅 ，A项错误； ，频率 ，B项错误，C项正确； 时质点的速度方向沿 轴负方向，D项错误。
2.（任务1）如图所示，弹簧振子以 为平衡位置，在 、 间做简谐运动，则( @37@ )。
A.从 为一次全振动 B.从 为一次全振动
C.从 为一次全振动 D.从 为一次全振动
C
[解析] A项对应过程的路程为2倍的振幅，B项对应过程的路程为3倍的振幅，C项对应过程的路程为4倍的振幅，D项对应过程的路程大于3倍的振幅，又小于4倍的振幅， 、 、 三项错误，C项正确。
3.（任务2）一位游客在长寿湖边想乘游船，当日风浪很大，游船上下浮动。可把游船的浮动简化成竖直方向的简谐运动，振幅为 ，周期为 。当船到达平衡位置时，甲板刚好与码头地面平齐。已知地面与甲板的高度差不超过 时，游客能舒服地登船。在一个周期内，游客能舒服地登船的时间总共是( @39@ )。
A. B. C. D.
B
[解析] 假设 时刻船刚好到达平衡位置且向上运动，则船的振动方程可写为 ；在第一个周期内 的时刻分别为 ， ， ， ，其中满足题意要求的时间范围是 、 、 ，所以在一个周期内，游客能舒服地登船的时间 ，B项正确。
4.（任务2）用频闪照相的方法拍到的一个水平放置的弹簧振子的振动情况如图所示。图1是振子静止在平衡位置的照片，图2是振子被拉伸到左侧距平衡位置 处，放手后向右运动 周期内的频闪照片。已知频闪的频率为 。
（1） 求相邻两次闪光的时间间隔 和弹簧振子振动的周期 。
（2） 若振子的质量为 ，弹簧的劲度系数为 ，则振子的最大加速度是多少？
[答案] （1） （2）
[解析] （1）频闪照相周期 ，即相邻两次闪光的时间间隔 ，振子从最大位移处运动到平衡位置经历的时间为 ，故振子的振动周期 。
（2）振子的最大加速度 。