2022-2023学年高二上学期数学人教A版(2019)数学选择性必修第一册2.3.1两条直线的交点坐标 课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)数学选择性必修第一册2.3.1两条直线的交点坐标 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 997.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 21:35:54 | ||
图片预览





文档简介
(共19张PPT)
第二章:直线和圆的方程
2.3.1 :两条直线的交点坐标
数学组:刘华海 吕佩玲
名称
方程的形式
已知条件
方程直线的局限性
一般式
点斜式
斜截式
两点式
截距式
(x1,y1)是直线上一点,k是斜率
k是斜率,b是直线在y轴上的截距
不包括与x轴垂直的直线
a是直线在x轴上的截距,b是直线在y轴上的截距
(x1,y1),(x2,y2)是直线上两点
不包括与x轴垂直的直线
不包括与坐标轴垂直的直线
Ax+By+C=0
(A、B不同时为零)
A、B、C为常数
任何位置的直线
不包括与坐标轴垂直的直线,不包括过原点的直线。
回顾引入
直线方程的五种形式
一、学习目标
1.会用解方程组的方法求两条相交直线的交点坐标.
2.能根据方程组解的个数判断两条直线的位置关系.
3.核心素养:数学运算、直观想象、逻辑推理.
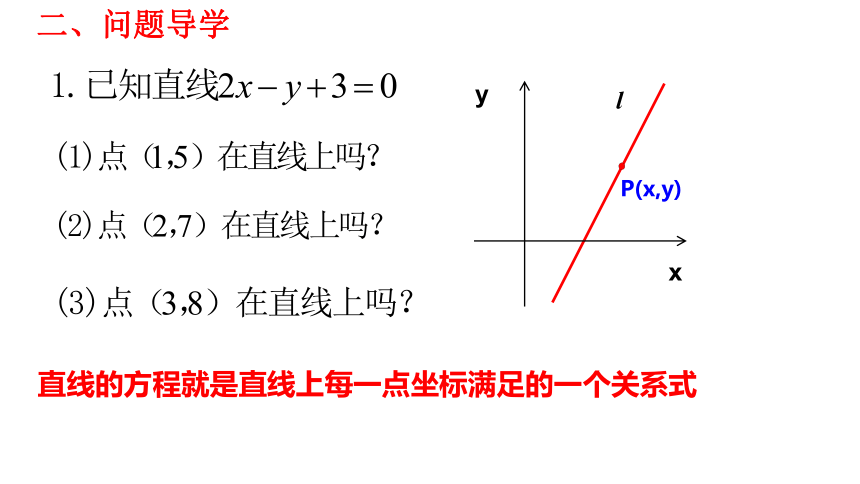
二、问题导学
直线的方程就是直线上每一点坐标满足的一个关系式
y
x
l
P(x,y)
2.思考:
两条直线的交点坐标是下列方程组的解
1.两条直线的交点
几何元素及关系 代数表示
点A
直线l
点A在直线l上
直线l1与l2的交点是A
A的坐标满足方程
A的坐标是方程组的解
三、点拨精讲
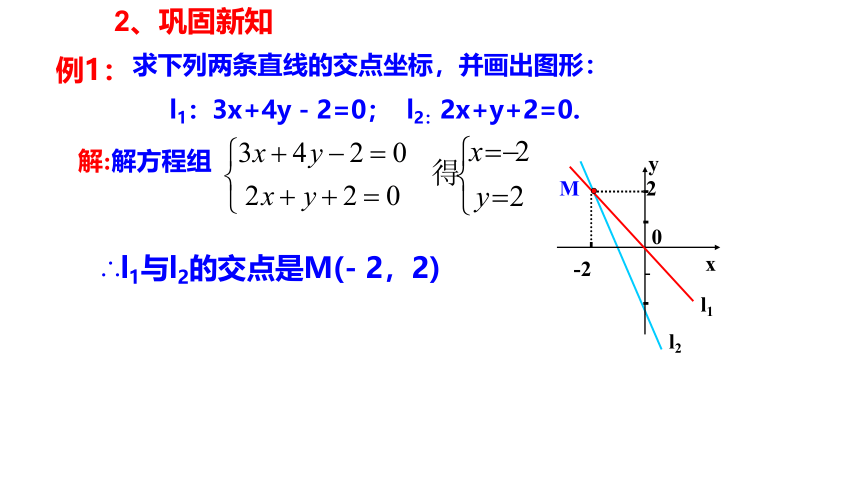
求下列两条直线的交点坐标,并画出图形:
l1:3x+4y-2=0; l2:2x+y+2=0.
解:解方程组
∴l1与l2的交点是M(- 2,2)
x
y
M
-2
2
0
l1
l2
2、巩固新知
例1:
求经过原点且经过以下两条直线的交点的
直线方程: l1:3x+4y-2=0,l2:2x+y+2=0.
设经过原点的直线方程为
y=k x
把(-2,2)代入方程,得k= -1,
所求方程为
y= -x
即 x+y=0
变式练习:
解:解方程组
∴l1与l2的交点是M(- 2,2)
例2:求经过两条直线x+2y-1=0和2x-y-7=0的交点,
且垂直于直线x+3y-5=0的直线方程。
∴这两条直线的交点坐标为(3,-1)
又∵直线x+3y-5=0的斜率是-1/3
∴所求直线的斜率是3
所求直线方程为y+1=3(x-3)即 3x-y-10=0
解法二:所求直线在直线系2x-y-7+λ(x+2y-1)=0中
经整理,可得(2+λ)x+(2λ-1)y-λ-7=0
解得 λ= 1/7
因此,所求直线方程为3x-y-10=0
典型例题
变式练习. 求经过原点且经过以下两条直线的交点的
直线方程: l1:3x+4y-2=0,l2:2x+y+2=0.
例3 判断下列各对直线的位置关系,如果相交,求出其交点的坐标.
(1)
(2)
(3)
解:(1)解方程组
x-y =0
3x+3y-10 = 0
∴l1与l2的交点是M( )
得
例3 判断下列各对直线的位置关系,如果相交,求出其交点的坐标.
(1)
(2)
(3)
解:(2)解方程组
3x-y +4=0 ①
6x-2y-1 = 0 ②
①×2-②得9=0,矛盾,这个方程无解
∴l1与l2的无公共点,l1//l2
例3 判断下列各对直线的位置关系,如果相交,求出其交点的坐标.
(1)
(2)
(3)
解:(3)解方程组
3x+4y -5=0 ①
6x+8y-1 0= 0 ②
①×2得6x+8y-1 0= 0 ,
①和②可以化为同一个方程
∴①和②表示同一条直线,l1与l2重合
四、课堂小结
1.两条直线的交点坐标
2.
过直线A1x+B1y+C1=0和A2x+B2y+C2=0的交点的直线系方程:A1x+B1y+C1+λ(A2x+B2y+C2)=0
五、当堂检测
2.求过两直线x-2y+4=0和x+y-2=0的交点,且满足下列条件的直线l的方程。
(1)过点(2,1)
(2)和直线3x-4y+5=0垂直
(3)和直线2x-y+6=0平行
3.已知a,b满足2a+b=1,则直线ax+3y+b=0必过定
点 .
4.已知直线l1:ax+4y-2=0与直线l2:2x-5y+b=0互相垂直,垂足为(1,c),则a+b+c的值为( )
A.20 B.-4 C.0 D.24
B
5.曲线y=|x|与直线y=kx+1有两个交点,则实数k的取值范围是 .
作业:P79 习题2.3 T2
第二章:直线和圆的方程
2.3.1 :两条直线的交点坐标
数学组:刘华海 吕佩玲
名称
方程的形式
已知条件
方程直线的局限性
一般式
点斜式
斜截式
两点式
截距式
(x1,y1)是直线上一点,k是斜率
k是斜率,b是直线在y轴上的截距
不包括与x轴垂直的直线
a是直线在x轴上的截距,b是直线在y轴上的截距
(x1,y1),(x2,y2)是直线上两点
不包括与x轴垂直的直线
不包括与坐标轴垂直的直线
Ax+By+C=0
(A、B不同时为零)
A、B、C为常数
任何位置的直线
不包括与坐标轴垂直的直线,不包括过原点的直线。
回顾引入
直线方程的五种形式
一、学习目标
1.会用解方程组的方法求两条相交直线的交点坐标.
2.能根据方程组解的个数判断两条直线的位置关系.
3.核心素养:数学运算、直观想象、逻辑推理.
二、问题导学
直线的方程就是直线上每一点坐标满足的一个关系式
y
x
l
P(x,y)
2.思考:
两条直线的交点坐标是下列方程组的解
1.两条直线的交点
几何元素及关系 代数表示
点A
直线l
点A在直线l上
直线l1与l2的交点是A
A的坐标满足方程
A的坐标是方程组的解
三、点拨精讲
求下列两条直线的交点坐标,并画出图形:
l1:3x+4y-2=0; l2:2x+y+2=0.
解:解方程组
∴l1与l2的交点是M(- 2,2)
x
y
M
-2
2
0
l1
l2
2、巩固新知
例1:
求经过原点且经过以下两条直线的交点的
直线方程: l1:3x+4y-2=0,l2:2x+y+2=0.
设经过原点的直线方程为
y=k x
把(-2,2)代入方程,得k= -1,
所求方程为
y= -x
即 x+y=0
变式练习:
解:解方程组
∴l1与l2的交点是M(- 2,2)
例2:求经过两条直线x+2y-1=0和2x-y-7=0的交点,
且垂直于直线x+3y-5=0的直线方程。
∴这两条直线的交点坐标为(3,-1)
又∵直线x+3y-5=0的斜率是-1/3
∴所求直线的斜率是3
所求直线方程为y+1=3(x-3)即 3x-y-10=0
解法二:所求直线在直线系2x-y-7+λ(x+2y-1)=0中
经整理,可得(2+λ)x+(2λ-1)y-λ-7=0
解得 λ= 1/7
因此,所求直线方程为3x-y-10=0
典型例题
变式练习. 求经过原点且经过以下两条直线的交点的
直线方程: l1:3x+4y-2=0,l2:2x+y+2=0.
例3 判断下列各对直线的位置关系,如果相交,求出其交点的坐标.
(1)
(2)
(3)
解:(1)解方程组
x-y =0
3x+3y-10 = 0
∴l1与l2的交点是M( )
得
例3 判断下列各对直线的位置关系,如果相交,求出其交点的坐标.
(1)
(2)
(3)
解:(2)解方程组
3x-y +4=0 ①
6x-2y-1 = 0 ②
①×2-②得9=0,矛盾,这个方程无解
∴l1与l2的无公共点,l1//l2
例3 判断下列各对直线的位置关系,如果相交,求出其交点的坐标.
(1)
(2)
(3)
解:(3)解方程组
3x+4y -5=0 ①
6x+8y-1 0= 0 ②
①×2得6x+8y-1 0= 0 ,
①和②可以化为同一个方程
∴①和②表示同一条直线,l1与l2重合
四、课堂小结
1.两条直线的交点坐标
2.
过直线A1x+B1y+C1=0和A2x+B2y+C2=0的交点的直线系方程:A1x+B1y+C1+λ(A2x+B2y+C2)=0
五、当堂检测
2.求过两直线x-2y+4=0和x+y-2=0的交点,且满足下列条件的直线l的方程。
(1)过点(2,1)
(2)和直线3x-4y+5=0垂直
(3)和直线2x-y+6=0平行
3.已知a,b满足2a+b=1,则直线ax+3y+b=0必过定
点 .
4.已知直线l1:ax+4y-2=0与直线l2:2x-5y+b=0互相垂直,垂足为(1,c),则a+b+c的值为( )
A.20 B.-4 C.0 D.24
B
5.曲线y=|x|与直线y=kx+1有两个交点,则实数k的取值范围是 .
作业:P79 习题2.3 T2
