2.3简谐运动的回复力和能量 课件 (32张PPT)
文档属性
| 名称 | 2.3简谐运动的回复力和能量 课件 (32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-20 09:04:07 | ||
图片预览










文档简介
(共32张PPT)
第二章 机械振动
第3节 简谐运动的回复力和能量
思考并回答问题。
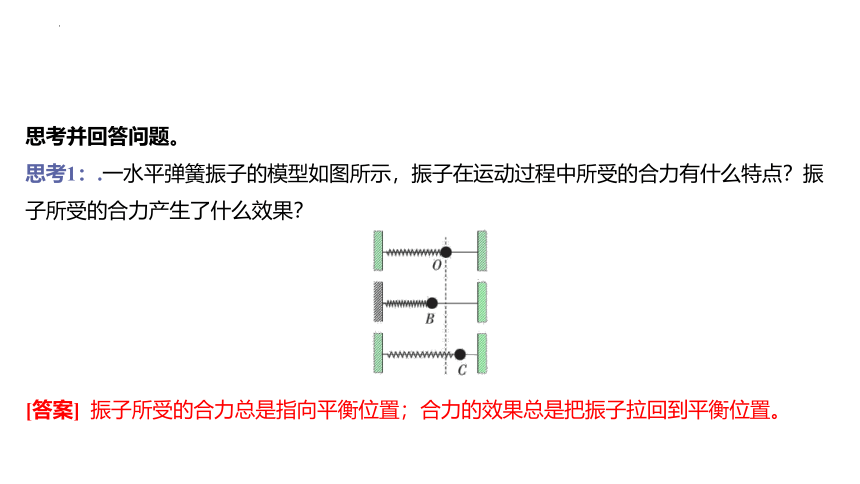
思考1:.一水平弹簧振子的模型如图所示,振子在运动过程中所受的合力有什么特点?振子所受的合力产生了什么效果?
[答案] 振子所受的合力总是指向平衡位置;合力的效果总是把振子拉回到平衡位置。
思考2:.如图所示,一水平弹簧振子在
[答案] 从
正确的打“√”,错误的打“×”。
(1) 简谐运动是一种理想化的振动。( )
√
(2) 回复力的方向总是与位移的方向相反。( )
√
(3) 弹簧振子在关于平衡位置对称的两点,所受回复力相同。( )
×
(4) 弹簧振子位移最大时,动能也最大。( )
×
(5) 弹簧振子运动到平衡位置时,回复力为零,因此能量一定为零。( )
×
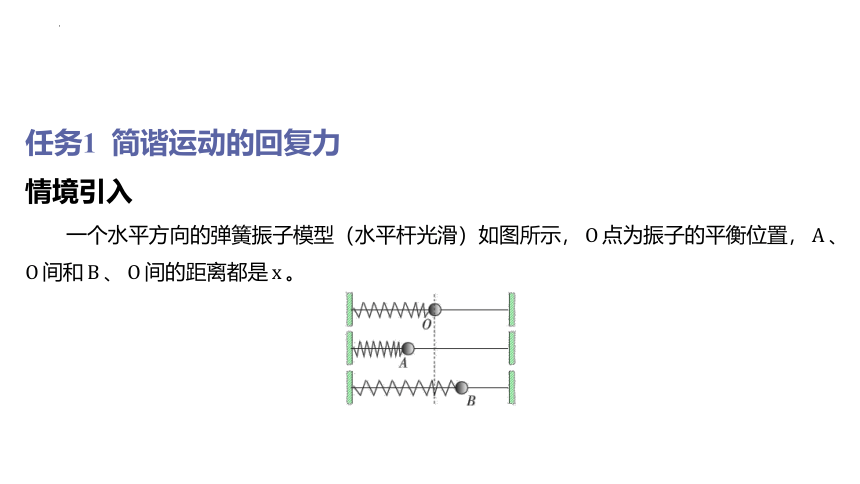
任务1 简谐运动的回复力
情境引入
一个水平方向的弹簧振子模型(水平杆光滑)如图所示,
问题引领
1.振子在
[答案] 两个力。重力、支持力。
2.振子在
[答案] 振子在
3.除重力、支持力、弹簧弹力外,振子在
[答案] 不受。回复力是指将振动的物体拉回到平衡位置的力,是按照力的作用效果来命名的,不是一种新型的力,所以分析物体的受力时,不分析回复力。
回复力可以由某一个力提供(如弹力),也可以是几个力的合力,还可以是某一个力的分力,归纳起来,回复力一定等于物体沿振动方向所受的合力。
知识生成
1.回复力:做简谐运动的物体受到的总能使物体回到①___________的力。
平衡位置
2.简谐运动的动力学特征
(1)回复力的方向跟振子偏离平衡位置的位移方向②_______,总是指向③_______位置,它的作用是使振子能④_______平衡位置。
(2)水平放置的弹簧振子做简谐运动时,其回复力可表示为 ⑤_______,式中 为比例系数,也就是弹簧的⑥___________;负号表示力 与位移 方向相反。
相反
平衡
回到
劲度系数
3.简谐运动
如果质点所受的力的大小与它偏离平衡位置位移的大小成正比,并且该力总是指向平衡位置,质点的运动就是简谐运动。
应用探究
[活动
某水平方向的弹簧振子模型如图所示。当振子离开
[答案] 当离开O点后,受到弹簧的弹力总是指向O点,作为回复力,使其回到平衡位置。简谐运动过程中位移总是偏离平衡位置,由胡克定律可知,使振子回到平衡位置的力与振子离开平衡位置离开平衡位置的位移大小成正比,方向总是指向平衡位置,即与位移方向相反。
[活动
例1 如图所示,劲度系数为
[答案] 见解析
[解析] 设振子的平衡位置为
当弹簧向下发生位移
而回复力
即回复力满足
分析问题.简谐运动的动力学特征是什么
【提示】简谐运动的动力学特征是回复力
证明一个振动为简谐运动的基本思路:
任务2 简谐运动的能量
情境引入
弹簧振子的势能与弹簧的伸长量有关,动能与小球的速度有关。请比较振子在不同位置的能量大小。
问题引领
1.如图所示,仔细分析弹簧振子运动过程中的能量转化情况,请判断各阶段的能量转化情况,并填入表格。
振子的运动
相关量的变化情况 位移大小 _______ _______ _______ _______
速度大小 _______ _______ _______ _______
动能 _______ _______ _______ _______
势能 _______ _______ _______ _______
总能量 _______ _______ _______ _______
减小
增大
减小
增大
增大
减小
增大
减小
增大
减小
增大
减小
减小
增大
减小
增大
不变
不变
不变
不变
2.思考:
(1)弹簧振子在初始释放位置(
(2)弹簧振子在平衡位置时具有什么能?该能量又是如何获得的?
[答案] (1)弹簧振子在初始释放位置(
(2)弹簧振子在平衡位置时具有最大动能,该动能是由势能转化而来的。
知识生成
简谐运动的能量
1.振动系统的状态与能量的关系
振动系统的能量一般指系统的⑦_________。振动的过程就是⑧_______和⑨_______互相转化的过程。
(1)在最大位移处,势能⑩_______,动能 _______。
(2)在平衡位置处,动能 _______,势能 _______。
(3)在简谐运动中,振动系统的机械能 _______,因此简谐运动是一种理想化的模型。
机械能
动能
势能
最大
为零
最大
最小
守恒
2.决定能量大小的因素
振动系统的机械能跟 _______有关, _______越大,机械能就越大,振动越强。一个确定的简谐运动是等幅振动。
振幅
振幅
应用探究
[活动
某水平弹簧振子如图所示,振子在
(1)如果把振子振动的振幅增大,振子回到平衡位置的动能是否增大?振动系统的机械能是否增大?
(2)实际的振动系统中存在空气阻力和摩擦力,能量是否损失?理想化的弹簧振动系统,忽略空气阻力和摩擦力,能量是否损失?
[答案] (1)如果把振子振动的振幅增大,振子回到平衡位置的动能增大,系统的机械能增大。
(2)实际的振动系统,能量逐渐减小;理想化的弹簧振动系统,能量不变。
[活动
例2 把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它围绕平衡位置 在 、 间振动,如图所示,下列结论正确的是( @51@ )。
A
A.小球在
B.小球在
C.小球从
D.小球从
[解析] 小球在平衡位置
分析问题.小球做什么运动?小球从左向右运动的过程中,弹簧的形变量如何变化?
【提示】小球做简谐运动。从左向右运动的过程中,小球的速度先增大后减小;小球从左向右运动的过程中,弹簧的形变量先减小后增大。
如图所示的弹簧振子做简谐运动时,各物理量的变化如下表。
振子的运动
位移 方向 向右 向左 向左 向右
大小 减小 增大 减小 增大
回复力 方向 向左 向右 向右 向左
大小 减小 增大 减小 增大
振子的运动
加速度 方向 向左 向右 向右 向左
大小 减小 增大 减小 增大
速度 方向 向左 向左 向右 向右
大小 增大 减小 增大 减小
振子的动能 增大 减小 增大 减小
弹簧的势能 减小 增大 减小 增大
系统总能量 不变 不变 不变 不变
续表
1.(任务1)(多选)如图所示,物体 与滑块 一起在光滑水平面上做简谐运动, 、 之间无相对滑动。已知轻质弹簧的劲度系数为 , 、 的质量分别为 和 ,重力加速度为 。认为最大静摩擦力等于滑动摩擦力,下列说法正确的是( @54@ )。
ACD
A.物体
B.滑块
C.物体
D.若
[解析] 物体
2.(任务1)公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动但不脱离底板。一段时间内货物在竖直方向上的振动可视为简谐运动,周期为 。取竖直向上为正方向,以某时刻作为计时起点,即 ,其振动图像如图所示,则( @56@ )。
A.
C.
C
[解析] 货物对车厢底板的压力最大时,车厢底板对货物的支持力最大,即货物向上的加速度最大,由振动图像可知
3.(任务2)如图1所示,劲度系数为 的轻弹簧下端挂一质量为 的小球(可视为质点),小球在竖直方向上做简谐运动,弹簧对小球的拉力 随时间变化的图像如图2所示。已知弹簧弹性势能的表达式为 , 为弹簧的形变量,重力加速度为 。下列说法正确的是( @58@ )。
C
A.小球的振幅为
B.小球的最大加速度为
C.小球的最大动能为
D.在振动过程中,弹簧的弹性势能和小球的动能总和不变
[解析] 小球的振幅
4.(任务2)如图所示,一轻质弹簧上端固定,下端悬挂一物块,取物块静止时所处位置为坐标原点 ,向下为正方向,建立 坐标轴。现将物块竖直向下拉到 位置后由静止释放,不计空气阻力。已知物块的质量为 ,弹簧的劲度系数为 ,弹簧弹性势能的表达式为 ( 为弹簧的形变量), 位置的坐标为 ,重力加速度为 。下列说法正确的是( @60@ )。
C
A.该简谐振动的振幅为
B.在任意
C.物块在
D.物块到
[解析] 该简谐振动的振幅为
第二章 机械振动
第3节 简谐运动的回复力和能量
思考并回答问题。
思考1:.一水平弹簧振子的模型如图所示,振子在运动过程中所受的合力有什么特点?振子所受的合力产生了什么效果?
[答案] 振子所受的合力总是指向平衡位置;合力的效果总是把振子拉回到平衡位置。
思考2:.如图所示,一水平弹簧振子在
[答案] 从
正确的打“√”,错误的打“×”。
(1) 简谐运动是一种理想化的振动。( )
√
(2) 回复力的方向总是与位移的方向相反。( )
√
(3) 弹簧振子在关于平衡位置对称的两点,所受回复力相同。( )
×
(4) 弹簧振子位移最大时,动能也最大。( )
×
(5) 弹簧振子运动到平衡位置时,回复力为零,因此能量一定为零。( )
×
任务1 简谐运动的回复力
情境引入
一个水平方向的弹簧振子模型(水平杆光滑)如图所示,
问题引领
1.振子在
[答案] 两个力。重力、支持力。
2.振子在
[答案] 振子在
3.除重力、支持力、弹簧弹力外,振子在
[答案] 不受。回复力是指将振动的物体拉回到平衡位置的力,是按照力的作用效果来命名的,不是一种新型的力,所以分析物体的受力时,不分析回复力。
回复力可以由某一个力提供(如弹力),也可以是几个力的合力,还可以是某一个力的分力,归纳起来,回复力一定等于物体沿振动方向所受的合力。
知识生成
1.回复力:做简谐运动的物体受到的总能使物体回到①___________的力。
平衡位置
2.简谐运动的动力学特征
(1)回复力的方向跟振子偏离平衡位置的位移方向②_______,总是指向③_______位置,它的作用是使振子能④_______平衡位置。
(2)水平放置的弹簧振子做简谐运动时,其回复力可表示为 ⑤_______,式中 为比例系数,也就是弹簧的⑥___________;负号表示力 与位移 方向相反。
相反
平衡
回到
劲度系数
3.简谐运动
如果质点所受的力的大小与它偏离平衡位置位移的大小成正比,并且该力总是指向平衡位置,质点的运动就是简谐运动。
应用探究
[活动
某水平方向的弹簧振子模型如图所示。当振子离开
[答案] 当离开O点后,受到弹簧的弹力总是指向O点,作为回复力,使其回到平衡位置。简谐运动过程中位移总是偏离平衡位置,由胡克定律可知,使振子回到平衡位置的力与振子离开平衡位置离开平衡位置的位移大小成正比,方向总是指向平衡位置,即与位移方向相反。
[活动
例1 如图所示,劲度系数为
[答案] 见解析
[解析] 设振子的平衡位置为
当弹簧向下发生位移
而回复力
即回复力满足
分析问题.简谐运动的动力学特征是什么
【提示】简谐运动的动力学特征是回复力
证明一个振动为简谐运动的基本思路:
任务2 简谐运动的能量
情境引入
弹簧振子的势能与弹簧的伸长量有关,动能与小球的速度有关。请比较振子在不同位置的能量大小。
问题引领
1.如图所示,仔细分析弹簧振子运动过程中的能量转化情况,请判断各阶段的能量转化情况,并填入表格。
振子的运动
相关量的变化情况 位移大小 _______ _______ _______ _______
速度大小 _______ _______ _______ _______
动能 _______ _______ _______ _______
势能 _______ _______ _______ _______
总能量 _______ _______ _______ _______
减小
增大
减小
增大
增大
减小
增大
减小
增大
减小
增大
减小
减小
增大
减小
增大
不变
不变
不变
不变
2.思考:
(1)弹簧振子在初始释放位置(
(2)弹簧振子在平衡位置时具有什么能?该能量又是如何获得的?
[答案] (1)弹簧振子在初始释放位置(
(2)弹簧振子在平衡位置时具有最大动能,该动能是由势能转化而来的。
知识生成
简谐运动的能量
1.振动系统的状态与能量的关系
振动系统的能量一般指系统的⑦_________。振动的过程就是⑧_______和⑨_______互相转化的过程。
(1)在最大位移处,势能⑩_______,动能 _______。
(2)在平衡位置处,动能 _______,势能 _______。
(3)在简谐运动中,振动系统的机械能 _______,因此简谐运动是一种理想化的模型。
机械能
动能
势能
最大
为零
最大
最小
守恒
2.决定能量大小的因素
振动系统的机械能跟 _______有关, _______越大,机械能就越大,振动越强。一个确定的简谐运动是等幅振动。
振幅
振幅
应用探究
[活动
某水平弹簧振子如图所示,振子在
(1)如果把振子振动的振幅增大,振子回到平衡位置的动能是否增大?振动系统的机械能是否增大?
(2)实际的振动系统中存在空气阻力和摩擦力,能量是否损失?理想化的弹簧振动系统,忽略空气阻力和摩擦力,能量是否损失?
[答案] (1)如果把振子振动的振幅增大,振子回到平衡位置的动能增大,系统的机械能增大。
(2)实际的振动系统,能量逐渐减小;理想化的弹簧振动系统,能量不变。
[活动
例2 把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它围绕平衡位置 在 、 间振动,如图所示,下列结论正确的是( @51@ )。
A
A.小球在
B.小球在
C.小球从
D.小球从
[解析] 小球在平衡位置
分析问题.小球做什么运动?小球从左向右运动的过程中,弹簧的形变量如何变化?
【提示】小球做简谐运动。从左向右运动的过程中,小球的速度先增大后减小;小球从左向右运动的过程中,弹簧的形变量先减小后增大。
如图所示的弹簧振子做简谐运动时,各物理量的变化如下表。
振子的运动
位移 方向 向右 向左 向左 向右
大小 减小 增大 减小 增大
回复力 方向 向左 向右 向右 向左
大小 减小 增大 减小 增大
振子的运动
加速度 方向 向左 向右 向右 向左
大小 减小 增大 减小 增大
速度 方向 向左 向左 向右 向右
大小 增大 减小 增大 减小
振子的动能 增大 减小 增大 减小
弹簧的势能 减小 增大 减小 增大
系统总能量 不变 不变 不变 不变
续表
1.(任务1)(多选)如图所示,物体 与滑块 一起在光滑水平面上做简谐运动, 、 之间无相对滑动。已知轻质弹簧的劲度系数为 , 、 的质量分别为 和 ,重力加速度为 。认为最大静摩擦力等于滑动摩擦力,下列说法正确的是( @54@ )。
ACD
A.物体
B.滑块
C.物体
D.若
[解析] 物体
2.(任务1)公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动但不脱离底板。一段时间内货物在竖直方向上的振动可视为简谐运动,周期为 。取竖直向上为正方向,以某时刻作为计时起点,即 ,其振动图像如图所示,则( @56@ )。
A.
C.
C
[解析] 货物对车厢底板的压力最大时,车厢底板对货物的支持力最大,即货物向上的加速度最大,由振动图像可知
3.(任务2)如图1所示,劲度系数为 的轻弹簧下端挂一质量为 的小球(可视为质点),小球在竖直方向上做简谐运动,弹簧对小球的拉力 随时间变化的图像如图2所示。已知弹簧弹性势能的表达式为 , 为弹簧的形变量,重力加速度为 。下列说法正确的是( @58@ )。
C
A.小球的振幅为
B.小球的最大加速度为
C.小球的最大动能为
D.在振动过程中,弹簧的弹性势能和小球的动能总和不变
[解析] 小球的振幅
4.(任务2)如图所示,一轻质弹簧上端固定,下端悬挂一物块,取物块静止时所处位置为坐标原点 ,向下为正方向,建立 坐标轴。现将物块竖直向下拉到 位置后由静止释放,不计空气阻力。已知物块的质量为 ,弹簧的劲度系数为 ,弹簧弹性势能的表达式为 ( 为弹簧的形变量), 位置的坐标为 ,重力加速度为 。下列说法正确的是( @60@ )。
C
A.该简谐振动的振幅为
B.在任意
C.物块在
D.物块到
[解析] 该简谐振动的振幅为
