2.5.2 实验：用单摆测量重力加速度 人教版（2019）选择性必修第一册(共32张PPT)

(共32张PPT)
第二章 机械振动
第5节 实验：用单摆测量重力加速度
第2课时 数据处理与创新
任务1 数据处理
情境引入
通过实验原理我们知道了，单摆的摆长是摆线长度和小球半径之和；实验时使用秒表记录时间。
问题引领
1.该实验使用什么仪器测量单摆的摆长？
[答案] 刻度尺，游标卡尺。
2.该实验使用什么仪器测量单摆的运动周期？
[答案] 秒表。
知识生成
1.怎样测量摆长
方法一： 用刻度尺直接测量小球①_______与悬挂点之间的距离作为摆长的测量值，用图示的方法减小误差。
方法二：用游标卡尺测量小球的②_______，算出它的半径，再测量悬挂点与小球上端之间的距离，以两者之和作为摆长的测量值。
球心
直径
2.如何测量周期
方法一：实验时，可以测量单摆做一次全振动的时间作为它的周期的测量值。
方法二：实验时，测量单摆做多次③_________（例如几十次）的时间，然后通过 ④_ ___求出它的周期的测量平均值。
全振动

应用探究
[活动]读数
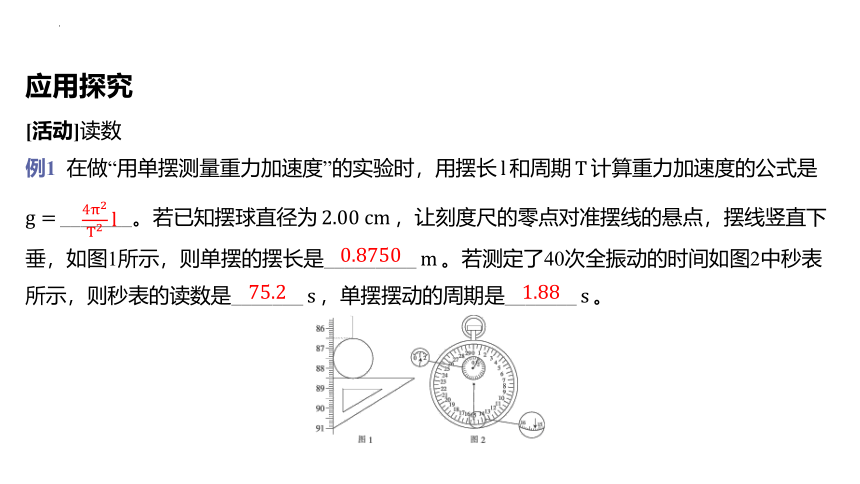
例1 在做“用单摆测量重力加速度”的实验时，用摆长 和周期 计算重力加速度的公式是 _ ______。若已知摆球直径为 ，让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如图1所示，则单摆的摆长是_________ 。若测定了40次全振动的时间如图2中秒表所示，则秒表的读数是_______ ，单摆摆动的周期是_______ 。




[解析] 由 可知
由图可知，摆长
秒表的读数
所以 。
分析问题.（1）图1中摆长怎么计算？
（2）图2中秒表外围的一周是多少秒？最小分度值是多少？
[答案] （1）图1中摆长由最低点的示数减去小球半径得到。（2）图2中秒表外围的一周是 ，最小分度值是 。
任务2 数据分析（含图像）
情境引入
实验过程中有两小组做了下面的实验操作：
小组一：把小球拉到左侧某处由静止释放，同时计时开始，小球再次回到这个位置数数字1，一共数了50次，然后计算周期。
小组二：小球经过最低点开始计时，数数字0，再次回来数数字1，以此类推，一直数到数字100，然后计算周期。
问题引领
1.哪个实验小组对单摆周期的测量更加准确？
[答案] 小组二，可以减小偶然误差。
2.如何计算 ？
[答案] 根据公式 ，可知 ,然后代入数值计算。
知识生成
（1）平均值法：每改变一次摆长，将相应的 和 代入公式中求出 值，最后求出 的平均值。
设计如下所示实验表格。
实验次数 摆长 周期 重力加速度 重力加速度 的平均值
1
2
3
（2） 图像法：由 ⑤_ _______得 ⑥_______，作出⑦________图像，即以 为纵轴，以 为横轴。其斜率 ⑧_ _____，由图像的斜率即可求出重力加速度 的数值。




应用探究
[活动 ]图像法处理数据与误差分析
例2 某同学在实验室利用单摆测量当地的重力加速度。
（1）如图，该同学测出不同摆长 和对应的周期 ，并在坐标纸上作出 图线，由图线可精确求出重力加速度 ___ ___ （已知 ，结果保留3位有效数字）。
9.77
（2）另一同学由单摆周期公式直接求得的 值偏小，则可能是 ______ 。
A.测量悬线长度作为摆长，没有加上摆球的半径
B.把 次全振动误计为 次全振动
C.摆线上端未固定牢，摆动过程中出现松动，使摆线变长
AC
[解析] （1）根据 ，解得 ,根据图像的斜率 ，解得重力加速度 。
（2）根据 ，解得 ，测量悬线长度作为摆长，没有加上摆球的半径，摆长变短，则 值偏小；根据 把 次全振动误计为 次全振动，则测得的周期变小，则 值偏大；摆线上端未固定牢，摆动过程中出现松动，使摆线变长，测得的周期变大，则 值偏小。
分析问题.（1） 图像中图线的斜率表示什么？
（2）从公式上看， 值偏小，可能是哪方面引起的？
[答案] （1）根据单摆的振动周期公式 ，可得 ，则图像的斜率 。
（2）由 可得， 值偏小，可能是因为摆长测短了或周期测大了。
[活动 ]实验创新
例3 某同学用图1所示的装置研究单摆运动的规律。
让摆球在竖直平面内摆动，用力传感器得到细线对摆球拉力 的大小随时间 变化的图线如图2所示，且从最低点开始为计时起点，由图2中所给的数据结合力学规律可得：
（1）该同学先用游标卡尺测量摆球的直径如图3所示，其读数为________ 。
（2）由图像得该单摆的运动周期 ____ 。
（3）摆球的质量 _______ 。
（4）单摆在小角度摆动时的运动可视为简谐振动，因此另一位同学做了“利用单摆装置测定本地的重力加速度”的实验，为了提高实验精度，在实验中改变几次摆线长 并记录相应的周期 ，再以 为横坐标， 为纵坐标，将所得数据连成直线，如图4所示，求得该直线的斜率为 ，则重力加速度 _ _____（用 表示），该同学并未测摆球半径，由图线纵截距 可推知摆球的半径为_ ___（用 、 表示）。





[解析] （1）由图3游标卡尺可知，其读数为 。
（2）当单摆经过最低点时速度最大，细线的拉力最大，一个周期内单摆两次经过最低点，结合图2可知，单摆的运动周期 。
（3）设单摆最大摆角为 ，有 ， ，摆球从最高点运动到最低点，由动能定理得 ，联立解得 。
（4）因为单摆在小角度摆动时可视为简谐振动，由于单摆的周期与重力加速度和摆长之间存在关系 ，可得 ，又因该直线的斜率为 ，即 ，可得重力加速度 ，因为没有测摆球的半径，设摆球的直径为 ，可得周期与摆长的关系为 ，即 ，所以图线截距 ，所以摆球的半径 。
分析问题.（1）图2中的峰值出现的时刻，摆球在最低点还是最高点？相邻峰值之间的时间间隔可以表示什么？
（2）写出图4中图线的表达式。
[答案] （1）最低点；半个周期。（2） 。
1.（任务1）“用单摆测量重力加速度的大小”实验中：
（1） 安装好实验装置后，先用刻度尺测量摆线长 ，再用游标卡尺测量摆球直径 ，其示数如图1所示，则 _______ 。

[解析] 由图1读出 。
（2） 释放摆球，摆动稳定后，从最低点开始计时，并计数为零，此后摆球每次经过最低点依次计数，当数到第60次时停表。此时秒表如图2所示，其读数为_______ ，该单摆的周期 _______ 。


[解析] 秒表如图2所示，其读数 ，单摆的周期 。
（3） 计算重力加速度的表达式为 _ _________（用 、 、 表示）。

[解析] 根据单摆周期公式 ，其中，摆长 ，得 。
2.（任务2）在利用单摆测定重力加速度的实验中：测出不同摆长对应的周期值 ，作出 图像，如图所示， 与 的关系式是 _ ______，利用图线上任两点 、 的坐标 、 可求出图线斜率 ，再由 可求出 _ _______________。


[解析] 根据单摆的周期公式 得， ，可知图线的斜率 ，解得 。
3.（任务2）某同学设计利用如图1所示装置测量重力加速度的大小，传感器固定在悬点 正下方，该传感器可记录光的强弱随时间的变化情况。当小球摆到最低点遮挡光线时，传感器采集的光线最弱，计算机采集数据后得到光的强弱与时间图像如图2所示。
（1） 第1次光最弱到第 次光最弱的时间为 ，则该单摆的周期可表示为 _ _____。（用 、 表示）

[解析] 在一个周期内摆球2次经过平衡位置，一个周期内摆球两次挡光，单摆的周期 。
（2） 该同学用游标卡尺测小球直径 ，如图3所示，则 ________ ，用米尺测量知摆线长为 ，用 、 、 表示重力加速度的公式为 _ _________。


[解析] 用游标卡尺测小球直径 。
单摆摆长 ，单摆周期公式 ，则 。
4.（任务2）某同学在做“利用单摆测重力加速度”的实验。
（1） 下列各项操作正确的是_@44@____。
A.选择有弹性的细线作为摆线
B.从最高位置开始计时
C.选择密度较小的球作为摆球
D.测出小球直径，把单摆固定后，让小球自然下垂，用刻度尺量出摆线的长度，再加上小球的半径作为摆长
D
[解析] 应选择没有弹性的细线作为摆线，A项错误；应从摆球运动到最低点时开始计时，B项错误；应选择密度较大、体积较小的球作为摆球，C项错误；测出小球直径，把单摆固定后，让小球自然下垂，用刻度尺量出摆线的长度，再加上小球的半径，即为摆长，D项正确。
（2） 若测得的重力加速度偏大，则可能是因为_@46@_____。
A.误把悬线长和小球的直径之和作为摆长
B.计算摆长时，只考虑悬线长，漏加了小球的半径
C.测量周期时，将 次全振动误记为 次全振动
D.测量周期时，将 次全振动误记为 次全振动
AC
[解析] 根据 ，可得 ，误把悬线长和小球的直径之和作为摆长，则摆长测量值偏大，得到的 值偏大，A项正确；计算摆长时，只考虑悬线长，漏加了小球的半径，则摆长测量值偏小，得到的 值偏小，B项错误；测量周期时，将 次全振动误记为 次全振动，则周期测量值偏小，得到的 值偏大，C项正确；测量周期时，将 次全振动误记为 次全振动，则周期测量值偏大，则得到的 值偏小，D项错误。
（3） 甲同学准确无误地完成实验，作出了 图像为 ，乙同学也进行了与甲同学同样的实验，但实验后他发现测量摆长时忘了加上摆球的半径，则该同学作出的 图像为图中的_@48@____。
A.虚线①，不平行于实线 B.虚线②，平行于实线
C.虚线③，平行于实线 D.虚线④，不平行于实线
B
[解析] 甲同学准确无误地完成实验，作出了 图像为 ，根据 ，可得 ，摆线长度与摆球半径之和是单摆摆长，测量摆长时忘了加上摆球的半径，摆长测量值小于真实值，即当摆长为零时单摆周期不为零， 图像在纵轴上有截距； 图像的斜率 ，同一位置重力加速度 相同，图像的斜率 相同；由图示图像可知，该同学作出的 图像为虚线②，平行于实线 ，故B项正确， 、 、 三项错误。