一次函数复习公开课[下学期]

课件23张PPT。一次函数复习祯埠乡校 郑明军一次函数：
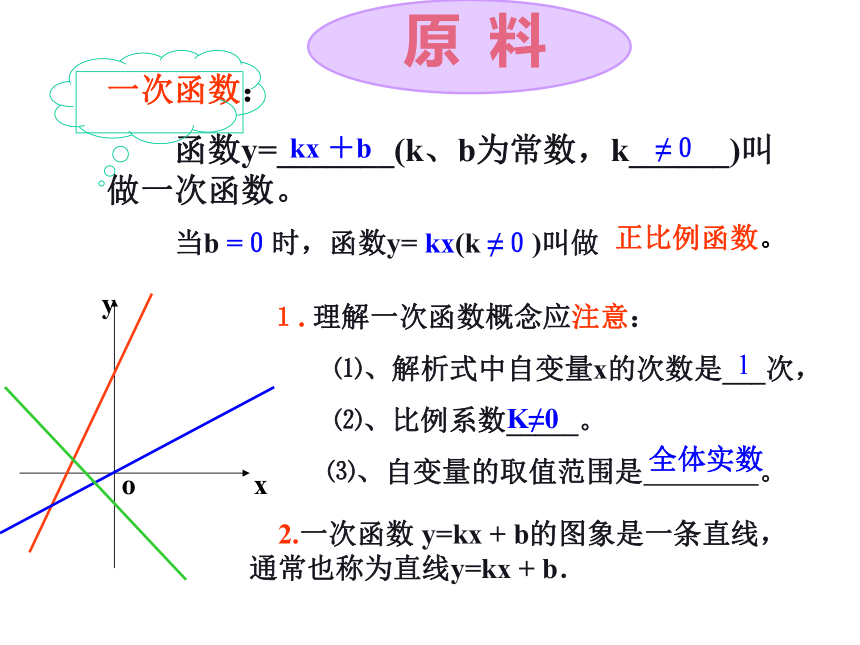
　　函数y=_______(k、b为常数，k______)叫做一次函数。
kx ＋b≠０当b =０时，函数y= kx(k ≠０)叫做
正比例函数。１. 理解一次函数概念应注意：
　　⑴、解析式中自变量x的次数是___次，
⑵、比例系数_____。
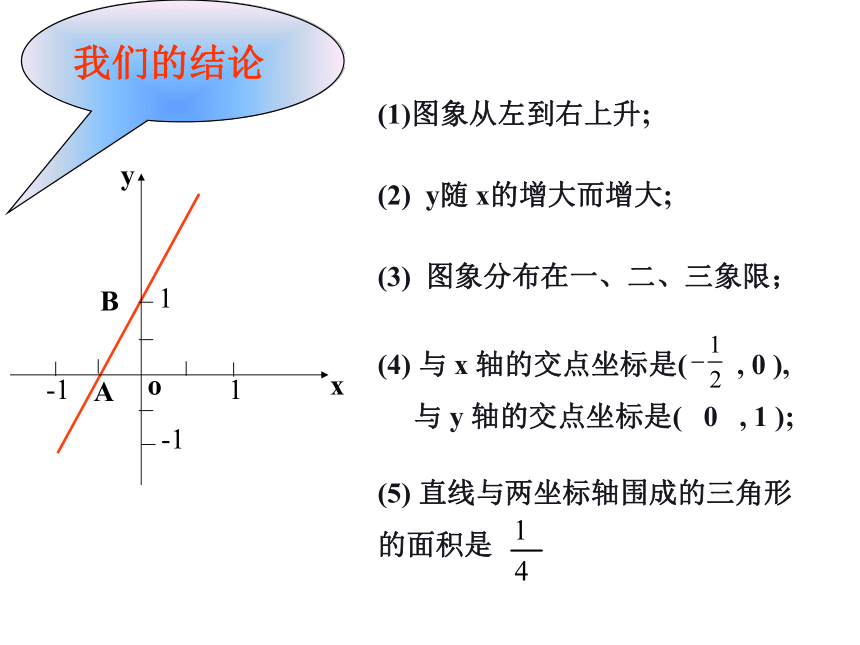
　　⑶、自变量的取值范围是　　　　。1K≠0全体实数　2.一次函数 y=kx + b的图象是一条直线，通常也称为直线y=kx + b．原 料 请画出一次函数y = 2x + 1的图象; 请进一步研究它的图象和性质，尽可能多地说出结论.yAB(1)图象从左到右上升;(2) y随 x的增大而增大;(4) 与 x 轴的交点坐标是( , 0 ),
与 y 轴的交点坐标是( 0 , 1 );(5) 直线与两坐标轴围成的三角形
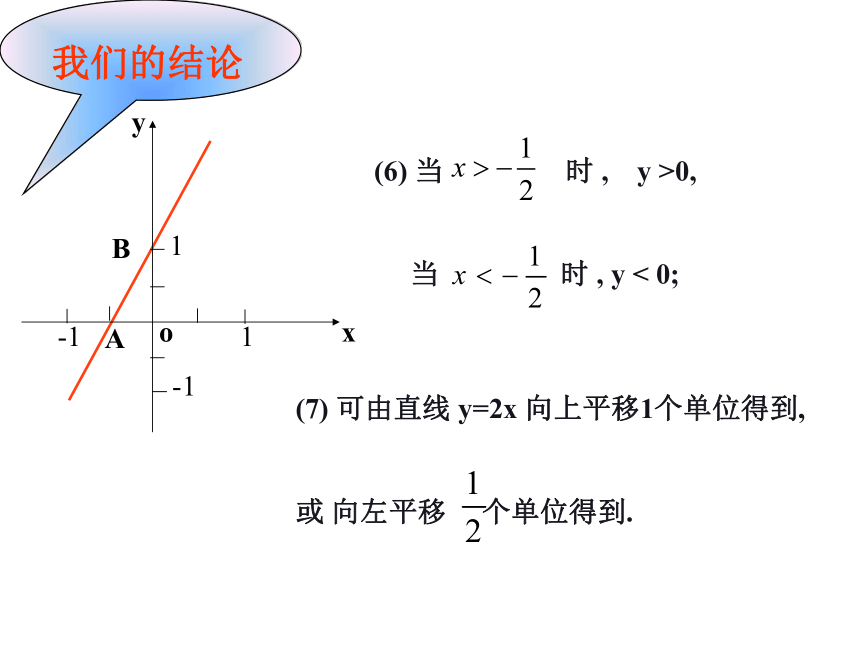
的面积是(3) 图象分布在一、二、三象限；我们的结论 (6) 当 时 , y >0,

当 时 , y < 0;(7) 可由直线 y=2x 向上平移1个单位得到,

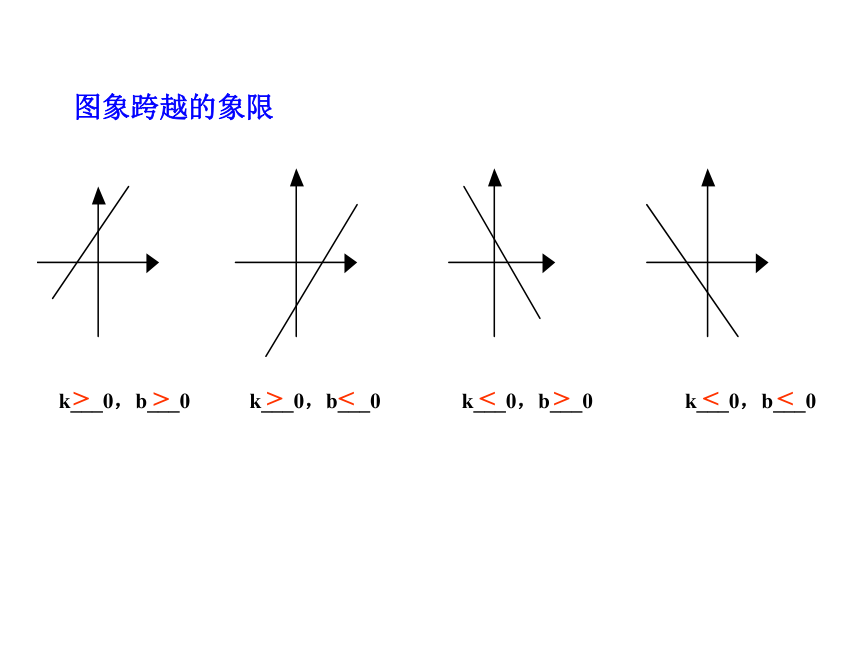
或 向左平移 个单位得到.我们的结论★ k、b 的几何意义k：有关于直线的倾斜方向；b: 有关于直线与y轴的交点； 当 k 相同时，两条直线平行；当 b 相同时，两条直线与 y 轴交于同一点．老师的几点建议：图象跨越的象限k___0，b___0 k___0，b___0 　 k___0，b___0 　　 k___0，b___0<<><<>>>
1、 有下列函数：
①　　　　　 , ②　　　　 ,
③ , ④ 。
其中图象过原点的是_____；
函数y随x的增大而增大的是___________ , 函数y随x的增大而减小的是______；
图象过第一、二、三象限的是_____。②①、②、③④③点 心点 心C2、直线y=2x―4与x轴的交点坐标是 ，与y轴
的交点坐标是 ,直线与两坐标轴围成的三角
形的面积是 。(2,0)( 0, - 4)4点 心4.已知一次函数y=kx+b , y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( 　)
　(A) 　　　　　(B) 　（C） 　　（D）A点 心　5、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（　 　）A点 心 6、一支蜡烛长20厘米，点燃后每小时燃烧5厘米，燃烧时剩下的高度h（厘米）与燃烧时间t（时）的函数关系式的图象是（ ）Dx(吨)y(元)O123456100040005000200030006000 例 l1反映了某公司产品的销售收入与销售量的关系，根据图象回答：l1 (1)当销售量为2吨时，销售收入＝　　　　元，销售收入2000 (2)l1对应的函数表达式是　　　　　　　　，y=1000x小菜一碟x(吨)y(元)O123456100040005000200030006000 (1)当销售成本＝4500元时，销售量＝　　吨；5 l2 反映了该公司产品的销售成本与销售量的
关系， 根据图象回答：销售成本　　(2)l2对应的函数表达式是　　　　　　　　。y=500x+2000x(吨)y(元)O123456100040005000200030006000l1l2（1）当销售量为6吨时，销售收入＝　　　　元，
　　 销售成本＝　　　元， 利润＝　　　　元。60005000销售收入销售成本1000（2）你还能得到什么信息？下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。新龟兔赛跑 s /米（1）这一次是 　米赛跑。12345O10020120406080t /分687（2）表示兔子的图象是 。-11291011-3-2100l2-4根据图象可以知道：s /米（3）当兔子到达终点时，乌龟距终点还有 　米。l1l212345O10020120406080t /分687（4）乌龟要与兔子同时到达终点乌龟要先跑 米。（5）乌龟要先到达终点，至少要比兔子早跑 分钟。-11291011-3-2404-440已知：函数 y = (m+1) x + 2 m﹣6(m≠ -1)
（1）若函数图象过（﹣1 ，2），求此函数的解析式。
（2）若函数图象与直线 y = 2 x + 5 平行，求其函数的解析式。
（3）求满足（2）条件的直线与直线 y = ﹣3 x + 1 的交点,并
求这两条直线 与y 轴所围成的三角形面积 . 解：（1）由题意:
2=﹣(m+1）+2m﹣6解得 m = 9(2) 由题意，m +1= 2
解得 m = 1
∴ y = 2x﹣4(3) 由题意得∴ 这两直线的交点是（1 ，﹣2）y = 2x﹣4 与y 轴交于( 0 , - 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1）●11-4(1, ﹣2)S△=-2∴ y = 10x+12
解得:品龙井 在抗击“禽流感”的过程中,某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后，（1）分别求出0≤ x ≤2 和x>2时y与x之间的函数关系式;
解:(1)当0≤ x ≤2时,设y=k1x(k1≠0)因图象过点(2,6),代入得6=2k1, k1=3∴y=3x当x > 2时, 设y=k2x+b(k2≠0)因图象过点(2,6)及点(10,3),代入得解得抗 “禽流感”（2）如果每毫升血液中含药量为4微克或4微克以上时，治疗疾病有效，那么这个有效时间是多长?
当 0≤ x ≤2时, y=3x;
当x ≥ 2时, 解:当y=4时,由y=3x , 得由 , 得所以使用该种新药的有效时间是６小时．4x1x2? 一路下来，大家收获不小吧！说说你的感受，让大家一起来分享，好吗？…… 今天我们一起回顾了哪些知识？你还有哪些困惑？你对老师有哪些意见和建议？水
果1.结合具体情景体会一次函数的意义；
2.会画一次函数的图象（注意：实际问题中的 图象往往是一条线段，甚至是一些离散的点），掌握一次函数图象的分布规律；
3.能从图象中获取信息（注意弄清楚坐标轴的意义，抓住一些关键性的点）；
4.能结合图象理解一次函数的性质；
5.能用待定系数法求一次函数的解析式；
6.能用一次函数解决一些实际问题。祝同学们学有所获