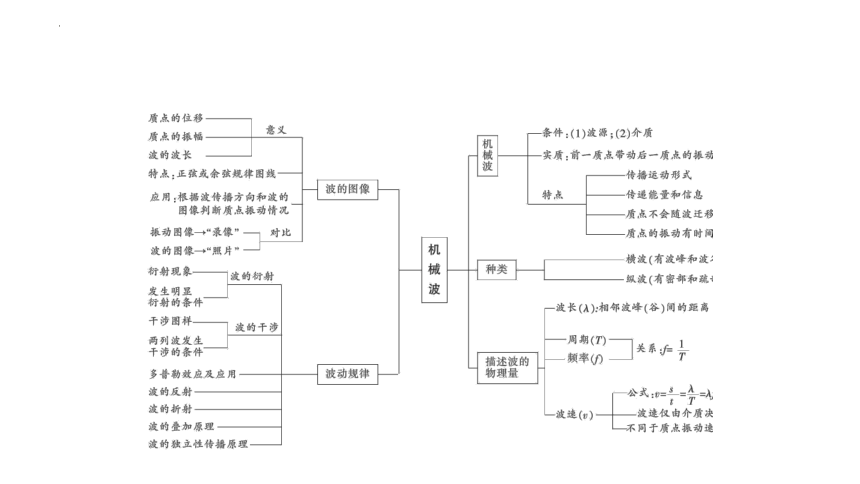
第三章 机械波 整合与提升课件 人教版(2019)选择性必修第一册(共26张PPT)
文档属性
| 名称 | 第三章 机械波 整合与提升课件 人教版(2019)选择性必修第一册(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-20 09:26:18 | ||
图片预览







文档简介
(共26张PPT)
第三章 机械波
第6节 《机械波》整合与提升
任务1 波的形成与传播
机械波的形成实质是介质中的质点间存在相互作用,前面的质点带动后面的质点振动,同时将振动形式和能量向外传播。每一个质点都由前面的质点带动做受迫振动。机械波有如下特点:(1)若不计能量损失,各质点振幅相同;(2)各质点振动周期与波源的振动周期相同,即机械波的频率由波源决定,波速由介质决定;(3)离波源越远,质点振动越滞后,各质点只在各自的平衡位置附近振动,并不随波迁移。
例1 (多选)如图1所示,波源 从平衡位置 开始振动,运动方向竖直向上( 轴的正方向),振动周期 ,产生的简谐波向左、右两个方向传播,波速均为 。经过一段时间后, 、 两点开始振动,已知 、 两点与波源的距离分别为 、 。若以 点开始振动的时刻作为计时起点,则在图2的振动图像中,可能正确描述 、 两点振动情况的是( @1@ )。
A.①为
AD
[解析] 根据波长和波速的关系
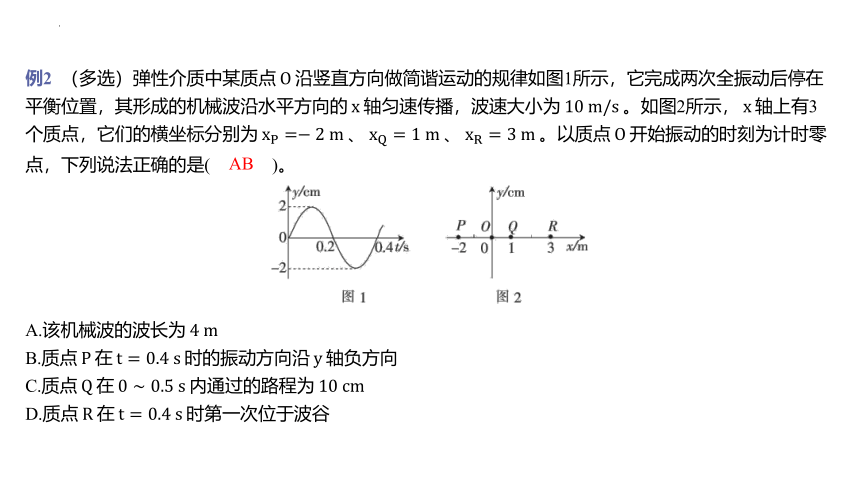
例2 (多选)弹性介质中某质点 沿竖直方向做简谐运动的规律如图1所示,它完成两次全振动后停在平衡位置,其形成的机械波沿水平方向的 轴匀速传播,波速大小为 。如图2所示, 轴上有3个质点,它们的横坐标分别为 、 、 。以质点 开始振动的时刻为计时零点,下列说法正确的是( @3@ )。
A.该机械波的波长为
B.质点
C.质点
D.质点
AB
[解析] 由图1可知,波的周期
机械波的形成与传播规律
(1)机械波传播的只是振动的形式和能量,质点只在各自的平衡位置附近做简谐运动,并不随波迁移。
(2)介质中各质点的振幅相同,振动周期和频率都与波源的振动周期和频率相同。
(3)沿波的传播方向,各质点的振动依次落后,且后面的质点总是重复前面质点的振动。波传播到任意一点时,该点的起振方向都和波源的起振方向相同。
(4)波从一种介质进入另一种介质,由于介质不同,它的波长和波速可能改变,但频率和周期都不会改变。
(5)波速
(6)相隔波长整数倍的两质点,振动状态总相同;相隔半波长奇数倍的两质点,振动状态总相反。波上质点振动
任务2 波动与振动的综合
波动是若干个质点振动的宏观表现,而每个质点的振动是波动的微观本质。所以波动与质点的振动之间存在内在的联系,要学会从三个角度去分析波动问题:(1)波动规律:波在同一介质中匀速传播,
例3 (多选)图1为一列简谐横波在 时刻的波形图, 是平衡位置 处的质点, 是平衡位置 处的质点,图2为质点 的振动图像,则( @5@ )。
A.横波的波长是
C.质点
AD
[解析] 由波的图像可知,横波的波长是
遇到波的图像和振动图像问题时分析的一般步骤:
(1)先看两轴。由两轴确定图像种类。
(2)读取直接信息。从振动图像上可直接读取周期和振幅;从波的图像上可直接读取波长和振幅。
(3)读取间接信息。利用振动图像可确定某一质点在某一时刻的振动方向;再利用波的图像可进行波传播方向与某一质点振动方向的互判。
(4)利用波速关系式。波长、波速、周期、频率间一定满足
例4 一列简谐横波在
(1)求此列波的波速大小,并说明质点
(2)画出
[答案] (1)
[解析] (1)由图1知波长
(2)
任务3 波动问题的多解性
波在传播过程中,由于空间周期性、时间周期性和传播方向的双向性而引起多解,解决这类问题要注意下列情况:
1.波的空间周期性。在波的传播方向上,相距为波长整数倍的质点的振动情况相同。
2.波的时间周期性。由波的传播特性可知,经过整数倍个周期,波的图像相同。
3.波的传播方向的双向性。若根据题中条件无法确定波的传播方向,在解题时要注意考虑波的传播方向可能有两个方向。
例5 如图所示,实线是一列简谐横波在
(1)若这列波的周期
(2)若波速大小为
[答案] (1)沿
(2)沿
[解析] (1)①当波沿
②当波沿
(2)波速大小为
机械波问题的一个特点是多解性。它一般分为
例6 一列简谐横波沿直线由 向 传播,相距 的 、 两处的质点振动图像如图中 、 所示,则( @11@ )。
A.该波的振幅是
C.该波的波速可能是
B
[解析] 由题图读出,该波的振幅
任务4 波的特性
波在同一均匀介质中沿直线匀速传播;而在不同介质中传播时,由于波速发生了变化,所以发生折射现象; 当波遇到障碍物时,如果障碍物的尺寸小于波长或与波长差不多时,表现为明显衍射,如果障碍物的尺寸大于波长时,表现为反射。在一列波与另一列波相遇时,会发生波的叠加,相遇后仍保持原有的运动特性;而一列波与另一列频率相同、相位差恒定的波相遇时,会产生干涉现象。当波源与观察者之间存在相对运动时,会观察到多普勒效应。波的衍射与干涉是波特有的性质;在今后的电磁波的学习中仍十分重要。
例7 (多选)两列相干水波某时刻的波峰和波谷位置如图所示,实线表示波峰,虚线表示波谷,相邻实线与虚线间的距离为 ,波速为 ,在图示范围内可以认为这两列波的振幅均为 , 点是相邻实线与虚线间的中点,则( @13@ )。
A.图示时刻
B.图示时刻
C.
D.经
BC
[解析]
理解波的干涉现象要注意:
(1)频率相同的两列波叠加,使某些区域的振动加强,某些区域的振动减弱,并且产生振动加强和振动减弱的区域相互间隔的现象。
(2)产生稳定干涉现象的条件是两列波的频率相同,相位差保持不变。
(3)稳定干涉中,振动加强区域或振动减弱区域的空间位置是不变的。加强区域中心质点的振幅等于两列波的振幅之和;减弱区域中心质点的振幅等于两列波的振幅之差的绝对值。
(4)加强区永远是加强区,减弱区永远是减弱区,描述振动强弱的物理量是振幅,而振幅不是位移。每个质点在振动过程中的位移是在不断改变的,但振幅是保持不变的,所以振动最强的点无论处于波峰还是波谷,振动始终是最强的。加强区内各质点的振动位移不一定都比减弱区内各点的振动位移大。
第三章 机械波
第6节 《机械波》整合与提升
任务1 波的形成与传播
机械波的形成实质是介质中的质点间存在相互作用,前面的质点带动后面的质点振动,同时将振动形式和能量向外传播。每一个质点都由前面的质点带动做受迫振动。机械波有如下特点:(1)若不计能量损失,各质点振幅相同;(2)各质点振动周期与波源的振动周期相同,即机械波的频率由波源决定,波速由介质决定;(3)离波源越远,质点振动越滞后,各质点只在各自的平衡位置附近振动,并不随波迁移。
例1 (多选)如图1所示,波源 从平衡位置 开始振动,运动方向竖直向上( 轴的正方向),振动周期 ,产生的简谐波向左、右两个方向传播,波速均为 。经过一段时间后, 、 两点开始振动,已知 、 两点与波源的距离分别为 、 。若以 点开始振动的时刻作为计时起点,则在图2的振动图像中,可能正确描述 、 两点振动情况的是( @1@ )。
A.①为
AD
[解析] 根据波长和波速的关系
例2 (多选)弹性介质中某质点 沿竖直方向做简谐运动的规律如图1所示,它完成两次全振动后停在平衡位置,其形成的机械波沿水平方向的 轴匀速传播,波速大小为 。如图2所示, 轴上有3个质点,它们的横坐标分别为 、 、 。以质点 开始振动的时刻为计时零点,下列说法正确的是( @3@ )。
A.该机械波的波长为
B.质点
C.质点
D.质点
AB
[解析] 由图1可知,波的周期
机械波的形成与传播规律
(1)机械波传播的只是振动的形式和能量,质点只在各自的平衡位置附近做简谐运动,并不随波迁移。
(2)介质中各质点的振幅相同,振动周期和频率都与波源的振动周期和频率相同。
(3)沿波的传播方向,各质点的振动依次落后,且后面的质点总是重复前面质点的振动。波传播到任意一点时,该点的起振方向都和波源的起振方向相同。
(4)波从一种介质进入另一种介质,由于介质不同,它的波长和波速可能改变,但频率和周期都不会改变。
(5)波速
(6)相隔波长整数倍的两质点,振动状态总相同;相隔半波长奇数倍的两质点,振动状态总相反。波上质点振动
任务2 波动与振动的综合
波动是若干个质点振动的宏观表现,而每个质点的振动是波动的微观本质。所以波动与质点的振动之间存在内在的联系,要学会从三个角度去分析波动问题:(1)波动规律:波在同一介质中匀速传播,
例3 (多选)图1为一列简谐横波在 时刻的波形图, 是平衡位置 处的质点, 是平衡位置 处的质点,图2为质点 的振动图像,则( @5@ )。
A.横波的波长是
C.质点
AD
[解析] 由波的图像可知,横波的波长是
遇到波的图像和振动图像问题时分析的一般步骤:
(1)先看两轴。由两轴确定图像种类。
(2)读取直接信息。从振动图像上可直接读取周期和振幅;从波的图像上可直接读取波长和振幅。
(3)读取间接信息。利用振动图像可确定某一质点在某一时刻的振动方向;再利用波的图像可进行波传播方向与某一质点振动方向的互判。
(4)利用波速关系式。波长、波速、周期、频率间一定满足
例4 一列简谐横波在
(1)求此列波的波速大小,并说明质点
(2)画出
[答案] (1)
[解析] (1)由图1知波长
(2)
任务3 波动问题的多解性
波在传播过程中,由于空间周期性、时间周期性和传播方向的双向性而引起多解,解决这类问题要注意下列情况:
1.波的空间周期性。在波的传播方向上,相距为波长整数倍的质点的振动情况相同。
2.波的时间周期性。由波的传播特性可知,经过整数倍个周期,波的图像相同。
3.波的传播方向的双向性。若根据题中条件无法确定波的传播方向,在解题时要注意考虑波的传播方向可能有两个方向。
例5 如图所示,实线是一列简谐横波在
(1)若这列波的周期
(2)若波速大小为
[答案] (1)沿
(2)沿
[解析] (1)①当波沿
②当波沿
(2)波速大小为
机械波问题的一个特点是多解性。它一般分为
例6 一列简谐横波沿直线由 向 传播,相距 的 、 两处的质点振动图像如图中 、 所示,则( @11@ )。
A.该波的振幅是
C.该波的波速可能是
B
[解析] 由题图读出,该波的振幅
任务4 波的特性
波在同一均匀介质中沿直线匀速传播;而在不同介质中传播时,由于波速发生了变化,所以发生折射现象; 当波遇到障碍物时,如果障碍物的尺寸小于波长或与波长差不多时,表现为明显衍射,如果障碍物的尺寸大于波长时,表现为反射。在一列波与另一列波相遇时,会发生波的叠加,相遇后仍保持原有的运动特性;而一列波与另一列频率相同、相位差恒定的波相遇时,会产生干涉现象。当波源与观察者之间存在相对运动时,会观察到多普勒效应。波的衍射与干涉是波特有的性质;在今后的电磁波的学习中仍十分重要。
例7 (多选)两列相干水波某时刻的波峰和波谷位置如图所示,实线表示波峰,虚线表示波谷,相邻实线与虚线间的距离为 ,波速为 ,在图示范围内可以认为这两列波的振幅均为 , 点是相邻实线与虚线间的中点,则( @13@ )。
A.图示时刻
B.图示时刻
C.
D.经
BC
[解析]
理解波的干涉现象要注意:
(1)频率相同的两列波叠加,使某些区域的振动加强,某些区域的振动减弱,并且产生振动加强和振动减弱的区域相互间隔的现象。
(2)产生稳定干涉现象的条件是两列波的频率相同,相位差保持不变。
(3)稳定干涉中,振动加强区域或振动减弱区域的空间位置是不变的。加强区域中心质点的振幅等于两列波的振幅之和;减弱区域中心质点的振幅等于两列波的振幅之差的绝对值。
(4)加强区永远是加强区,减弱区永远是减弱区,描述振动强弱的物理量是振幅,而振幅不是位移。每个质点在振动过程中的位移是在不断改变的,但振幅是保持不变的,所以振动最强的点无论处于波峰还是波谷,振动始终是最强的。加强区内各质点的振动位移不一定都比减弱区内各点的振动位移大。
