一次函数应用专题[上学期]

课件10张PPT。《函数的应用专题》
（1）小明全家在旅游景点游玩了多少小时？
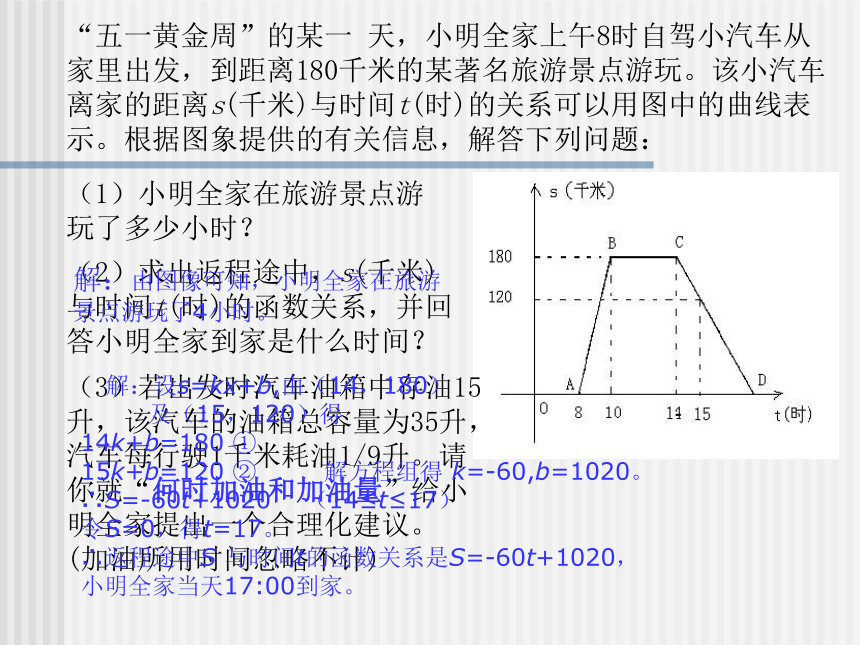
“五一黄金周”的某一 天，小明全家上午8时自驾小汽车从家里出发，到距离180千米的某著名旅游景点游玩。该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示。根据图象提供的有关信息，解答下列问题：（2）求出返程途中，s(千米)与时间t(时)的函数关系，并回答小明全家到家是什么时间？（3）若出发时汽车油箱中存油15升，该汽车的油箱总容量为35升，汽车每行驶1千米耗油1/9升。请你就“何时加油和加油量”给小明全家提出一个合理化建议。 (加油所用时间忽略不计)解：由图像可知，小明全家在旅游 　　景点游玩了4小时。 解：设s=kx+b,由（14，180）
及（15，120）得
14k+b=180 ①
15k+b=120 ② 解方程组得 k=-60,b=1020。
∴S=-60t+1020 （14≤t≤17）
令S=0，得t=17。
∴返程途中S 与时间t的函数关系是S=-60t+1020，
小明全家当天17:00到家。
（3）本题答案不唯一，只要合理即可，但需注意合理性， 主要体现在：
①9:30前必须加一次油；
②若8:30前将油箱加满，则当天在油用完前的适当时 间必须第二次加油；
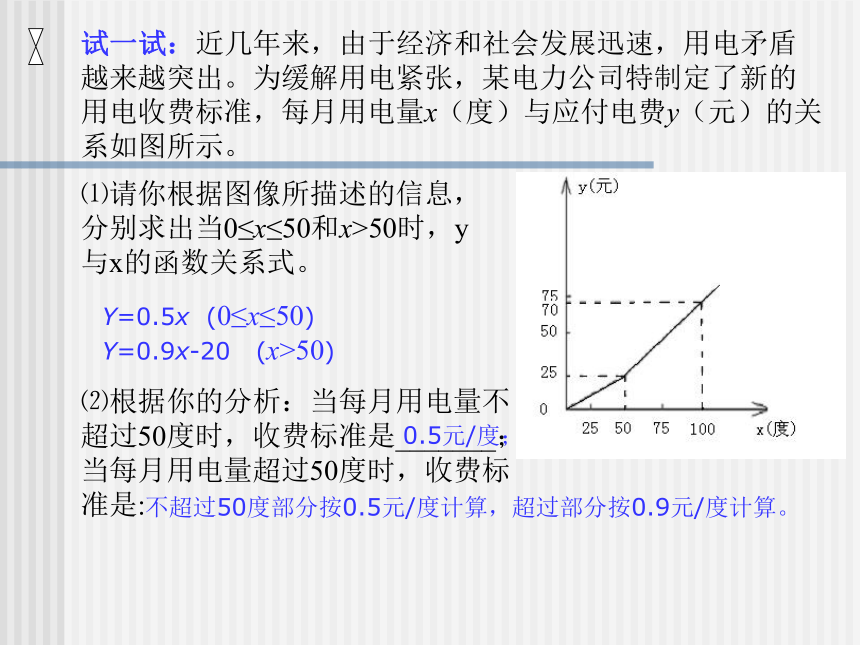
③全程可多次加油，但加油总量至少为25升。⑴请你根据图像所描述的信息，分别求出当0≤x≤50和x>50时，y与x的函数关系式。⑵根据你的分析：当每月用电量不超过50度时，收费标准是_______；当每月用电量超过50度时，收费标准是:Y=0.5x (0≤x≤50)
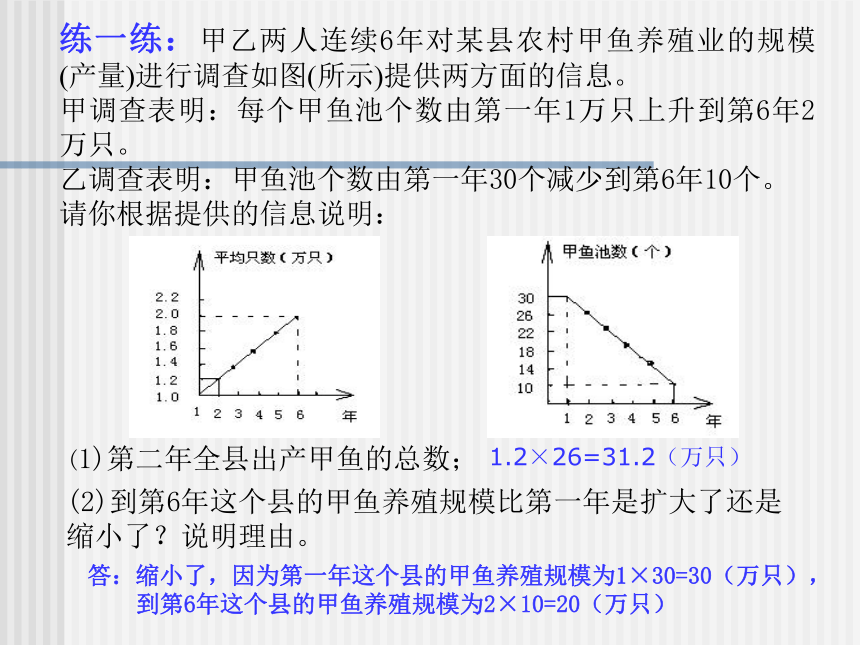
Y=0.9x-20 (x>50)不超过50度部分按0.5元/度计算，超过部分按0.9元/度计算。0.5元/度；(1)第二年全县出产甲鱼的总数；(2)到第6年这个县的甲鱼养殖规模比第一年是扩大了还是缩小了？说明理由。1.2×26=31.2（万只）　　答：缩小了，因为第一年这个县的甲鱼养殖规模为1×30=30（万只），
到第6年这个县的甲鱼养殖规模为2×10=20（万只）　　（注：运费单价表示每平方米草皮运送1千米所需的人民币。）探究：为了美化校园环境，争创绿色学校，某县教育局委托园林公司对A、B两校进行校园绿化。已知A校有如图1的阴影部分空地需铺设草坪，B校有如图2的阴影部分空地需铺设草坪。在甲、乙两地分别有同种草皮3500平方米和2500平方米出售，且售价一样。若园林公司向甲、乙两地购买草皮，其路程和运费单价表如下：求(1)分别求出图1、图2的阴影 　　　部分面积；(3)请设计总运费最省的草皮运送方案，并说明理由。解:SA=(92-2)(42-2)=3600米2
SB=(62-2)×40=2400米2(2)请你给出一种草皮运送方案， 并求出总运费；(3)设甲地运往A校的草皮为x平方米，总运费为y元。∴甲地运往B校的草皮为(3500- x)平方米，
乙地运往A校的草皮为(3600- x)平方米，
乙地运往B校的草皮为(x -1100)平方米。∴ y=20×0.15 x +10×0.15(3500- x)+15×0.2(3600- x) +20×0.2(x -1100)=2.5 x +11650∵ x ≥0,3500- x ≥0,3600- x ≥0,x -1100≥0.∴1100≤ x≤3500由于一次函数y=2.5x+11650的值y是随x的增大而增大的，
所以当x=1100时y取得最小值，即
y=2.5×1100 +11650=14400 (元)总运费最省的方案为：［练一练］
某工厂生产某种产品，每件产品的出厂价为50元，其成本价为25元，因为在生产过程中，平均每生产一件产品有0.5立方米污水排出，所以为了净化环境，工厂设计两种对污水进行处理的方案，并准备实施。
方案1:工厂将污水先并净化处理后排出,每处理1立方米污水，所用的原料费为2元,并且每月排污设备损耗费为30000元。
方案2:工厂将污水排放到污水厂统一处理，每处理1立方米污水需付14元的处理费。⑴设工厂每月生产x件产品，每月利润为y元，分别求出施行方案1和方案2时，y与x的函数关系式;(利润＝总收入－总支出)⑵月生产量为6000件产品时，在不污染环境双节约资金的前提下应选哪种处理污水的方案？请通过计算加以说明。Y1=(50-25) x -0.5× x × 2 -30000=24 x -30000
Y2=(50-25) x -0.5 × x × 14 =18 xY1=24 x -30000=24×6000-30000=114000元
Y2=18 x =18×6000=108000元本课的全过程可以概括为：（3）数学与生活、生产实际有密切联系，我们碰到实际问题要善于用数学方法去分析、去解决，看到数学的函数图像也要善于给它赋予不同的意义，这是学好数学的秘诀之一。（1）识别、分析函数图表所描述的信息；探究性作业
（1）适当选取【问题1】图象中所给的数据，编一个一元一次方程的应用题，并列出方程（不用求解方程）。
（2）请你联系生活、生产实际，也可联系其他学科的知识，给【问题1】图象赋予不同的意义，提出两个以上意义不同的问题。