函数、一次函数[下学期]

课件30张PPT。浙江省衢州华茂外国语学校 余金耀初三数学总复习（ 函数部分 ）2006中考考试目标21.函数及其表示法
(1)了解常量、变量的意义; a
(2)了解函数的概念和三种表示法; a
(3)能结合图像对简单实际问题中的函数关系进行分析; c
23.函数关系及其意义
(1)能用适当的函数表示法刻画某些实际问题中变量之间的关系; c
(2)结合对函数关系的分析，尝试对变量的变化规律进行初步预测c
(3)探索具体问题中的数量关系和变化规律 c22.函数值、函数的自变量取值范围
(1)能确定简单的整式、分式和简单实际问题中的函数的
自变量取值范围; c
(2)会求函数值 c一、常量与变量
1.常量与变量：
在某一变化过程中，不断变化的数量叫变量.在某一变化过程中保持不变的量叫常量.
2.变量之间的关系:
在某一变化中,如果一个变量 Y随着另一个变量 X的变化而不断变化,那么X叫自变量,Y叫因变量.

1. 意义:
设在一个变化过程中有两个变量 x与y , 如果对于x的每一个值 , y 都有唯一的值与它 对应 , 就说x是自变量 , y是x的函数. 2.表示法:
(1)解析法(自变量的取值范围).
(2)列表法.
(3)图象法(图象的画法).二. 函 数： 三、函数表示方法
解析法:用一个式子表示函数关系;
列表法:用列表的方法表示函数关系;
图象法:用图象的方法表示函数关系.变量间关系简捷明了,便于分析计算.需要通过计算,才能得到所需结果.能直接得到某些具体的对应值不能反映函数整体的变化情况直观表示了变量间变化过程和变化趋势.函数值只能是近似值..表达式是基础,是重点,表格是画图象的关键,图象是在表达式和表格的基础上对函数的总体概括和形象化的表达.四、一次函数：　　1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。kx ＋b≠０ = ０≠０kx★理解一次函数概念应注意下面两点：
　　⑴、解析式中自变量x的次数是___次，
⑵、比例系数_____。1K≠0 　　2、正比例函数y=kx(k≠0)的图象是过点（_____），(______)的_________。
　　 3、一次函数y=kx+b(k≠0)的图象是过点（0，___),（____，0)的__________。0，01，k 一条直线b一条直线4、正比例函数y=kx（k≠0)的性质：
　　⑴当k>0时，图象过______象限；y随x的增大而____。
　　⑵当k<0时，图象过______象限；y随x的增大而____。一、三 增大 二、四 减小 5、一次函数y=kx+b(k ≠ 0)的性质：
　　⑴当k>0时，y随x的增大而_________。
　　⑵当k<0时，y随x的增大而_________。
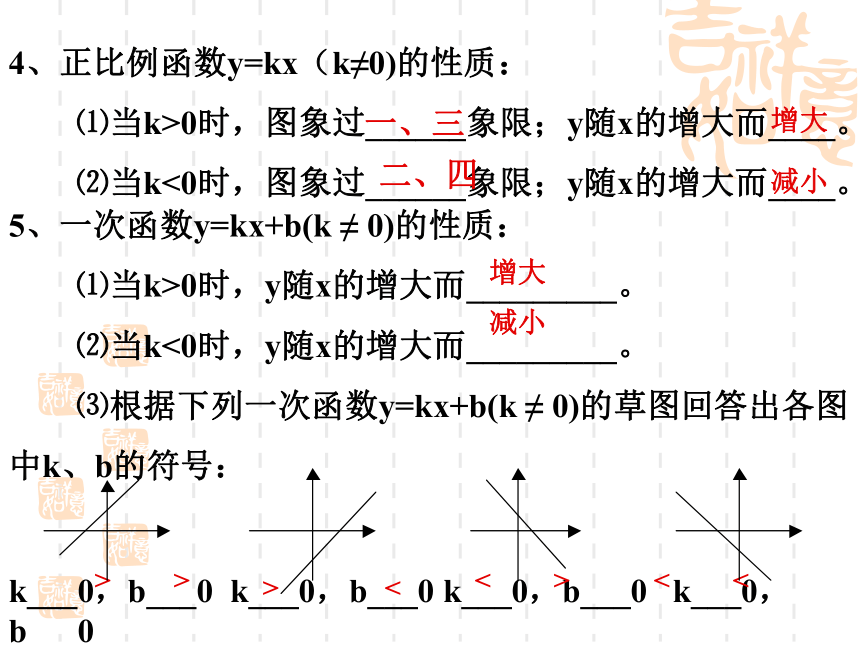
　　⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
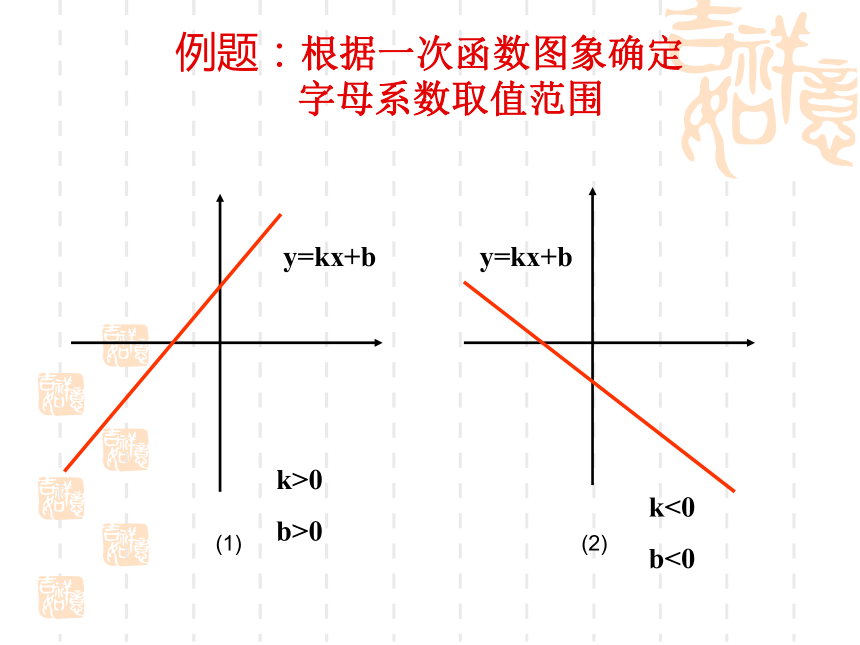
中k、b的符号：增大 减小 k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0<<><<>>>例题：根据一次函数图象确定 字母系数取值范围k>0
b>0k<0
b<0总结：你是如何根据一次函数图象确定k、b取值范围的（1）由一次函数图象的增减性确定k的取值
a.增函数，即y随x的增大而增大
（直观看直线上升，过一三象限）
→ k>0b.减函数，即y随x的增大而减小
（直观看直线下降，过二四象限）
→ k<0（2）由直线和y轴的交点确定b的取值因为直线y=kx+b与y轴交点坐标为（0，b) ，所以1.当直线交y轴正半轴时→ b>02.当直线交y轴负半轴时→ b<0(0,b)(0,b)3.当直线经过原点时→ b=0根据你所学知识，确定下列一次函数中字母系数的取值范围y=kx+by=kx+by=(5-a)x+c+3y=-ax-b根据你所学知识，确定下列一次函数中字母系数的取值范围y=(5-a)x+b+3y=(k-2)x-b(3)(4)OxxyyO六、一次函数,一元一次方程,一元一次不等式(1)当y=0时,为一元一次方程kx+b=0,这时方程的解为:(2)当y>0时,为一元一次不等式kx+b>0;当y<0时,为一元一次不等式kx+b<0.这时不等式的解集分别为:一次函数,一元一次方程,一元一次不等式的关系Y=0 ·二、范例。
例１　填空题：
(1)　有下列函数：①　　　　　 , ②　　　　 ,
③　　　 , ④ 。其中过原点的直
线是_____；函数y随x的增大而增大的是___________；函数y随x的增大而减小的是______；图象在第一、二、三象限的是_____。②①、②、③④③　　(2)、如果一次函数y=kx-3k+6的图象经过原点，那么k的值为________。
　　(3)、已知y-1与x成正比例，且x=－2时，y=4，那么y与x之间的函数关系式为_________________。
k=21、设函数表达式；
2、根据已知条件列出有关k、b的方程；
3、解方程，求k、b；
4、把k、b回代到表达式中，写出明朗化的表达式。解：一次函数当x=1时，y=5。且它的图象与x轴交点
是（６，０）。由题意得解得∴一次函数的解析式为　y= - x+6。点评：用待定系数法求一次函数y=kx+b的解析式，可由已知条件给出的两对x、y的值，列出关于k、b的二元一次方程组。由此求出k、b的值，就可以得到所求的一次函数的解析式。例２、已知一次函数y=kx+b(k≠0)在x=1时，y=5，且它的图象与x轴交点的横坐标是６，求这个一次函数的解析式。 　　例３　柴油机在工作时油箱中的余油量Q(千克）与工作时间t（小时）成一次函数关系，当工作开始时油箱中有油40千克，工作3.5小时后，油箱中余油22.5千克(1)写出余油量Q与时间t的函数关系式；（2）画出这个函数的图。解：（１）设Ｑ＝kt＋b。把t=0，Q=40；t=3.5 ，Q=22.5
分别代入上式，得解得解析式为：Q＝－５t+40　　(0≤t≤8)（２）、取t=0，得Q=40；取t=８，得Q=０。描出点Ａ（０，40），B（8，0）。然后连成线段AB即是所求的图形。点评：（1）求出函数关系式时，
必须找出自变量的取值范围。
（2）画函数图象时，应
根据函数自变量的取值范围来
确定图象的范围。20图象是包括
两端点的线段..AB例4 已知一次函数(1) k为何值时,它的图象经过原 点(2)k 为何值时,它的图象经过点(0, —2)(3)k 为何值时,它的图象平行直线 y=— x(4) k为何值时,它的图象向下平移后,
变成直线y=2x+8(5)k 为何值时, y随x的增大而 减 小例5已知函数(1)当x=0时, y =(2 )当x=5时, y=
(3)当y=0时, x=
(4)当y＞0时, x的取值范围 是(6)当－1≤y≤1时, x的取值范围 是(5)当y＜0.5 时, x的取值范围是-0.52.5例6 已知直线 y=2x－4 (1)求直线关于x轴对称的函数关系式 (3)求直线绕原点旋转1800时的函数关系式(2)求直线关于y轴对称的函数关系式y= － 2x+4y= － 2x- 4
y= 2x+4
1 一次函数 Y=3x+b 的图象与两坐标轴围成的三角形的面积为48,求b的值.:2 设点P(3,m),Q(n,2)都在函数y=x+b的图象上,
求m+n的值某面包厂现年产值是15万元,计划今每年增加2万元,
(1)写出年产值Y(万元)与年数x之间的函数关系式;
(2)画出函数图象;
(3)求5年后的年产值.练习4．如图，已知A地在B地正南方3千米处，甲乙两人同时分别从A、B两地向正北方向匀速直行，他们与A地的距离S（千米）与所行的时间t（小时）之间的函数关系图象如图所示的AC和BD给出，当他们行走3小时后，他们之间的
距离为 千米.5.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) （C） （D）A1、某电视机厂要印刷产品宣传材料，甲印刷厂提出，每份材料收1元印刷费，另收1500元制版费，乙厂提出每份材料收2.5元印刷费，不收制版费。
（1）分别写出两厂收费y（元）与印制数量x（份）之间的关系式；
（2）在同一直角坐标系内作出它们的图象。
（3）根据图象回答下列问题。
印制800份宣传材料时，选择哪家印刷厂比较合算？
电视机厂拟拿出3000元用于印刷材料，找哪家印刷厂印制宣传材料能多一些？2、某单位急需用车，但又不准备买车，他们准备和一个体车主或一国营出租车公司其中一家签订月租车合同，设汽车每月行驶x千米，应付给个体车主的月费用 y1元，应付给出租公司的月租费是 y2元，、分别与x之间的函数关系图象如上图所示，观察图象回答下列问题。
（1）每月行驶的路程在什么范围内时，租国营公司的车合算？
（2）每月行驶的路程等于多少时，租两家的费用相同？
（3）如果这个单位估计每月行驶的路程为2300千米，那么这个单位租哪一家的车合算？二、A市和B市分别有某种库存机器12台和6台，现决定支援C村10台，D村8台，已知从A市调运一台机器到C村和D村的运费分别是400元和800元，B市调运一台机器到C村和D村的运费分别是300元和500元
（1）设B市运往C村机器x台，求总运费W（元）关于x的函数关系式，
（2）若要求总运费不超过9000元共有几种调运方案，
（3）求出总运费最低的调运方案，最低运费是多少？三、甲、乙两个仓库要向A、B两地运送水泥，已知甲库可调出100吨水泥，乙库可调出80吨水泥，A地需70吨水泥，B地需110吨水泥，两库到A、B两地的路程和运费如下表（表中运费栏“元/吨·千米”表示每吨水泥运送1千米所需人民币）：
（1）设甲库运往A地水泥x吨，求总运费y（元）关于x(吨)的函数关系式，
（2）当甲乙两库各运往A、B两地多少吨水泥时，总运费最省？最省的总运费是多少 ？