第一轮/第三章函数/3.3一次函数[下学期]
文档属性
| 名称 | 第一轮/第三章函数/3.3一次函数[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 115.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-11 14:20:00 | ||
图片预览




文档简介
课件11张PPT。一次函数(复习)温故而知新1.正比例函数的定义、图象、性质
y=kx(k≠0)是 函数,其图象是经过两点(0, )
和(1, )的一条直线.
(1)当k?0时,y随x的增大而 ,图象经过第 象限.
(2)当k?0时,y随x的增大而 ,图象经过第 象限.
2、一次函数的定义、图象、性质
y=kx+b(k≠0)是 函数,其图象是过(0, )的一条直线.
(1)当k?0时,y随x的增大而 .当k?0,且b?0时,图象经过第
象限;当k?0且b?0时,图象经过第 象限;
(2)当k?0时,y随x的增大而 .当k?0且b?0时,图象经过
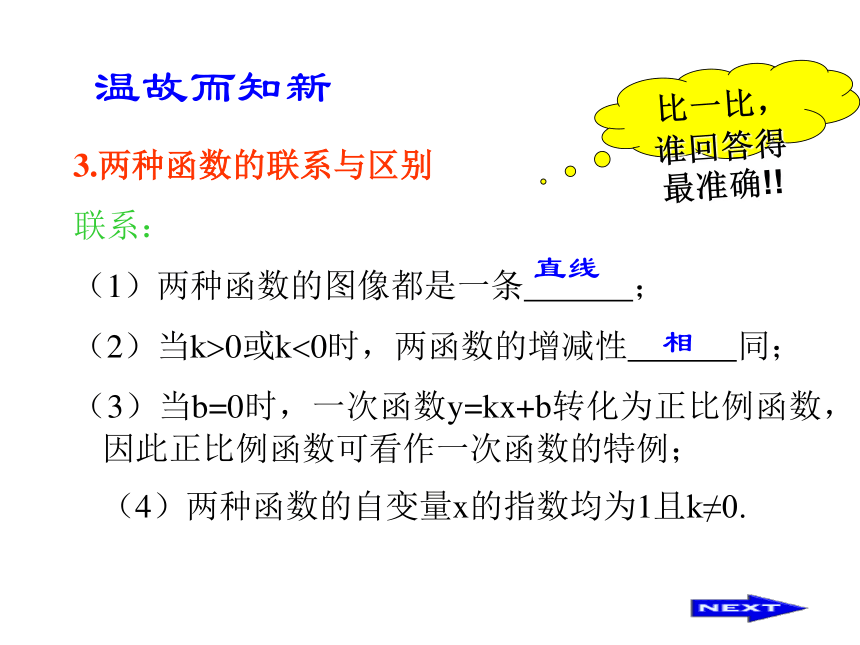
第 限,当k?0且b?0时,图象经过第 象限,正比例0K增大一、三减小二、四一次b增大一、二、三一、三、四减小一、二、四二、三、四 比一比,谁回答得最准确!!温故而知新3.两种函数的联系与区别
联系:
(1)两种函数的图像都是一条 ;
(2)当k?0或k?0时,两函数的增减性 同;
(3)当b=0时,一次函数y=kx+b转化为正比例函数,
直线相 比一比,谁回答得最准确!!因此正比例函数可看作一次函数的特例;(4)两种函数的自变量x的指数均为1且k≠0.区别:1)正比例函数也是 函数,但是一次函数 是正比例函数;2)正比例函数的图象一定经过 点,且经过 个象限,一般不经过 点, 且经过 个象限
一次原原两三不一定一次函数的图象
温故而知新4.求两种函数的解析式的方法是 .
待定系数法5、先设出式子中的未知系数,再根据条件求出未知系数,从而写出这个式的方法,叫做待定系数法.y=kx+b(k≠0,k,b为常数)这是一次函数的一般形式,当给定某些条件后则可用待定系数法求出k,b的值,以写出所要求的具体函数解析式.
6、如果直线y=k1x+b1和y=k2x+b2平行,则k1 k2.
= 哇!!同学们好厉害哦!!例1、已知y是x的一次函数,当x=-1时,y=2;当x=2时,y=-1,
求: (1)这个一次函数的关系式;
(2)当y=10时,x的值;
解:(1)由题意,设所求的一次函数的解析式是y=kx+b∵当x=-1时,y=2;当x=2时,y=-1,∴解这个方程组,得 ∴这个一次函数解析式是 y=-x+1(2) 当y=10时∴10=-x+1解得 x=-9例 2 已知一次函数y=(1-2m)x + (3m-1)
(1)当m取何值时,y随x的增大而减小?
(2)当m取何值时,函数的图像过原点?
(3)是否存在这样的整数m,使函数的图像经过第一、二、三象限?如果存在,请求出m的值;如果不存在,请说明理由解:(1) ∵函数y随x 的增大而减小∴1-2m<0即m>∴当m> 时,y随x的增大而减小(2)把x=0,y=0代入y=(1-2m)x + (3m-1)得3m-1=0,解得m=∴当m= 时,函数图像过原点(3)假设存在满足条件的m,依题意则有解得∴ < m< ,而m在这个范围内无整数解, ∴不存在这样的整数m(2005福州)百舸竞渡,激情飞扬。端午节期间,
某地举行龙舟比赛。甲、乙两支龙舟队在比赛时
路程y(米)与时间x(分钟)之间的函数图象
如图所示。根据图象回答下列问题:(1)1.8分钟时,哪支龙舟队处于领先位置?(2)在这次龙舟赛中,哪支龙舟队
先到达终点?先到达多少时间?(3)求乙队加速后,
路程y(米)与时间x(分钟)
之间的函数关系式 甲乙如图,正比例函数与一次函数的图像相交于
点A(3,4)且OA=OB,求:
(1)两个函数的关系式;
(2)A(3,4)CBxy220435(0,-5)归纳与整理1、理解一次函数与正比例函数的联系与区别2、熟练应用待定系数法求函数的解析式3、掌握一次函数的性质及学会其使用理一理练一练已知一次函数y=(1-2m)x+m-1,当m为何值时,函数y随着x的增大而减小,并且函数的图像经过第二、三、四象限?解: ∵函数y随着x的增大而减小,并且函数的图像经过第二、
三、四象限
∴解得:∴ < m < 1
y=kx(k≠0)是 函数,其图象是经过两点(0, )
和(1, )的一条直线.
(1)当k?0时,y随x的增大而 ,图象经过第 象限.
(2)当k?0时,y随x的增大而 ,图象经过第 象限.
2、一次函数的定义、图象、性质
y=kx+b(k≠0)是 函数,其图象是过(0, )的一条直线.
(1)当k?0时,y随x的增大而 .当k?0,且b?0时,图象经过第
象限;当k?0且b?0时,图象经过第 象限;
(2)当k?0时,y随x的增大而 .当k?0且b?0时,图象经过
第 限,当k?0且b?0时,图象经过第 象限,正比例0K增大一、三减小二、四一次b增大一、二、三一、三、四减小一、二、四二、三、四 比一比,谁回答得最准确!!温故而知新3.两种函数的联系与区别
联系:
(1)两种函数的图像都是一条 ;
(2)当k?0或k?0时,两函数的增减性 同;
(3)当b=0时,一次函数y=kx+b转化为正比例函数,
直线相 比一比,谁回答得最准确!!因此正比例函数可看作一次函数的特例;(4)两种函数的自变量x的指数均为1且k≠0.区别:1)正比例函数也是 函数,但是一次函数 是正比例函数;2)正比例函数的图象一定经过 点,且经过 个象限,一般不经过 点, 且经过 个象限
一次原原两三不一定一次函数的图象
温故而知新4.求两种函数的解析式的方法是 .
待定系数法5、先设出式子中的未知系数,再根据条件求出未知系数,从而写出这个式的方法,叫做待定系数法.y=kx+b(k≠0,k,b为常数)这是一次函数的一般形式,当给定某些条件后则可用待定系数法求出k,b的值,以写出所要求的具体函数解析式.
6、如果直线y=k1x+b1和y=k2x+b2平行,则k1 k2.
= 哇!!同学们好厉害哦!!例1、已知y是x的一次函数,当x=-1时,y=2;当x=2时,y=-1,
求: (1)这个一次函数的关系式;
(2)当y=10时,x的值;
解:(1)由题意,设所求的一次函数的解析式是y=kx+b∵当x=-1时,y=2;当x=2时,y=-1,∴解这个方程组,得 ∴这个一次函数解析式是 y=-x+1(2) 当y=10时∴10=-x+1解得 x=-9例 2 已知一次函数y=(1-2m)x + (3m-1)
(1)当m取何值时,y随x的增大而减小?
(2)当m取何值时,函数的图像过原点?
(3)是否存在这样的整数m,使函数的图像经过第一、二、三象限?如果存在,请求出m的值;如果不存在,请说明理由解:(1) ∵函数y随x 的增大而减小∴1-2m<0即m>∴当m> 时,y随x的增大而减小(2)把x=0,y=0代入y=(1-2m)x + (3m-1)得3m-1=0,解得m=∴当m= 时,函数图像过原点(3)假设存在满足条件的m,依题意则有解得∴ < m< ,而m在这个范围内无整数解, ∴不存在这样的整数m(2005福州)百舸竞渡,激情飞扬。端午节期间,
某地举行龙舟比赛。甲、乙两支龙舟队在比赛时
路程y(米)与时间x(分钟)之间的函数图象
如图所示。根据图象回答下列问题:(1)1.8分钟时,哪支龙舟队处于领先位置?(2)在这次龙舟赛中,哪支龙舟队
先到达终点?先到达多少时间?(3)求乙队加速后,
路程y(米)与时间x(分钟)
之间的函数关系式 甲乙如图,正比例函数与一次函数的图像相交于
点A(3,4)且OA=OB,求:
(1)两个函数的关系式;
(2)A(3,4)CBxy220435(0,-5)归纳与整理1、理解一次函数与正比例函数的联系与区别2、熟练应用待定系数法求函数的解析式3、掌握一次函数的性质及学会其使用理一理练一练已知一次函数y=(1-2m)x+m-1,当m为何值时,函数y随着x的增大而减小,并且函数的图像经过第二、三、四象限?解: ∵函数y随着x的增大而减小,并且函数的图像经过第二、
三、四象限
∴解得:∴ < m < 1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
