一次函数复习[下学期]

课件31张PPT。课程标准及学习目标2006年中考复习第六讲 函数3．函数：有的放矢(课标要求) (1)探索具体问题中的数量关系和变化规律[参见例8]
(2)函数
①通过简单实例，了解常量、变量的意义。
②能结合实例，了解函数的概念和三种表示方法，能举出函数的实例。 ③能结合图象对简单实际问题中的函数关系进行分析。[参见例9]
④能确定简单的整式、分式和简单实际问题中的函数的自变量取值范围，并会求出函数值。
⑤能用适当的函数表示法刻画某些实际问题中变量之间的关系。[参见例10]
⑥结合对函数关系的分析，尝试对变量的变化规律进行初步预测。[参见例11] (3)一次函数
①结合具体情境体会一次函数的意义，根据已知条件确定一次函数表达式。
②会画一次函数的图象，根据一次函数的图象和解析表达式y＝kx十b(k≠0)探索并理解其性质(k＞0或k＜0时，图象的变化情况)。
③理解正比例函数。
④能根据一次函数的图象求二元一次方程组的近似解。
⑤能用一次函数解决实际问题。 (4)反比例函数
①结合具体情境体会反比例函数的意义，能根据已知条件确定反比例函数表达式。
②能画出反比例函数的图象，根据图象和解析表达式y＝k/x(k≠o)探索并理解其性质(k＞0或k＜0时，图象的变化)。
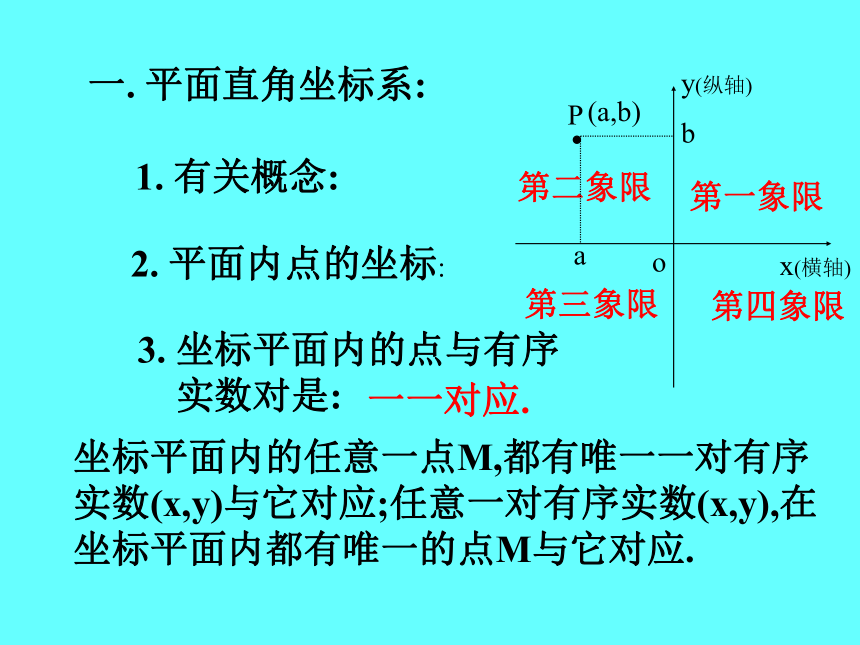
③能用反比例函数解决某些实际问题。 一. 平面直角坐标系:
1. 有关概念:x(横轴)y(纵轴)o第一象限第二象限第三象限第四象限Pab(a,b)2. 平面内点的坐标:3. 坐标平面内的点与有序
实数对是:一一对应.坐标平面内的任意一点M,都有唯一一对有序
实数(x,y)与它对应;任意一对有序实数(x,y),在
坐标平面内都有唯一的点M与它对应.4. 点的位置及其坐标特征:
①.各象限内的点:
②.各坐标轴上的点:
③.各象限角平分线上的点:
④.对称于坐标轴的两点:
⑤.对称于原点的两点:xyo(+,+)(-,+)(-,-)(+,-)P(a,0)Q(0,b)P(a,a)Q(b,-b)M(a,b)N(a,-b)A(x,y) B(-x,y)C(m,n)D(-m,-n)二、常量与变量
1.常量与变量：
在某一变化过程中，不断变化的数量叫变量.在某一变化过程中保持不变的量叫常量.
2.变量之间的关系:
在某一变化中,如果一个变量 Y随着另一个变量 X的变化而不断变化,那么X叫自变量,Y叫因变量.
知识点总结三、函数
1.一般地.在某个变化中,有两个变量x和y,如果给定一个x的值,相应地就确定了y的一个值,那么我们称y是x的函数,其中x叫自变量,y叫因变量.
2.要点：
①是一个变化的过程；
②有两个变量；
③这里的函数是一个单值函数;
④
⑤函数的实质是两个变量之间的关系.四、函数表示方法
解析法:用一个式子表示函数关系;
列表法:用列表的方法表示函数关系;
图象法:用图象的方法表示函数关系.变量间关系简捷明了,便于分析计算.需要通过计算,才能得到所需结果.能直接得到某些具体的对应值不能反映函数整体的变化情况直观表示了变量间变化过程和变化趋势.函数值只能是近似值..表达式是基础,是重点,表格是画图象的关键,图象是在表达式和表格的基础上对函数的总体概括和形象化的表达.五、一次函数
1.若两个变量x,y的关系可以表示成y=kx+b(k,b是常数,k≠0)的形式,则称y是做x的一次函数 (x为自变量,y为因变量).
2.特别地,当常数b＝0时,一次函数y=kx+b(k≠0)就成为:y=kx(k是常数,k≠0),称y是x的正比例函数.
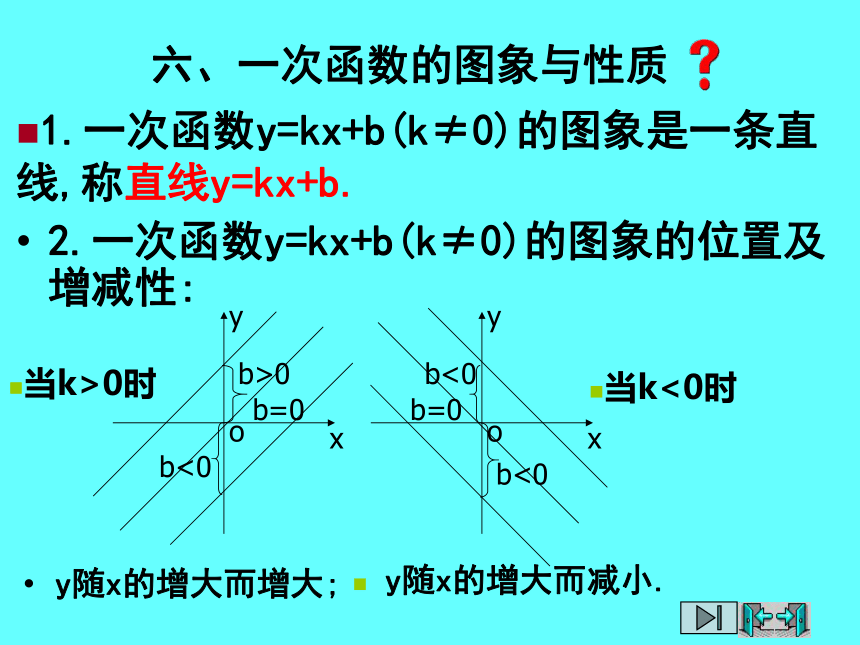
3.一次函数与正比例函数之间的关系:正比例函数是当b=0时的特殊的一次函数. 六、一次函数的图象与性质2.一次函数y=kx+b(k≠0)的图象的位置及增减性:y随x的增大而增大;1.一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.y随x的增大而减小.当k>0时当k<0时七、一次函数,一元一次方程,一元一次不等式(1)当y=0时,为一元一次方程kx+b=0,这时方程的解为:(2)当y>0时,为一元一次不等式kx+b>0;当y<0时,为一元一次不等式kx+b<0.这时不等式的解集分别为:一次函数,一元一次方程,一元一次不等式的关系Y=0 ·八、反比例函数2.要点:(1)自变量x≠0;
(2)比例系数k=xy;1.反比例函数的定义九、反比例函数的图象及性质1.形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;2.位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;九、反比例函数的图象及性质3.增减性 反比例函数的图象,当k>0时,在每一象限内,y随x的增大而减小;当k<0时,在每一象限内,y随x的增大而增大.4.图象的发展趋势 反比例函数的图象无限接近于x,y轴,但永远达不到x,y轴,画图象时,要体现出这个特点.
5.对称性 反比例函数的图象是关于原点成中心对称的图形.位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 y随x的增大而减小二四象限二四象限 y随x的增大而减小 y随x的增大而增大
填表分析正比例函数和反比例函数的区别十、正比例与反比例函数的联系与区别一. 选择题:
1如果A(2,m)与B(-2,-5)关于原点对称，则m=( )
A.-5 B. 1/5 C.5 D.
2.点P(a, b)满足 |a|+ b = 0,则点 P ( )
A.在x轴或y轴上 B.是坐标原点 C.在x轴上 D.在y轴上
3.下列命题中正确的是（ ）
A.点M(a,o)在第一或第四象
B.在坐标轴上的点的横, 纵坐标都是零
C.若点N(a,b)满足ab<0,则点N在第二,四象限
D.点P( 2,-3)到y轴的距离为3
4.下列函数中,关于x的正比例函数是 （ ）
A.y= -3x+1 B. y= x
C.y= -2x D. y= - x
5.函数 y = 的自变量取值范围是（ ）
A.x≤ 4 B.x≠±2
C.x≥2 D.x≤4且x≠±2-12CBCCD245减小>四> > xyo-5( 5 )解答题：
1.已知 ABC是等边三角形, 边长为2 , 求 ABC各顶点的坐标.
解：点A 的坐标是（0，0) ,
点B的坐标是（-2，0）
过C点作x轴的垂线 ,垂足为D,
D2.已知一次函数图象经过A(2,-1) 和点B，其中点B是另一条
直线y= 5x+3与y轴的交点，求这个一次函数的解析式.3. 如图，在同一坐标系中，关于x的一次函数
y = x+ b与 y = b x+1的图象只可能是（ ）C典型例题解析【例1】(1)(2003年·辽宁省)在平面直角坐标系中，点
P(-1，1)关于x轴的对称点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限(2)点P(3，-4)关于原点对称的点的坐标是 ( )
A.(3，-4) B.(-3，-4)
C.(3，4) D.(-3，4)(3)(2003年·黑龙江)平面直角坐标系内，点A(n,1-n)一定
不在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限CDC【例2】 求下列各函数的自变量x的取值范围.
(1)(2003年·昆明市)y= ；
(2)(2003年·贵阳市)y= ；
(3)(2003年·青海省)y= ；
(4)(2003年·河南省)y= .
典型例题解析x≠3x≥2x≥2且x≠32CA．甲是图①，乙是图②
B．甲是图③，乙是图②
C．甲是图①，乙是图④
D．甲是图③，乙是图④ 【例4】 (2003年，武汉市)小强在劳动技术课中要制作一个周长为80cm的等腰三角形，请你写出底边长ycm与一腰长xcm的函数关系式，并求出自变量x的取值范围.
解：y=80-2x
∵两边之和大于第三边且两边之差小于第三边
∴x-x＜y＜x+x∴0＜80-2x＜2x
即20＜x＜40
∴y=80-2x(20＜x＜40)典型例题解析【例5】 (1)在同一坐标系内，如图所示，直线
L1∶y=(k-2)x+k和L2∶y=kx的位置不可能为 ( )
典型例题解析A(2)如图所示，不可能是关于x的一次函数y=mx-(m-3)
的图像是 ( )
C【例6】 已知：如图所示，M(3，2)，N(1，-1).点P在
y轴上使PM+PN最短，求P点坐标.
P点坐标为(0，-1/4)解：如图，作M点关于y轴的对
称点M′(-3，2)，连接M′N，
交y轴于点P，则P点为所求，
设直线M′N解析式为y=kx+b，
则有：
故M′N∶y=- x- 令x=0得y=-
【例7】 (2003年·辽宁省)某博物馆每周都吸引大量中外游客前来参观.如果游客过多，对馆中的珍贵文物会产生不利影响.但同时考虑到文物的修缮和保存费用问题，还要保证一定的门票收入.因此，博物馆采取了涨浮门票价格的方法来控制参观人数.在该方法实施过程中发现：每周参观人数与票价之间存在着如图所示的一次函数关系.在这样的情况下，如果确保每周4万元的门票收入，那么每周应限定参观人数是多少?门票价格应是多少元?每周应限定参观人数为2000人，
门票价格为20元. 2.有效时间为33/5小时. 【例8】 (2003年·广西)在抗击“非典”过程中，某医药研究所开发了一种预防“非典”的药品.经试验这种药品的效果得知，当成人按规定剂量服用该药后1小时时，血液中含药量最高，达到每毫升5微克，接着逐步衰减，至8小时时血液中含药量为每毫升1.5微克，每毫升血液中含药量y(微克)随时间x(小时)的变化如图3-2-9所示.在成人按规定剂量服药后：
(1)分别求出x≤1，x≥1时，y与x之间的函数关系式.
(2)如果每毫升血液中含药量为2微克或2微克以上，对预防“非典”是有效的，那么这个有效时间为多少小时?
1. x≥1时，y=-1/2x+11/2