12.2三角形全等的判定 课时1 课件(共26张PPT)
文档属性
| 名称 | 12.2三角形全等的判定 课时1 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 08:47:09 | ||
图片预览






文档简介
(共26张PPT)
第1课时
12.2 三角形全等的判定
九年级上册 RJ
初中数学
1.什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
AB=DE, BC=EF, AC=DF,∠A=∠D, ∠B=∠E, ∠C=∠F.
2.已知△ABC≌△DEF,找出其中相等的边与相等的角.
A
B
C
E
D
F
知识回顾
1.理解并掌握三角形全等判定“边边边”条件的内容.
2.熟练利用“边边边”条件证明两个三角形全等.
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
学习目标
如果△ABC≌△A'B'C',则有对应边相等,对应角相等.
反之,根据全等三角形的定义,如果满足三条边分别相等,三个角分别相等,那么△ABC和△A'B'C'能够完全重合,即判定△ABC≌△A'B'C'.
课堂导入
是否必须同时满足三条边分别相等,三个角分别相等,才能保证两个三角形全等?如果只选取其中的一部分条件还能保证两个三角形全等吗?
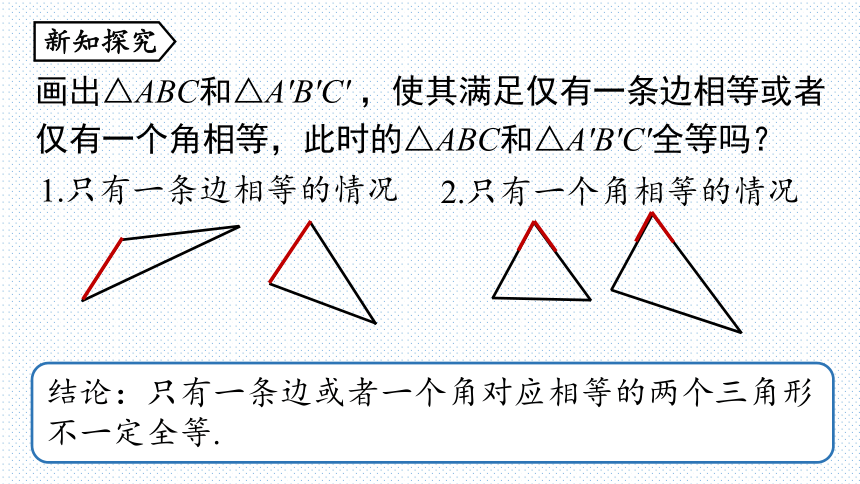
画出△ABC和△A'B'C' ,使其满足仅有一条边相等或者仅有一个角相等,此时的△ABC和△A'B'C'全等吗?
1.只有一条边相等的情况
2.只有一个角相等的情况
结论:只有一条边或者一个角对应相等的两个三角形不一定全等.
新知探究
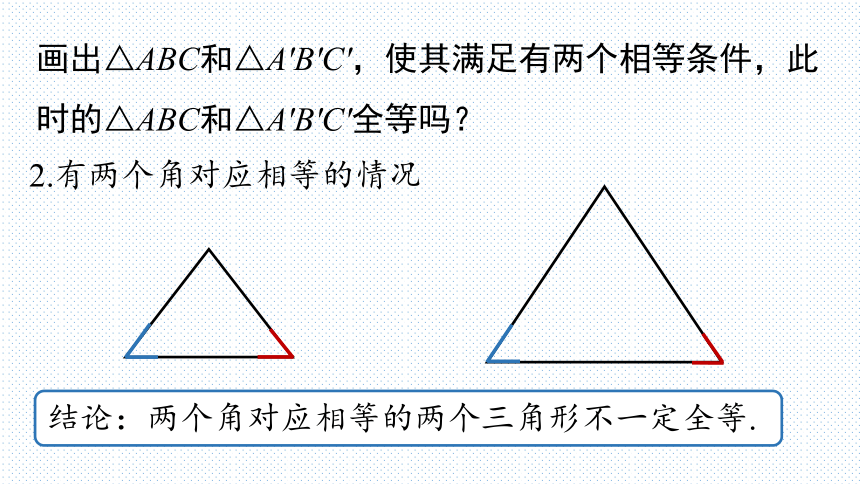
画出△ABC和△A'B'C',使其满足有两个相等条件,此时的△ABC和△A'B'C'全等吗?
1.有两条边对应相等的情况
结论:两条边对应相等的两个三角形不一定全等.
2.有两个角对应相等的情况
结论:两个角对应相等的两个三角形不一定全等.
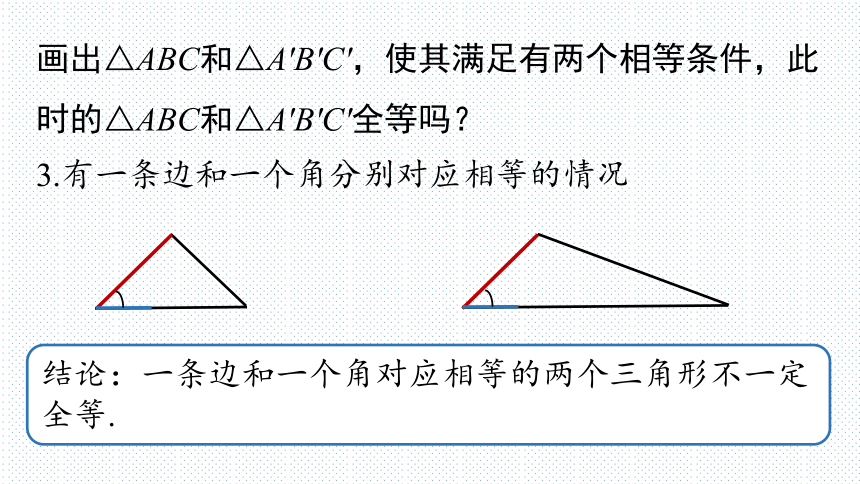
画出△ABC和△A'B'C',使其满足有两个相等条件,此时的△ABC和△A'B'C'全等吗?
3.有一条边和一个角分别对应相等的情况
结论:一条边和一个角对应相等的两个三角形不一定全等.
画出△ABC和△A'B'C',使其满足有两个相等条件,此时的△ABC和△A'B'C'全等吗?
1.有三条边对应相等的情况.
2.有两条边和一个角对应相等的情况.
3.有一条边和两个角对应相等的情况.
4.有三个角对应相等的情况.
画出△ABC和△A'B'C',使其满足有三个相等条件,此时的△ABC和△A'B'C'全等吗?
先画出一个△ABC,再画出一个△A'B'C',使得AB=A'B'
BC=B'C',CA=C'A',此时的△ABC和△A'B'C'全等吗?
作法:(1)画线段B'C' = BC;
(2)分别以B',C'为圆心,BA,
CA为半径画弧,两弧交点为A';
(3)连接线段A'B',A'C'.
1.有三条边对应相等的情况.
通过画图,你能得出什么样的结论?
B
C
A
B'
C'
A'
判定1:三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C'(SSS).
知识点1 三角形全等的基本事实:边边边(SSS)
新知探究
B
C
A
B'
C'
A'
例1 在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
证明:∵点D是BC的中点,∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴ △ABD≌△ACD (SSS).
A
B
C
D
跟踪训练
新知探究
AD称为公共边.
例2 如图,点C是AB的中点,AD=CE,CD=BE.求证△ACD≌△CBE.
证明:∵点C是AB的中点,∴AC=CB.
在△ACD和△CBE中,
AD=CE,
CD=BE,
AC=CB,
∴△ACD≌△CBE(SSS).
D
A
B
C
E
用直尺和圆规作出一个角等于已知角.
如图,已知:∠AOB.
求作:∠A'O'B',使得∠AOB=∠A'O'B'.
作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
知识点2 用直尺和圆规作一个角等于已知角
新知探究
(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
OC'=OC
(3)以点C'为圆心,CD长为半径画弧,与第(2)步中所画的弧相交于点D';
C'D'=CD
(4)过点D'画射线O'B',则∠AOB=∠A'O'B'.
O'D'=OD,三边相等
工人师傅常用角尺平分一个任意角.做法如下:
如图,∠AOB是一个任意角,在边OA,OB上分别截取OM=ON.移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?
证明:在△MOC和△NOC中,
∴△MOC≌△NOC(SSS).
∴∠MOC=∠NOC,则OC是∠AOB的平分线.
跟踪训练
新知探究
A
M
C
N
B
O
OM=ON,
OC=OC,
CM=CN,
解:△ABC≌△DCB. 理由:
在△ABC和△DCB中,
AB=CD
AC=BD
( )
∴△ ABC≌△DCB ( ).
1. 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.
BC=CB
B
D
A
C
随堂练习
SSS
2.如图,点D,F是线段BC上的两点,AB=CE,AF=DE,利用“SSS”判定,要使△ABF≌△ECD,还需要增加条件( ).
解:方法1 在△ABF和△ECD中,
AB=CE,
AF=ED,
BF=CD,
∴△ABF≌△ECD(SSS).
B
A
C
D
F
E
方法2 ∵BD=CF,∴BD+DF=CF+DF, 即BF=CD.
在△ABF和△ECD中,
AB=CE,
AF=ED,
BF=CD,
∴△ABF≌△ECD(SSS).
2.如图,点D,F是线段BC上的两点,AB=CE,AF=DE,利用“SSS”判定,要使△ABF≌△ECD,还需要增加条件( ).
BF=CD 或 BD=CF
B
A
C
D
F
E
证明:∵AD=FB,∴AD+DB=FB+BD,即AB=FD.
在△ABC和△FDE中,
AC=FE,
BC=DE,
AB=FD,
∴△ABC≌△FDE(SSS),
则∠A=∠F,∠ABC=∠FDE.
∴AC//EF,DE//BC.
3.已知:如图,AC=FE,AD=FB,BC=DE.求证:AC//EF,DE//BC.
A
C
B
D
E
F
4.如图,AB=AD,DC=BC,求证∠B=∠D.
解: 在△ABC和△ADC中,
AB=AD,
BC=DC,
AC=AC,
∴ △ABC≌△ADC(SSS).
∴∠B=∠D.
A
B
C
D
更多同类习题见《教材帮》数学RJ八上12.2节作业帮
三角形全等的判定
分类
探讨
SSS
尺规
作图
应用
只满足一个条件或者两个条件时不能判定三角形全等
三边分别相等的两个三角形全等
作一个角等于已知角
利用“SSS”解决实际问题
课堂小结
如图,AB=AC,DB=DC,请说明∠B=∠C.
解: 连接AD.
在△ABD和△ACD中,
AB=AC,
DB=DC,
AD=AD,
∴ △ABD≌△ACD(SSS).
∴∠B=∠C.
学会作辅助线帮助解题.
A
B
D
C
拓展提升
第1课时
12.2 三角形全等的判定
九年级上册 RJ
初中数学
1.什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
AB=DE, BC=EF, AC=DF,∠A=∠D, ∠B=∠E, ∠C=∠F.
2.已知△ABC≌△DEF,找出其中相等的边与相等的角.
A
B
C
E
D
F
知识回顾
1.理解并掌握三角形全等判定“边边边”条件的内容.
2.熟练利用“边边边”条件证明两个三角形全等.
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
学习目标
如果△ABC≌△A'B'C',则有对应边相等,对应角相等.
反之,根据全等三角形的定义,如果满足三条边分别相等,三个角分别相等,那么△ABC和△A'B'C'能够完全重合,即判定△ABC≌△A'B'C'.
课堂导入
是否必须同时满足三条边分别相等,三个角分别相等,才能保证两个三角形全等?如果只选取其中的一部分条件还能保证两个三角形全等吗?
画出△ABC和△A'B'C' ,使其满足仅有一条边相等或者仅有一个角相等,此时的△ABC和△A'B'C'全等吗?
1.只有一条边相等的情况
2.只有一个角相等的情况
结论:只有一条边或者一个角对应相等的两个三角形不一定全等.
新知探究
画出△ABC和△A'B'C',使其满足有两个相等条件,此时的△ABC和△A'B'C'全等吗?
1.有两条边对应相等的情况
结论:两条边对应相等的两个三角形不一定全等.
2.有两个角对应相等的情况
结论:两个角对应相等的两个三角形不一定全等.
画出△ABC和△A'B'C',使其满足有两个相等条件,此时的△ABC和△A'B'C'全等吗?
3.有一条边和一个角分别对应相等的情况
结论:一条边和一个角对应相等的两个三角形不一定全等.
画出△ABC和△A'B'C',使其满足有两个相等条件,此时的△ABC和△A'B'C'全等吗?
1.有三条边对应相等的情况.
2.有两条边和一个角对应相等的情况.
3.有一条边和两个角对应相等的情况.
4.有三个角对应相等的情况.
画出△ABC和△A'B'C',使其满足有三个相等条件,此时的△ABC和△A'B'C'全等吗?
先画出一个△ABC,再画出一个△A'B'C',使得AB=A'B'
BC=B'C',CA=C'A',此时的△ABC和△A'B'C'全等吗?
作法:(1)画线段B'C' = BC;
(2)分别以B',C'为圆心,BA,
CA为半径画弧,两弧交点为A';
(3)连接线段A'B',A'C'.
1.有三条边对应相等的情况.
通过画图,你能得出什么样的结论?
B
C
A
B'
C'
A'
判定1:三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C'(SSS).
知识点1 三角形全等的基本事实:边边边(SSS)
新知探究
B
C
A
B'
C'
A'
例1 在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
证明:∵点D是BC的中点,∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴ △ABD≌△ACD (SSS).
A
B
C
D
跟踪训练
新知探究
AD称为公共边.
例2 如图,点C是AB的中点,AD=CE,CD=BE.求证△ACD≌△CBE.
证明:∵点C是AB的中点,∴AC=CB.
在△ACD和△CBE中,
AD=CE,
CD=BE,
AC=CB,
∴△ACD≌△CBE(SSS).
D
A
B
C
E
用直尺和圆规作出一个角等于已知角.
如图,已知:∠AOB.
求作:∠A'O'B',使得∠AOB=∠A'O'B'.
作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
知识点2 用直尺和圆规作一个角等于已知角
新知探究
(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
OC'=OC
(3)以点C'为圆心,CD长为半径画弧,与第(2)步中所画的弧相交于点D';
C'D'=CD
(4)过点D'画射线O'B',则∠AOB=∠A'O'B'.
O'D'=OD,三边相等
工人师傅常用角尺平分一个任意角.做法如下:
如图,∠AOB是一个任意角,在边OA,OB上分别截取OM=ON.移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?
证明:在△MOC和△NOC中,
∴△MOC≌△NOC(SSS).
∴∠MOC=∠NOC,则OC是∠AOB的平分线.
跟踪训练
新知探究
A
M
C
N
B
O
OM=ON,
OC=OC,
CM=CN,
解:△ABC≌△DCB. 理由:
在△ABC和△DCB中,
AB=CD
AC=BD
( )
∴△ ABC≌△DCB ( ).
1. 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.
BC=CB
B
D
A
C
随堂练习
SSS
2.如图,点D,F是线段BC上的两点,AB=CE,AF=DE,利用“SSS”判定,要使△ABF≌△ECD,还需要增加条件( ).
解:方法1 在△ABF和△ECD中,
AB=CE,
AF=ED,
BF=CD,
∴△ABF≌△ECD(SSS).
B
A
C
D
F
E
方法2 ∵BD=CF,∴BD+DF=CF+DF, 即BF=CD.
在△ABF和△ECD中,
AB=CE,
AF=ED,
BF=CD,
∴△ABF≌△ECD(SSS).
2.如图,点D,F是线段BC上的两点,AB=CE,AF=DE,利用“SSS”判定,要使△ABF≌△ECD,还需要增加条件( ).
BF=CD 或 BD=CF
B
A
C
D
F
E
证明:∵AD=FB,∴AD+DB=FB+BD,即AB=FD.
在△ABC和△FDE中,
AC=FE,
BC=DE,
AB=FD,
∴△ABC≌△FDE(SSS),
则∠A=∠F,∠ABC=∠FDE.
∴AC//EF,DE//BC.
3.已知:如图,AC=FE,AD=FB,BC=DE.求证:AC//EF,DE//BC.
A
C
B
D
E
F
4.如图,AB=AD,DC=BC,求证∠B=∠D.
解: 在△ABC和△ADC中,
AB=AD,
BC=DC,
AC=AC,
∴ △ABC≌△ADC(SSS).
∴∠B=∠D.
A
B
C
D
更多同类习题见《教材帮》数学RJ八上12.2节作业帮
三角形全等的判定
分类
探讨
SSS
尺规
作图
应用
只满足一个条件或者两个条件时不能判定三角形全等
三边分别相等的两个三角形全等
作一个角等于已知角
利用“SSS”解决实际问题
课堂小结
如图,AB=AC,DB=DC,请说明∠B=∠C.
解: 连接AD.
在△ABD和△ACD中,
AB=AC,
DB=DC,
AD=AD,
∴ △ABD≌△ACD(SSS).
∴∠B=∠C.
学会作辅助线帮助解题.
A
B
D
C
拓展提升
