1.4.1 有理数的乘法 课件(共49张PPT)
文档属性
| 名称 | 1.4.1 有理数的乘法 课件(共49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 816.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 08:37:31 | ||
图片预览





文档简介
(共49张PPT)
1.4 有理数的乘除法
1.4.1 有理数的乘法
第一课时
第二课时
人教版 数学 七年级 上册
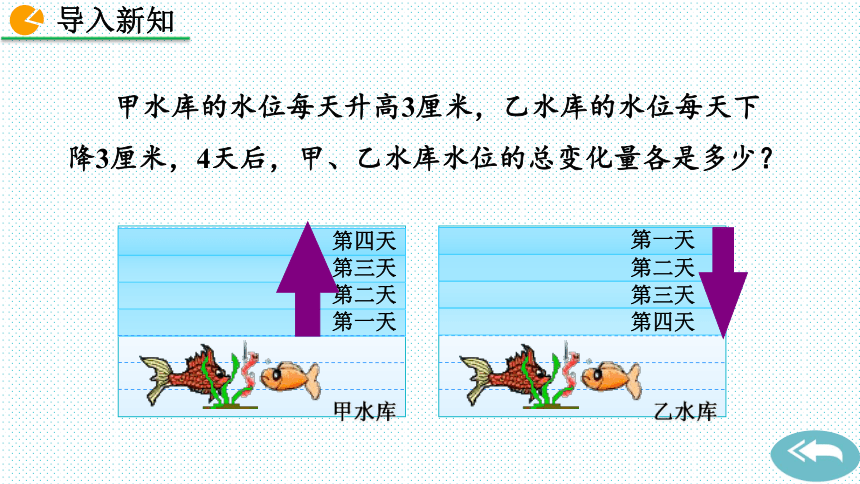
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后,甲、乙水库水位的总变化量各是多少?
甲水库
第一天
乙水库
第二天
第三天
第四天
第一天
第二天
第三天
第四天
导入新知
素养目标
1.经历有理数乘法的探索过程,掌握有理数的乘法法则并能进行熟练地运算.
2.掌握多个有理数相乘的积的符号法则.
3.理解有理数倒数的意义,会求一个有理数的倒数.
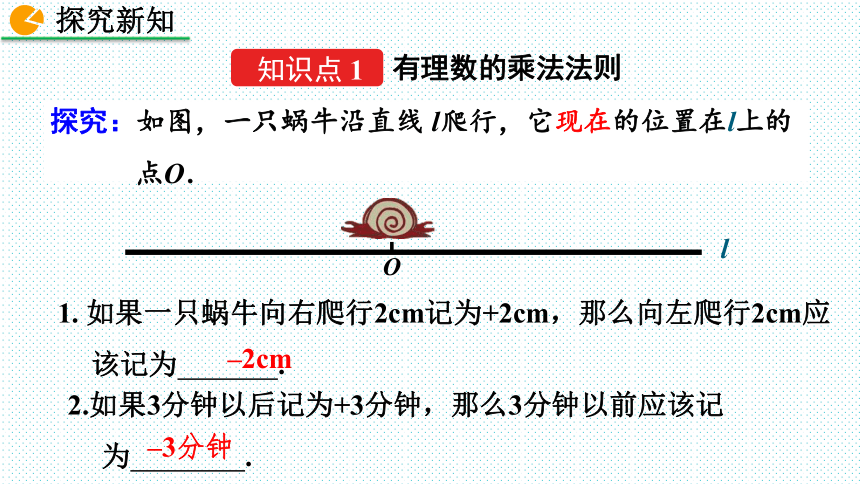
探究:如图,一只蜗牛沿直线 l爬行,它现在的位置在l上的点O.
l
O
1. 如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为 .
–2cm
–3分钟
有理数的乘法法则
知识点 1
探究新知
1.如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
2.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
3.如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
4.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
5.原地不动或运动了零次,结果是什么?
规定:向左为负,向右为正.
现在以前为负,现在以后为正.
为了区分方向与时间,
【思考】
探究新知
2
0
2
6
4
l
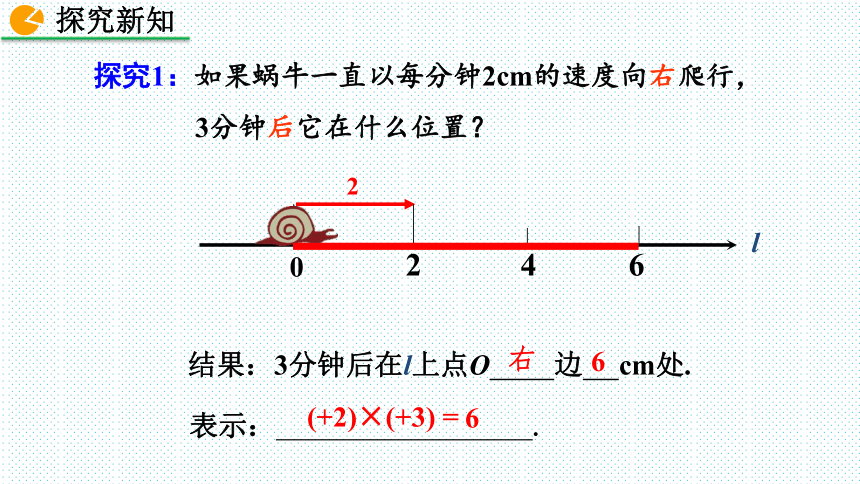
结果:3分钟后在l上点O 边 cm处.
表示: .
右
6
(+2)×(+3) =
探究1:如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
探究新知
6
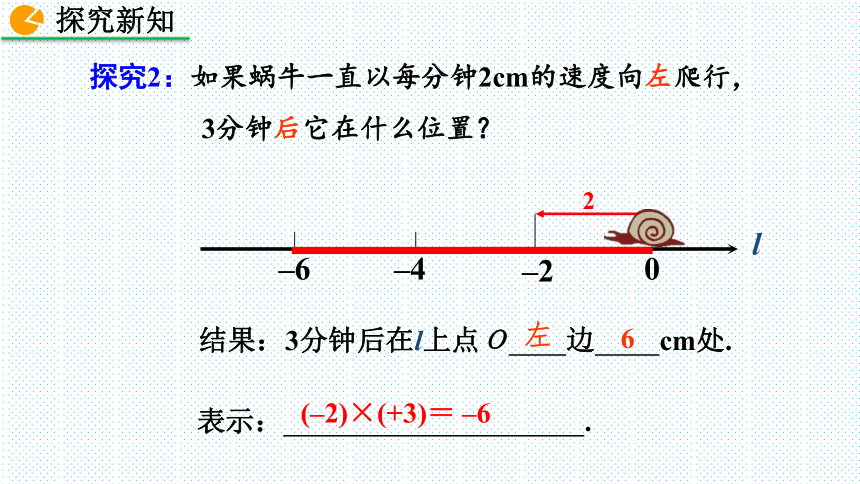
探究2:如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
–6
–4
0
–2
2
l
结果:3分钟后在l上点O 边 cm处.
左
6
表示: .
(–2)×(+3)=
探究新知
–6
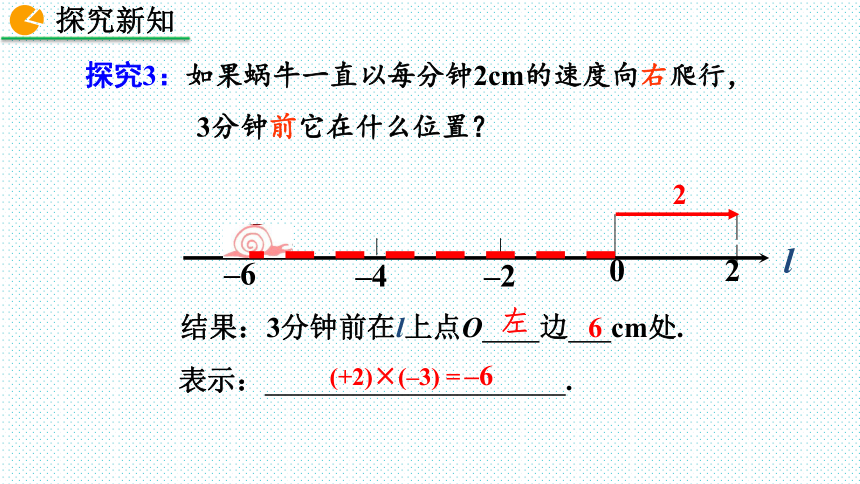
探究3:如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
2
–6
–4
0
–2
2
l
结果:3分钟前在l上点O 边 cm处.
表示: .
(+2)×(–3) =
–6
左
6
探究新知
探究 4:如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
2
0
2
6
4
–2
l
结果:3钟分前在l上点O 边 cm处.
右
6
表示: .
(–2)×(–3) =
+6
探究新知
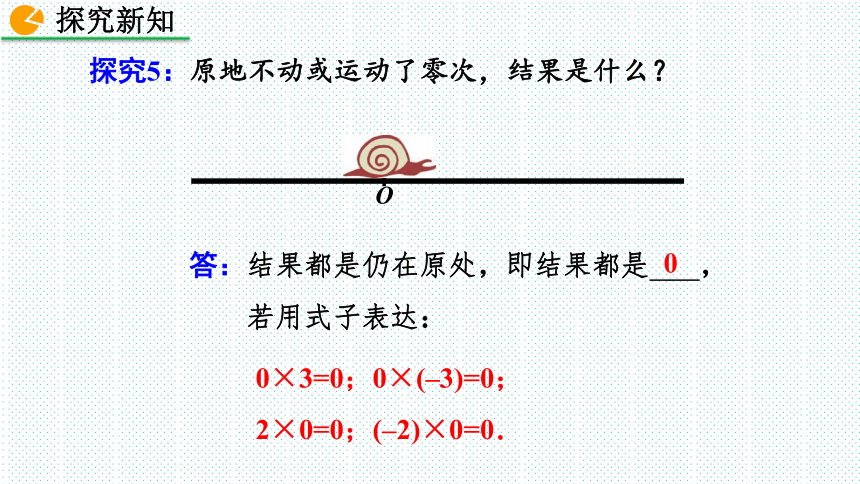
答:结果都是仍在原处,即结果都是 ,
若用式子表达:
探究5:原地不动或运动了零次,结果是什么?
0×3=0;0×(–3)=0;
2×0=0;(–2)×0=0.
0
O
探究新知
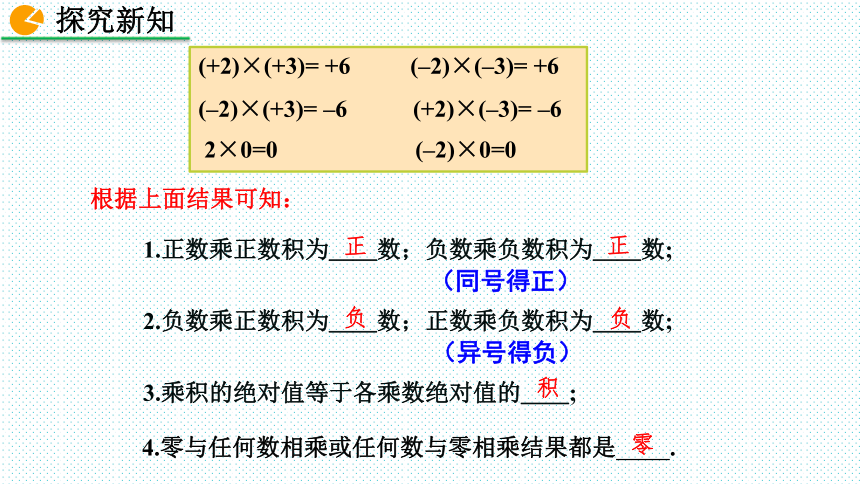
1.正数乘正数积为__数;负数乘负数积为__数;
2.负数乘正数积为__数;正数乘负数积为__数;
3.乘积的绝对值等于各乘数绝对值的__;
正
正
负
负
积
(同号得正)
(异号得负)
4.零与任何数相乘或任何数与零相乘结果都是 .
零
根据上面结果可知:
(+2)×(+3)= +6 (–2)×(–3)= +6
(–2)×(+3)= –6 (+2)×(–3)= –6
2×0=0 (–2)×0=0
探究新知
总结:有理数乘法法则
1. 两数相乘,同号得正,异号得负,并把绝对值相乘.
2. 任何数同0相乘,都得0.
讨论:
(1)若a<0, b>0, 则ab 0 ;
(2)若a<0, b<0, 则ab 0 ;
(3)若ab>0, 则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
探究新知
= (3×4) = +(3×4)
例1 计算:
(1)9×6 ; (2)( 9)×6 ;
(2)3 ×(–4); (4)(–3)×(–4).
解:(1)1 9×6 (2) ( 9)×6
= +(9×6) = (9×6)
= 54; = 54;
(3)3×(–4) (4)(–3)×(–4)
= 12;
有理数乘法的求解步骤:
先确定积的符号
再确定积的绝对值
= 12;
素养考点 1
两个数相乘的乘法法则的应用
探究新知
1.填写下表:
被乘数 乘数 积的符号 绝对值 结果
–5 7
15 6
–30 –6
4 –25
–
–
+
+
–35
+90
+180
–100
35
90
180
100
巩固练习
【议一议】下列各式的积是正的还是负的?
1. 2×3×4×(–5)
2. 2×3×(–4)×(–5)
3. 2×(–3)×(–4)×(–5)
4. (–2)×(–3)×(–4)×(–5)
5. 7.8×(–8.1)×0×(–19.6)
负
正
负
正
零
【思考】几个有理数相乘,因数都不为 0 时,积的符号怎样确定? 有一个因数为 0 时,积是多少?
知识点 2
多个数相乘的符号法则
探究新知
几个不等于零的数相乘,积的符号由_____________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
几个数相乘,如果其中有因数为0,_________.
负因数的个数
奇数
偶数
积等于0
}
奇负偶正
探究新知
归纳总结
例2 计算:
(1) (2)
解:(1)原式
(2)原式
素养考点 2
多个数相乘的符号法则的应用
探究新知
多个有理数相乘时若存在带分数,要先将其画成假分数,然后再进行计算.
2. 计算:
(1)( 4)×5×( 0.25); (2)
解:(1)( 4)×5 ×( 0.25)
= [ (4×5)]×( 0.25)
=+(20×0.25)
=5.
=( 20)×( 0.25)
解题后的反思:连续两次使用乘法法则,计算起来比较麻烦.
= 1 .
如果我们把乘法法则推广到三个以上有理数相乘,只“一次性地”先定号,再绝对值相乘即可.
巩固练习
(2)
【想一想】计算并观察结果有何特点?
(1) ×2; (2)(–0.25)×(–4)
倒数的概念:有理数中,乘积是1的两个数互为倒数.
【思考】数a(a≠0)的倒数是什么
(a≠0时,a的倒数是 )
倒数
知识点 3
探究新知
表示方法 符号 性质 特殊数0
倒数
相反数
互为倒数与互为相反数的区别
相同
积为1
没有倒数
a +(–a)=0
相异
和为0
相反数是自己
探究新知
求一个数的倒数的方法:
1. 求一个不为0的正数的倒数,就是将该整数作分母,1作分子;
2. 求一个真分数的倒数,就是将这个真分数的分母和分子交换位置;
3. 求一个带分数的倒数,先将该数化成假分数,再将其分子和分母的位置进行互换;
4. 求一个小数的倒数,先将该小数化为分数,再求其倒数 .
探究新知
3.说出下列各数的倒数.
1, –1, , , 5, –5, 0.75, .
1,
–1,
3,
–3,
巩固练习
.
2. 计算(–1)×(–2)的结果是( )
A.2 B.1 C.–2 D.–3
连接中考
1. 8的倒数是( )
A.–8 B.8 C.– D.
D
A
巩固练习
2. –2×(–5)的值是( )
A.–7 B.7 C.–10 D.10
基础巩固题
B
D
1. 2的倒数是( )
A.2 B. C.– D.–2
课堂检测
基础巩固题
3. 若a、b互为相反数,若x、y互为倒数,则a–xy+b= .
4. 相反数等于它本身的数是 ;倒数等于它本身的数是 ;绝对值等于它本身的数是 .
–1
0
1,–1
非负数
课堂检测
计算:
(2)
(3)
能力提升题
课堂检测
(1)
气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃. 已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少?
解:(–6)×9= – 54(℃);
21+(–54)= –33(℃).
答:甲地上空9km处的气温大约为–33℃.
拓广探索题
课堂检测
1. 有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2. 几个不是零的数相乘,负因数的个数为
奇数时,积为负数;
偶数时,积为正数.
课堂小结
问题:1.有理数的乘法法则是什么?
2.如何进行多个有理数的乘法运算?
3.小学时候大家学过乘法的哪些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和零相乘,都得0 .
乘法交换律、乘法结合律、乘法分配律.
(1)定号(奇负偶正);(2)算值(积的绝对值).
导入新知
素养目标
1.掌握乘法的分配律,并能灵活运用.
2.掌握有理数乘法的运算律,并利用运算律简化乘法运算.
第一组:
2. (3×4)×0.25= 3×(4×0.25)=
3. 2×(3+4)= 2×3+2×4=
1. 2×3= 3×2=
【思考】上面每小组运算分别体现了什么运算律?
2×3 3×2
(3×4)×0.25 3×(4×0.25)
2×(3+4) 2×3+2×4
6
6
3
3
14
14
=
=
=
有理数乘法的运算律
知识点 1
探究新知
5×(–4) =
15–35=
第二组:
2. [3×(–4)]×(– 5)=
3×[(–4)×(–5)]=
3. 5×[3+(–7 )]=
5×3+5×(–7 )=
1. 5×(–6) = (–6 )×5=
–30
–30
60
60
–20
–20
5× (–6) (–6) ×5
[3×(–4)]×(– 5) 3×[(–4)×(–5)]
5×[3+(–7 )] 5×3+5×(–7 )
=
=
=
(–12)×(–5) =
3×20=
探究新知
1.第一组式子中数的范围是 ________;
2.第二组式子中数的范围是 ________;
3.比较第一组和第二组中的算式,可以发现
________________________________.
正数
有理数
各运算律在有理数范围内仍然适用
探究新知
归纳总结
两个数相乘,交换两个因数的位置,积相等.
ab=ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
(ab)c = a(bc)
1.乘法交换律:
2.乘法结合律:
数的范围已扩展到有理数.
注意:用字母表示乘数时,“×”号可以写成“·”或省略,如a×b可以写成a·b或ab.
探究新知
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
3.乘法分配律:
a(b+c)
ab+ac
=
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.
探究新知
根据分配律可以推出:
一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
a(b+c+d )=ab+ac+ad
探究新知
例1 计算:(–85)×(–25)×(–4)
解:原式=(–85)×[(–25)×(–4)]
=(–85)×100
=–8500
素养考点 1
利用乘法运算律进行简便运算
探究新知
=[–8×(–0.125)] ×[(–12) ×(– )] ×(–0.1)
解:原式= –8×(–0.125) ×(–12) ×(– ) ×(–0.1)
1.计算: (–8)×(–12)×(–0.125)×(– )×(–0.1)
=1×4×(–0.1)
= –0.4
巩固练习
例2 用两种方法计算
解法1:
原式=
=
=–1
解法2:
原式=
=3+2–6
=–1
素养考点 2
利用乘法分配律进行简便运算
探究新知
解:(1)原式=
=
(2)原式=
=
= -22
(1)(– )×(8– –4)
(2)(–11)×(– )+(–11)×2 +(–11)×(– )
2.计算:
巩固练习
=
3.如何计算 71 ×(–9)?
提示:把 拆分成 .
解:原式=
=
=
=
巩固练习
1.已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A.a>0,b>0 B.a<0,b>0
C.a、b同号 D.a、b异号,且正数的绝对值较大
连接中考
分析:∵ab<0,∴a,b异号,
∵a+b>0,
∴正数的绝对值较大.
D
巩固练习
连接中考
利用运算律有时能进行简便运算.
例1 98×12=(100-2) ×12=1200-24=1176
例2 (-16) ×223+17×233=(-16+17) ×233=233
巩固练习
2.
请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(-15);
(2) .
分析:(1)将式子变形为(1000-1)×(-15),再根据乘法分配
律计算即可求解;
(2)根据乘法分配律计算即可求解.
连接中考
巩固练习
解:(1)999×(-15)
=(1000-1) ×(-15)
=1000×(-15)+15
= -15000+15
= -14985
(2)
=
=
= 99900
1.计算(–2)×(3– ),用乘法分配律计算过程正确的是( )
A. (–2)×3+(–2)×(– )
B. (–2)×3–(–2)×(– )
C. 2×3–(–2)×(– )
D.(–2)×3+2×(– )
A
基础巩固题
课堂检测
2.如果有三个数的积为正数,那么三个数中负数的个数是( )
A. 1 B. 0或2 C. 3 D. 1或3
3. 有理数a, b, c满足a+b+c>0,且abc<0,则在a, b, c中,正数的个数( )
A. 0 B. 1 C.2 D. 3
课堂检测
B
C
计算:
解:原式=
=
=
能力提升题
课堂检测
现定义两种运算:“ ”“ ”,对于任意两个整数a,b,a b=a+b–1,a b=a×b–1,计算:
(1)(6 8) (3 5);
(2)[4 (–2)] [(–5) (–3)].
解:原式=(6+8–1) (3×5–1)=13 14=13+14–1=26
解:原式=(–8–1) (–8–1)=(–9)×(–9)–1=80
拓广探索题
课堂检测
乘法
运算律
乘法
交换律
两个数相乘,交换两个因数的位置,积不变. ab=ba
乘法
结合律
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变. (ab)c = a(bc)
乘法
分配律
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
a(b+c)=ab+ac
课堂小结
1.4 有理数的乘除法
1.4.1 有理数的乘法
第一课时
第二课时
人教版 数学 七年级 上册
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后,甲、乙水库水位的总变化量各是多少?
甲水库
第一天
乙水库
第二天
第三天
第四天
第一天
第二天
第三天
第四天
导入新知
素养目标
1.经历有理数乘法的探索过程,掌握有理数的乘法法则并能进行熟练地运算.
2.掌握多个有理数相乘的积的符号法则.
3.理解有理数倒数的意义,会求一个有理数的倒数.
探究:如图,一只蜗牛沿直线 l爬行,它现在的位置在l上的点O.
l
O
1. 如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为 .
–2cm
–3分钟
有理数的乘法法则
知识点 1
探究新知
1.如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
2.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
3.如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
4.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
5.原地不动或运动了零次,结果是什么?
规定:向左为负,向右为正.
现在以前为负,现在以后为正.
为了区分方向与时间,
【思考】
探究新知
2
0
2
6
4
l
结果:3分钟后在l上点O 边 cm处.
表示: .
右
6
(+2)×(+3) =
探究1:如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
探究新知
6
探究2:如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
–6
–4
0
–2
2
l
结果:3分钟后在l上点O 边 cm处.
左
6
表示: .
(–2)×(+3)=
探究新知
–6
探究3:如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
2
–6
–4
0
–2
2
l
结果:3分钟前在l上点O 边 cm处.
表示: .
(+2)×(–3) =
–6
左
6
探究新知
探究 4:如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
2
0
2
6
4
–2
l
结果:3钟分前在l上点O 边 cm处.
右
6
表示: .
(–2)×(–3) =
+6
探究新知
答:结果都是仍在原处,即结果都是 ,
若用式子表达:
探究5:原地不动或运动了零次,结果是什么?
0×3=0;0×(–3)=0;
2×0=0;(–2)×0=0.
0
O
探究新知
1.正数乘正数积为__数;负数乘负数积为__数;
2.负数乘正数积为__数;正数乘负数积为__数;
3.乘积的绝对值等于各乘数绝对值的__;
正
正
负
负
积
(同号得正)
(异号得负)
4.零与任何数相乘或任何数与零相乘结果都是 .
零
根据上面结果可知:
(+2)×(+3)= +6 (–2)×(–3)= +6
(–2)×(+3)= –6 (+2)×(–3)= –6
2×0=0 (–2)×0=0
探究新知
总结:有理数乘法法则
1. 两数相乘,同号得正,异号得负,并把绝对值相乘.
2. 任何数同0相乘,都得0.
讨论:
(1)若a<0, b>0, 则ab 0 ;
(2)若a<0, b<0, 则ab 0 ;
(3)若ab>0, 则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
探究新知
= (3×4) = +(3×4)
例1 计算:
(1)9×6 ; (2)( 9)×6 ;
(2)3 ×(–4); (4)(–3)×(–4).
解:(1)1 9×6 (2) ( 9)×6
= +(9×6) = (9×6)
= 54; = 54;
(3)3×(–4) (4)(–3)×(–4)
= 12;
有理数乘法的求解步骤:
先确定积的符号
再确定积的绝对值
= 12;
素养考点 1
两个数相乘的乘法法则的应用
探究新知
1.填写下表:
被乘数 乘数 积的符号 绝对值 结果
–5 7
15 6
–30 –6
4 –25
–
–
+
+
–35
+90
+180
–100
35
90
180
100
巩固练习
【议一议】下列各式的积是正的还是负的?
1. 2×3×4×(–5)
2. 2×3×(–4)×(–5)
3. 2×(–3)×(–4)×(–5)
4. (–2)×(–3)×(–4)×(–5)
5. 7.8×(–8.1)×0×(–19.6)
负
正
负
正
零
【思考】几个有理数相乘,因数都不为 0 时,积的符号怎样确定? 有一个因数为 0 时,积是多少?
知识点 2
多个数相乘的符号法则
探究新知
几个不等于零的数相乘,积的符号由_____________决定.
当负因数有_____个时,积为负;
当负因数有_____个时,积为正.
几个数相乘,如果其中有因数为0,_________.
负因数的个数
奇数
偶数
积等于0
}
奇负偶正
探究新知
归纳总结
例2 计算:
(1) (2)
解:(1)原式
(2)原式
素养考点 2
多个数相乘的符号法则的应用
探究新知
多个有理数相乘时若存在带分数,要先将其画成假分数,然后再进行计算.
2. 计算:
(1)( 4)×5×( 0.25); (2)
解:(1)( 4)×5 ×( 0.25)
= [ (4×5)]×( 0.25)
=+(20×0.25)
=5.
=( 20)×( 0.25)
解题后的反思:连续两次使用乘法法则,计算起来比较麻烦.
= 1 .
如果我们把乘法法则推广到三个以上有理数相乘,只“一次性地”先定号,再绝对值相乘即可.
巩固练习
(2)
【想一想】计算并观察结果有何特点?
(1) ×2; (2)(–0.25)×(–4)
倒数的概念:有理数中,乘积是1的两个数互为倒数.
【思考】数a(a≠0)的倒数是什么
(a≠0时,a的倒数是 )
倒数
知识点 3
探究新知
表示方法 符号 性质 特殊数0
倒数
相反数
互为倒数与互为相反数的区别
相同
积为1
没有倒数
a +(–a)=0
相异
和为0
相反数是自己
探究新知
求一个数的倒数的方法:
1. 求一个不为0的正数的倒数,就是将该整数作分母,1作分子;
2. 求一个真分数的倒数,就是将这个真分数的分母和分子交换位置;
3. 求一个带分数的倒数,先将该数化成假分数,再将其分子和分母的位置进行互换;
4. 求一个小数的倒数,先将该小数化为分数,再求其倒数 .
探究新知
3.说出下列各数的倒数.
1, –1, , , 5, –5, 0.75, .
1,
–1,
3,
–3,
巩固练习
.
2. 计算(–1)×(–2)的结果是( )
A.2 B.1 C.–2 D.–3
连接中考
1. 8的倒数是( )
A.–8 B.8 C.– D.
D
A
巩固练习
2. –2×(–5)的值是( )
A.–7 B.7 C.–10 D.10
基础巩固题
B
D
1. 2的倒数是( )
A.2 B. C.– D.–2
课堂检测
基础巩固题
3. 若a、b互为相反数,若x、y互为倒数,则a–xy+b= .
4. 相反数等于它本身的数是 ;倒数等于它本身的数是 ;绝对值等于它本身的数是 .
–1
0
1,–1
非负数
课堂检测
计算:
(2)
(3)
能力提升题
课堂检测
(1)
气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃. 已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少?
解:(–6)×9= – 54(℃);
21+(–54)= –33(℃).
答:甲地上空9km处的气温大约为–33℃.
拓广探索题
课堂检测
1. 有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2. 几个不是零的数相乘,负因数的个数为
奇数时,积为负数;
偶数时,积为正数.
课堂小结
问题:1.有理数的乘法法则是什么?
2.如何进行多个有理数的乘法运算?
3.小学时候大家学过乘法的哪些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和零相乘,都得0 .
乘法交换律、乘法结合律、乘法分配律.
(1)定号(奇负偶正);(2)算值(积的绝对值).
导入新知
素养目标
1.掌握乘法的分配律,并能灵活运用.
2.掌握有理数乘法的运算律,并利用运算律简化乘法运算.
第一组:
2. (3×4)×0.25= 3×(4×0.25)=
3. 2×(3+4)= 2×3+2×4=
1. 2×3= 3×2=
【思考】上面每小组运算分别体现了什么运算律?
2×3 3×2
(3×4)×0.25 3×(4×0.25)
2×(3+4) 2×3+2×4
6
6
3
3
14
14
=
=
=
有理数乘法的运算律
知识点 1
探究新知
5×(–4) =
15–35=
第二组:
2. [3×(–4)]×(– 5)=
3×[(–4)×(–5)]=
3. 5×[3+(–7 )]=
5×3+5×(–7 )=
1. 5×(–6) = (–6 )×5=
–30
–30
60
60
–20
–20
5× (–6) (–6) ×5
[3×(–4)]×(– 5) 3×[(–4)×(–5)]
5×[3+(–7 )] 5×3+5×(–7 )
=
=
=
(–12)×(–5) =
3×20=
探究新知
1.第一组式子中数的范围是 ________;
2.第二组式子中数的范围是 ________;
3.比较第一组和第二组中的算式,可以发现
________________________________.
正数
有理数
各运算律在有理数范围内仍然适用
探究新知
归纳总结
两个数相乘,交换两个因数的位置,积相等.
ab=ba
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
(ab)c = a(bc)
1.乘法交换律:
2.乘法结合律:
数的范围已扩展到有理数.
注意:用字母表示乘数时,“×”号可以写成“·”或省略,如a×b可以写成a·b或ab.
探究新知
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
3.乘法分配律:
a(b+c)
ab+ac
=
根据乘法交换律和结合律可以推出:
三个以上有理数相乘,可以任意交换因数的位置,也可先把其中的几个数相乘.
探究新知
根据分配律可以推出:
一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.
a(b+c+d )=ab+ac+ad
探究新知
例1 计算:(–85)×(–25)×(–4)
解:原式=(–85)×[(–25)×(–4)]
=(–85)×100
=–8500
素养考点 1
利用乘法运算律进行简便运算
探究新知
=[–8×(–0.125)] ×[(–12) ×(– )] ×(–0.1)
解:原式= –8×(–0.125) ×(–12) ×(– ) ×(–0.1)
1.计算: (–8)×(–12)×(–0.125)×(– )×(–0.1)
=1×4×(–0.1)
= –0.4
巩固练习
例2 用两种方法计算
解法1:
原式=
=
=–1
解法2:
原式=
=3+2–6
=–1
素养考点 2
利用乘法分配律进行简便运算
探究新知
解:(1)原式=
=
(2)原式=
=
= -22
(1)(– )×(8– –4)
(2)(–11)×(– )+(–11)×2 +(–11)×(– )
2.计算:
巩固练习
=
3.如何计算 71 ×(–9)?
提示:把 拆分成 .
解:原式=
=
=
=
巩固练习
1.已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A.a>0,b>0 B.a<0,b>0
C.a、b同号 D.a、b异号,且正数的绝对值较大
连接中考
分析:∵ab<0,∴a,b异号,
∵a+b>0,
∴正数的绝对值较大.
D
巩固练习
连接中考
利用运算律有时能进行简便运算.
例1 98×12=(100-2) ×12=1200-24=1176
例2 (-16) ×223+17×233=(-16+17) ×233=233
巩固练习
2.
请你参考黑板中老师的讲解,用运算律简便计算:
(1)999×(-15);
(2) .
分析:(1)将式子变形为(1000-1)×(-15),再根据乘法分配
律计算即可求解;
(2)根据乘法分配律计算即可求解.
连接中考
巩固练习
解:(1)999×(-15)
=(1000-1) ×(-15)
=1000×(-15)+15
= -15000+15
= -14985
(2)
=
=
= 99900
1.计算(–2)×(3– ),用乘法分配律计算过程正确的是( )
A. (–2)×3+(–2)×(– )
B. (–2)×3–(–2)×(– )
C. 2×3–(–2)×(– )
D.(–2)×3+2×(– )
A
基础巩固题
课堂检测
2.如果有三个数的积为正数,那么三个数中负数的个数是( )
A. 1 B. 0或2 C. 3 D. 1或3
3. 有理数a, b, c满足a+b+c>0,且abc<0,则在a, b, c中,正数的个数( )
A. 0 B. 1 C.2 D. 3
课堂检测
B
C
计算:
解:原式=
=
=
能力提升题
课堂检测
现定义两种运算:“ ”“ ”,对于任意两个整数a,b,a b=a+b–1,a b=a×b–1,计算:
(1)(6 8) (3 5);
(2)[4 (–2)] [(–5) (–3)].
解:原式=(6+8–1) (3×5–1)=13 14=13+14–1=26
解:原式=(–8–1) (–8–1)=(–9)×(–9)–1=80
拓广探索题
课堂检测
乘法
运算律
乘法
交换律
两个数相乘,交换两个因数的位置,积不变. ab=ba
乘法
结合律
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变. (ab)c = a(bc)
乘法
分配律
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
a(b+c)=ab+ac
课堂小结
