1.4.2 有理数的除法 课件(共48张PPT)
文档属性
| 名称 | 1.4.2 有理数的除法 课件(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 08:36:50 | ||
图片预览










文档简介
(共48张PPT)
1.4 有理数的乘除法
1.4.2 有理数的除法
第一课时
第二课时
人教版 数学 七年级 上册
根据实验测定,高度每增加1km,气温大概下降6℃. 某登山运动员攀登某高峰的途中发回信息,报告他所在高度的温度是-15℃,当时地面气温为3℃. 请问你能确定登山运动员所在的位置高度吗
导入新知
素养目标
1.认识有理数的除法,经历除法的运算过程.
2. 理解除法法则,体验除法与乘法的转化关系.
3.掌握有理数的除法及乘除混合运算.
知识点 1
有理数的除法及分数化简
探究新知
【想一想】我们在前面学习有理数的减法时,是借助于逆运算把它转化为加法来进行的.大家知道除法的逆运算是乘法,那么有理数的除法运算是不是也可以借助于逆运算转化为乘法来进行呢?
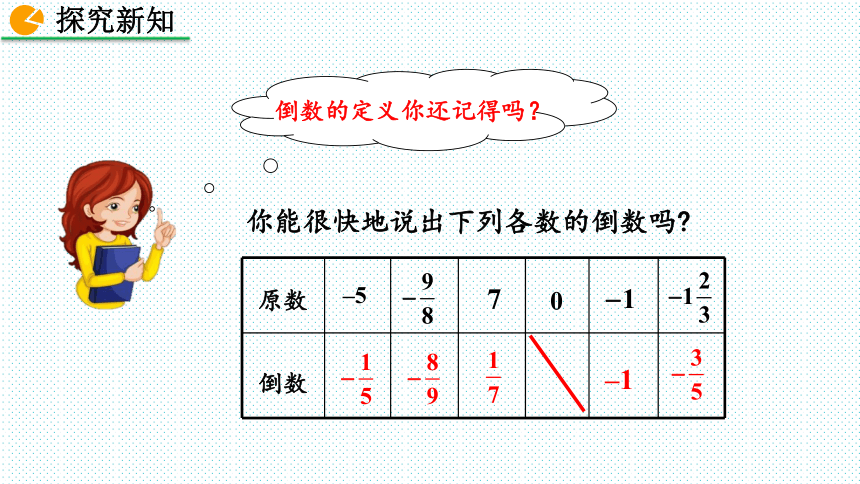
你能很快地说出下列各数的倒数吗
原数
倒数
–1
倒数的定义你还记得吗?
探究新知
–5
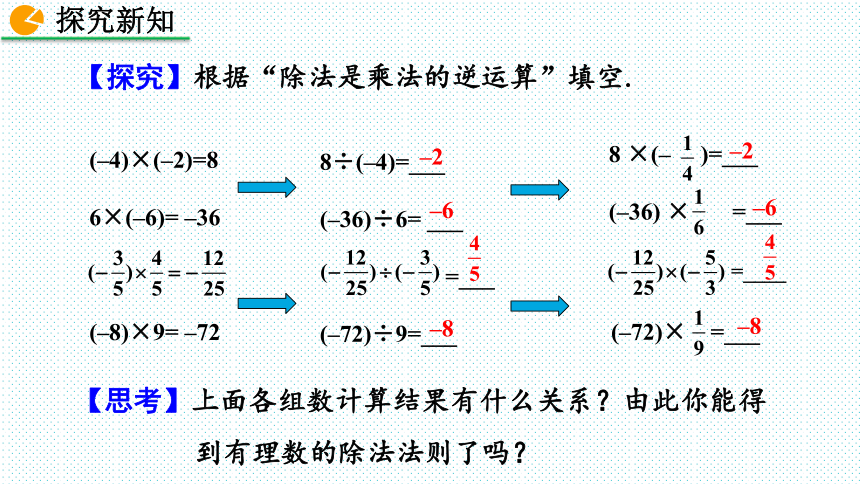
8÷(–4)=___
(–36)÷6= ___
=___
(–72)÷9=___
–2
–6
–8
(–4)×(–2)=8
6×(–6)= –36
(–8)×9= –72
【探究】根据“除法是乘法的逆运算”填空.
探究新知
8 ×(– )=___
(–36) × =___
(–72)× =___
–2
–6
–8
【思考】上面各组数计算结果有什么关系?由此你能得到有理数的除法法则了吗?
(1)(+6)÷(+2) =
+3
+3
(2)(+6)÷(–2) =
–3
–3
观察下列两组式子,你能找到它们的共同点吗?
“÷”变“×”
“÷”变“×”
互为倒数
互为倒数
从中你能得出什么结论?
探究新知
有理数除法法则(一)
用字母表示为
除以一个不等于0的数,等于乘这个数的倒数.
探究新知
利用上面的除法法则计算下列各题.
(1)(–54)÷ (–9); (2)(–27) ÷3;
(3)0 ÷ (–7); (4)(–24) ÷(–6).
【思考】从上面我们能发现商的符号有什么规律?
探究新知
6
–9
0
4
两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何一个不等于0的数,都得0.
有理数除法法则(二)
探究新知
到现在为止我们有了两个除法法则,那么两个法则是不是都可以用于解决两数相除呢?
1. 两个法则都可以用来求两个有理数相除.
2. 如果两数相除,能够整除的就选择法则二,不能够整除的就选择用法则一.
【思考】
探究新知
归纳总结
例1 计算(1)(–36) ÷ 9;
(2) .
解:(1)(–36) ÷ 9= –(36× )= –4;
(2)
素养考点 1
有理数除法的运算
探究新知
答案:(1)–4
(2)–8
(3)0
1.计算:
巩固练习
(4)
(1)24 ÷(-6)
(2)(-4) ÷
(3)0÷
(4)( ) ÷( )
例2 化简下列各式:
素养考点 2
有理数的化简
探究新知
(1) ;(2) .
解:(1)
(2)
2. 化简:
(1) = ÷ = .
(2) = = = .
(3) = _____.
–8
(–72)
9
(–30)÷(–45)
0
30÷45
巩固练习
例3 计算
(1) (2)
解:(1)原式=
=
=
=
=
有理数的乘除混合运算
知识点 2
探究新知
如果有带分数,可以将带分数写成整数部分和分数部分的和,利用分配律进行运算,更加简便.
(2)原式=
= 1
将小数化为分数
1. 有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
2. 乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算).
探究新知
归纳总结
(1)
(2)
解:原式=
=
=
解:原式=
=
=
=
3.计算
巩固练习
2. 计算:(–12) ÷ 3= .
连接中考
1. (–21) ÷7的结果是( )
A.3 B.–3 C. D. –
B
–4
巩固练习
1. 计算 2. 计算
基础巩固题
课堂检测
解:原式=
=
解:原式=
=
3. 计算
解:原式=
=
填空:
(1)若a,b互为相反数,且a ≠ b,则 =________;
(2)当a < 0时, =_______;
(3)若 ,则a,b的符号分别是__________.
(4)若–3x=12,则x =_____.
能力提升题
课堂检测
-4
若|2x+6|+|3–y|=0,则 = .
解析:由题意得,|2x+6|=0, |3–y|=0,
解得x = –3, y=3, 所以 = –1.
拓广探索题
课堂检测
–1
有理数的乘除运算
有理数除法法则
有理数乘除的转化
有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
乘除混合运算
乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算).
课堂小结
1.
2. 两数相除,同号得正,异号得负,并把绝对值相除. 0除以任何一个不等于0的数,都得0 .
数字入诗
明代南海才子伦文叙为苏东坡《百鸟归巢图》题的数学诗:
天生一只又一只,三四五六七八只。
凤凰何少鸟何多,啄尽人间千石谷!
诗中数字:一只又一只,
三四五六七八只。
请问何来百鸟呢
导入新知
在这些数中加上适当的运算符号就能得到100.
1+1+3×4+5×6+7×8=100
导入新知
诗中数字:一只又一只,
三四五六七八只。
1.掌握有理数加减乘除混合运算的顺序,能熟练地进行有理数加减乘除混合运算.
2.会用计算器进行有理数的加减乘除运算,会运用有理数的四则运算解决实际问题.
素养目标
问题1:小学的四则混合运算的顺序是怎样的?
先乘除,后加减,同级运算从左至右,有括号先算括号内,再算括号外. 括号计算顺序:先小括号,再中括号,最后大括号.
有理数的加减乘除混合运算
知识点 1
探究新知
问题2:我们目前都学习了哪些运算?
加法、减法、乘法、除法.
一个运算中,含有有理数的加、减、乘、除等多种运算,称为有理数的混合运算.
探究新知
探究1:下列式子含有哪几种运算?先算什么,后算什么?
加减运算
第一级运算
乘除运算
第二级运算
探究新知
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
有理数混合运算的顺序:
探究2:观察式子 ,应该按照什么顺序
来计算?
探究新知
归纳总结
(1)原式= 6–4=2
解:
(2)原式= –6 – 150= – 156
(3)原式= –28+3= –25
素养考点 1
有理数的混合运算
例1 计算:
(1)
(2)
(3)
探究新知
1.计算:
(1) ;(2) .
解析:先算括号里面的→除法转化为乘法→计算→结果.
巩固练习
解:(1)原式=
=
=
(2)原式=
=
=
=
例2 计算 .
按常规方法计算
解:方法一,
原式=
=
=
素养考点 2
有理数混合运算的简便计算
探究新知
= .
简便计算,先取倒数
方法二,
原式的倒数为
=
故
探究新知
=
=
解:原式的倒数为
故
2. 选择合适的方法计算:
巩固练习
例3 某公司去年1~3月平均每月亏损1.5万元,4~6月平均盈利2万元,7~10月平均盈利1.7万元,11~12月平均亏损2.3万元,这个公司去年总盈亏情况如何?
有理数混合运算的应用
素养考点 3
探究新知
解:记盈利额为正数,亏损额为负数,公司去年全年总的盈亏(单位:万元)为
(–1.5)×3+2×3+1.7×4+(–2.3)×2
= –4.5+6+6.8 –4.6
=3.7(万元)
答:这个公司去年全年盈利3.7万元.
3.一架直升飞机从高度为450m的位置开始,先以20m/s的速度上升60s,后以12m/s的速度下降120s,这时直升机所在的高度是多少?
解:450+20×60–12×120
=450+1200–1440
=210(m)
答:这时直升机所在的高度是210m.
巩固练习
利用计算器进行有理数的混合运算
知识点 2
1.计算器是一种方便实用的计算工具,用计算器进行比较复杂的数的计算比笔算要快捷得多.
2.提倡在明确算理的情况下,恰当地使用计算器进行一些比较复杂的有理数加减乘除法混合运算.
探究新知
【思考】如何用计数器进行有理数的混合运算 你会使用计算器计算
在用计算器进行有理数除法运算时,如果先确定商的符号,那么只需用计算器计算商的绝对值,可以减少按键的次数(对比有理数的乘法运算).
1
(–1.5)×3+2×3+1.7×4+(–2.3)×2吗?
(–)
如果计算器带符号键 ,
只需按键:
(–)
·
7
1
+
3
×
5
·
4
+
2
×
(–)
·
3
×
2
2
×
3
+
探究新知
1.某地某天的最高气温是6℃,最低气温是–4℃,则该地当天的温差为 ℃.
连接中考
2.计算的结果是( )
A.0 B.1 C.–1 D.
A
10
巩固练习
1.下列各式中,结果相等的是( )
A. 6÷(3×2)和 6÷3×2
B. (–120+400)÷20和–120+400÷20
C. –3–(4–7)和–3–4–7
D. –4×(2÷8)和 –4×2÷8
基础巩固题
课堂检测
D
(1)23×(–5)–(–3)÷
(2)–7×(–3)×(–0.5)+(–12)×(–2.6)
20.7
2.计算:
课堂检测
13
基础巩固题
(1)2×(–3÷)–4×(–3)+15;
(2)–8+(–3)×[–4÷(– )+2]–32÷(–2).
解:(1)原式=2×(–27)–(–12)+15
= –54+12+15
= –27
= –8+(–3)×18 –(–4.5)
(2)原式= –8+(–3)×(16+2)–9÷(–2)
= –8 –54+4.5
= –57.5
课堂检测
3.计算:
基础巩固题
解:原式=
阅读下面的解题过程:
计算
=(–15)÷(–25)
=
回答:(1)上面解题过程中有两处错误,
第一处错误是第 步,错误原因是_____________;
第二处错误是第 步,错误原因是_____________ .
(第一步)
(第二步)
(第三步)
二
运算顺序有误
三
结果有误
能力提升题
课堂检测
(2)写正确的解题过程.
解:
课堂检测
一天,小红与小莉利用温差测量山峰的高度,小红在山顶测得温度是–1℃,小莉此时在山脚测得温度是5℃. 已知该地区高度每增加100米,气温大约降低0.8℃,这个山峰的高度为多少 (山脚海拔0米)
拓广探索题
课堂检测
=6÷0.8×100
=750(米)
答: 这个山峰的高度为750米.
[5–(–1)]÷0.8×100
解:依题意得
课堂检测
有理数的加减乘除混合运算顺序
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
课堂小结
1.4 有理数的乘除法
1.4.2 有理数的除法
第一课时
第二课时
人教版 数学 七年级 上册
根据实验测定,高度每增加1km,气温大概下降6℃. 某登山运动员攀登某高峰的途中发回信息,报告他所在高度的温度是-15℃,当时地面气温为3℃. 请问你能确定登山运动员所在的位置高度吗
导入新知
素养目标
1.认识有理数的除法,经历除法的运算过程.
2. 理解除法法则,体验除法与乘法的转化关系.
3.掌握有理数的除法及乘除混合运算.
知识点 1
有理数的除法及分数化简
探究新知
【想一想】我们在前面学习有理数的减法时,是借助于逆运算把它转化为加法来进行的.大家知道除法的逆运算是乘法,那么有理数的除法运算是不是也可以借助于逆运算转化为乘法来进行呢?
你能很快地说出下列各数的倒数吗
原数
倒数
–1
倒数的定义你还记得吗?
探究新知
–5
8÷(–4)=___
(–36)÷6= ___
=___
(–72)÷9=___
–2
–6
–8
(–4)×(–2)=8
6×(–6)= –36
(–8)×9= –72
【探究】根据“除法是乘法的逆运算”填空.
探究新知
8 ×(– )=___
(–36) × =___
(–72)× =___
–2
–6
–8
【思考】上面各组数计算结果有什么关系?由此你能得到有理数的除法法则了吗?
(1)(+6)÷(+2) =
+3
+3
(2)(+6)÷(–2) =
–3
–3
观察下列两组式子,你能找到它们的共同点吗?
“÷”变“×”
“÷”变“×”
互为倒数
互为倒数
从中你能得出什么结论?
探究新知
有理数除法法则(一)
用字母表示为
除以一个不等于0的数,等于乘这个数的倒数.
探究新知
利用上面的除法法则计算下列各题.
(1)(–54)÷ (–9); (2)(–27) ÷3;
(3)0 ÷ (–7); (4)(–24) ÷(–6).
【思考】从上面我们能发现商的符号有什么规律?
探究新知
6
–9
0
4
两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何一个不等于0的数,都得0.
有理数除法法则(二)
探究新知
到现在为止我们有了两个除法法则,那么两个法则是不是都可以用于解决两数相除呢?
1. 两个法则都可以用来求两个有理数相除.
2. 如果两数相除,能够整除的就选择法则二,不能够整除的就选择用法则一.
【思考】
探究新知
归纳总结
例1 计算(1)(–36) ÷ 9;
(2) .
解:(1)(–36) ÷ 9= –(36× )= –4;
(2)
素养考点 1
有理数除法的运算
探究新知
答案:(1)–4
(2)–8
(3)0
1.计算:
巩固练习
(4)
(1)24 ÷(-6)
(2)(-4) ÷
(3)0÷
(4)( ) ÷( )
例2 化简下列各式:
素养考点 2
有理数的化简
探究新知
(1) ;(2) .
解:(1)
(2)
2. 化简:
(1) = ÷ = .
(2) = = = .
(3) = _____.
–8
(–72)
9
(–30)÷(–45)
0
30÷45
巩固练习
例3 计算
(1) (2)
解:(1)原式=
=
=
=
=
有理数的乘除混合运算
知识点 2
探究新知
如果有带分数,可以将带分数写成整数部分和分数部分的和,利用分配律进行运算,更加简便.
(2)原式=
= 1
将小数化为分数
1. 有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
2. 乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算).
探究新知
归纳总结
(1)
(2)
解:原式=
=
=
解:原式=
=
=
=
3.计算
巩固练习
2. 计算:(–12) ÷ 3= .
连接中考
1. (–21) ÷7的结果是( )
A.3 B.–3 C. D. –
B
–4
巩固练习
1. 计算 2. 计算
基础巩固题
课堂检测
解:原式=
=
解:原式=
=
3. 计算
解:原式=
=
填空:
(1)若a,b互为相反数,且a ≠ b,则 =________;
(2)当a < 0时, =_______;
(3)若 ,则a,b的符号分别是__________.
(4)若–3x=12,则x =_____.
能力提升题
课堂检测
-4
若|2x+6|+|3–y|=0,则 = .
解析:由题意得,|2x+6|=0, |3–y|=0,
解得x = –3, y=3, 所以 = –1.
拓广探索题
课堂检测
–1
有理数的乘除运算
有理数除法法则
有理数乘除的转化
有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
乘除混合运算
乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算).
课堂小结
1.
2. 两数相除,同号得正,异号得负,并把绝对值相除. 0除以任何一个不等于0的数,都得0 .
数字入诗
明代南海才子伦文叙为苏东坡《百鸟归巢图》题的数学诗:
天生一只又一只,三四五六七八只。
凤凰何少鸟何多,啄尽人间千石谷!
诗中数字:一只又一只,
三四五六七八只。
请问何来百鸟呢
导入新知
在这些数中加上适当的运算符号就能得到100.
1+1+3×4+5×6+7×8=100
导入新知
诗中数字:一只又一只,
三四五六七八只。
1.掌握有理数加减乘除混合运算的顺序,能熟练地进行有理数加减乘除混合运算.
2.会用计算器进行有理数的加减乘除运算,会运用有理数的四则运算解决实际问题.
素养目标
问题1:小学的四则混合运算的顺序是怎样的?
先乘除,后加减,同级运算从左至右,有括号先算括号内,再算括号外. 括号计算顺序:先小括号,再中括号,最后大括号.
有理数的加减乘除混合运算
知识点 1
探究新知
问题2:我们目前都学习了哪些运算?
加法、减法、乘法、除法.
一个运算中,含有有理数的加、减、乘、除等多种运算,称为有理数的混合运算.
探究新知
探究1:下列式子含有哪几种运算?先算什么,后算什么?
加减运算
第一级运算
乘除运算
第二级运算
探究新知
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
有理数混合运算的顺序:
探究2:观察式子 ,应该按照什么顺序
来计算?
探究新知
归纳总结
(1)原式= 6–4=2
解:
(2)原式= –6 – 150= – 156
(3)原式= –28+3= –25
素养考点 1
有理数的混合运算
例1 计算:
(1)
(2)
(3)
探究新知
1.计算:
(1) ;(2) .
解析:先算括号里面的→除法转化为乘法→计算→结果.
巩固练习
解:(1)原式=
=
=
(2)原式=
=
=
=
例2 计算 .
按常规方法计算
解:方法一,
原式=
=
=
素养考点 2
有理数混合运算的简便计算
探究新知
= .
简便计算,先取倒数
方法二,
原式的倒数为
=
故
探究新知
=
=
解:原式的倒数为
故
2. 选择合适的方法计算:
巩固练习
例3 某公司去年1~3月平均每月亏损1.5万元,4~6月平均盈利2万元,7~10月平均盈利1.7万元,11~12月平均亏损2.3万元,这个公司去年总盈亏情况如何?
有理数混合运算的应用
素养考点 3
探究新知
解:记盈利额为正数,亏损额为负数,公司去年全年总的盈亏(单位:万元)为
(–1.5)×3+2×3+1.7×4+(–2.3)×2
= –4.5+6+6.8 –4.6
=3.7(万元)
答:这个公司去年全年盈利3.7万元.
3.一架直升飞机从高度为450m的位置开始,先以20m/s的速度上升60s,后以12m/s的速度下降120s,这时直升机所在的高度是多少?
解:450+20×60–12×120
=450+1200–1440
=210(m)
答:这时直升机所在的高度是210m.
巩固练习
利用计算器进行有理数的混合运算
知识点 2
1.计算器是一种方便实用的计算工具,用计算器进行比较复杂的数的计算比笔算要快捷得多.
2.提倡在明确算理的情况下,恰当地使用计算器进行一些比较复杂的有理数加减乘除法混合运算.
探究新知
【思考】如何用计数器进行有理数的混合运算 你会使用计算器计算
在用计算器进行有理数除法运算时,如果先确定商的符号,那么只需用计算器计算商的绝对值,可以减少按键的次数(对比有理数的乘法运算).
1
(–1.5)×3+2×3+1.7×4+(–2.3)×2吗?
(–)
如果计算器带符号键 ,
只需按键:
(–)
·
7
1
+
3
×
5
·
4
+
2
×
(–)
·
3
×
2
2
×
3
+
探究新知
1.某地某天的最高气温是6℃,最低气温是–4℃,则该地当天的温差为 ℃.
连接中考
2.计算的结果是( )
A.0 B.1 C.–1 D.
A
10
巩固练习
1.下列各式中,结果相等的是( )
A. 6÷(3×2)和 6÷3×2
B. (–120+400)÷20和–120+400÷20
C. –3–(4–7)和–3–4–7
D. –4×(2÷8)和 –4×2÷8
基础巩固题
课堂检测
D
(1)23×(–5)–(–3)÷
(2)–7×(–3)×(–0.5)+(–12)×(–2.6)
20.7
2.计算:
课堂检测
13
基础巩固题
(1)2×(–3÷)–4×(–3)+15;
(2)–8+(–3)×[–4÷(– )+2]–32÷(–2).
解:(1)原式=2×(–27)–(–12)+15
= –54+12+15
= –27
= –8+(–3)×18 –(–4.5)
(2)原式= –8+(–3)×(16+2)–9÷(–2)
= –8 –54+4.5
= –57.5
课堂检测
3.计算:
基础巩固题
解:原式=
阅读下面的解题过程:
计算
=(–15)÷(–25)
=
回答:(1)上面解题过程中有两处错误,
第一处错误是第 步,错误原因是_____________;
第二处错误是第 步,错误原因是_____________ .
(第一步)
(第二步)
(第三步)
二
运算顺序有误
三
结果有误
能力提升题
课堂检测
(2)写正确的解题过程.
解:
课堂检测
一天,小红与小莉利用温差测量山峰的高度,小红在山顶测得温度是–1℃,小莉此时在山脚测得温度是5℃. 已知该地区高度每增加100米,气温大约降低0.8℃,这个山峰的高度为多少 (山脚海拔0米)
拓广探索题
课堂检测
=6÷0.8×100
=750(米)
答: 这个山峰的高度为750米.
[5–(–1)]÷0.8×100
解:依题意得
课堂检测
有理数的加减乘除混合运算顺序
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
课堂小结
