2021-2022学年人教版九年级数学下册第27章 相似 单元测试(含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第27章 相似 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 880.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 07:42:28 | ||
图片预览

文档简介
人教版九下 第27章 相似 单元测试
一、选择题(共10小题)
1. 在下列各组图形中,是位似图形的有
A. 对 B. 对 C. 对 D. 对
2. 下列四组线段中,不构成比例线段的一组是
A. ,,, B. ,,,
C. ,,, D. ,,,
3. 已知 与 相似且对应周长的比为 ,则 与 的面积比为
A. B. C. D.
4. 如图,在正方形网格上有两个相似 和 ,则
A. B. C. D.
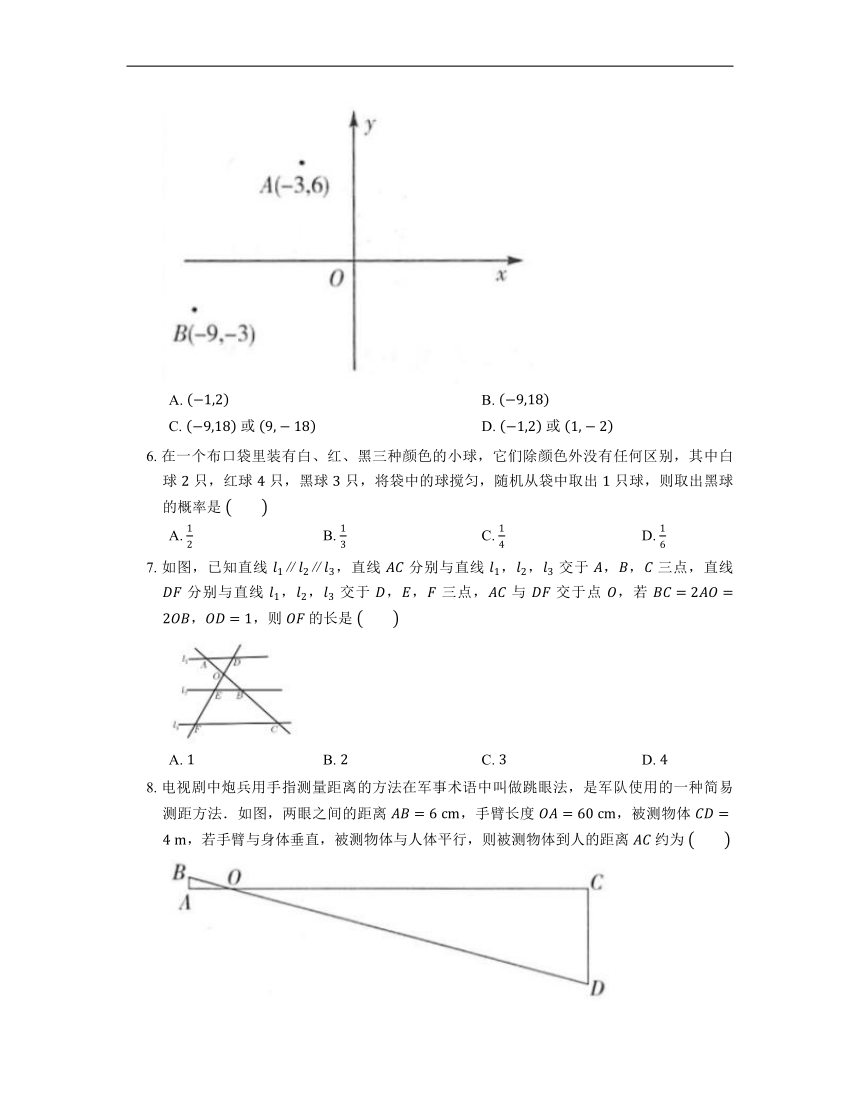
5. 如图,在平面直角坐标系中,已知点 ,,以原点 为位似中心,相似比为 ,把 缩小,则点 的对应点 的坐标是
A. B.
C. 或 D. 或
6. 在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球 只,红球 只,黑球 只,将袋中的球搅匀,随机从袋中取出 只球,则取出黑球的概率是
A. B. C. D.
7. 如图,已知直线 ,直线 分别与直线 ,, 交于 ,, 三点,直线 分别与直线 ,, 交于 ,, 三点, 与 交于点 ,若 ,,则 的长是
A. B. C. D.
8. 电视剧中炮兵用手指测量距离的方法在军事术语中叫做跳眼法,是军队使用的一种简易测距方法.如图,两眼之间的距离 ,手臂长度 ,被测物体 ,若手臂与身体垂直,被测物体与人体平行,则被测物体到人的距离 约为
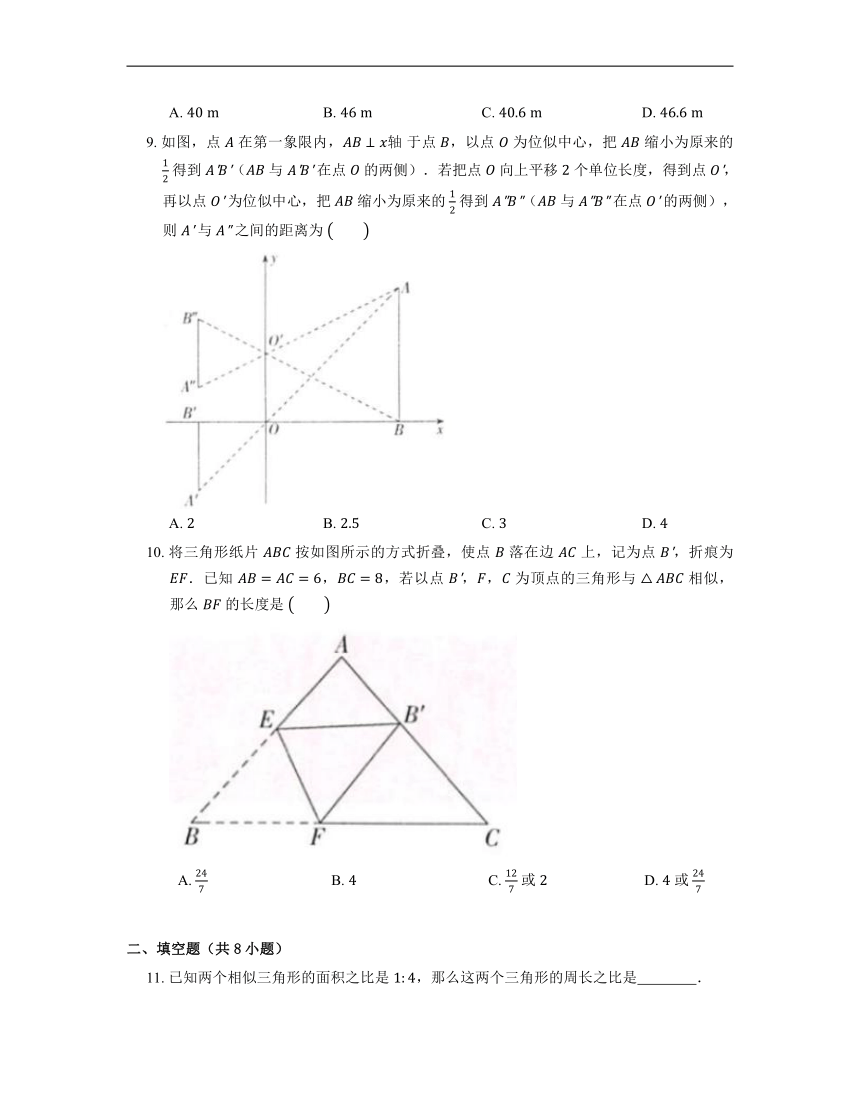
A. B. C. D.
9. 如图,点 在第一象限内, 于点 ,以点 为位似中心,把 缩小为原来的 得到 ( 与 在点 的两侧).若把点 向上平移 个单位长度,得到点 ,再以点 为位似中心,把 缩小为原来的 得到 ( 与 在点 的两侧),则 与 之间的距离为
A. B. C. D.
10. 将三角形纸片 按如图所示的方式折叠,使点 落在边 上,记为点 ,折痕为 .已知 ,,若以点 ,, 为顶点的三角形与 相似,那么 的长度是
A. B. C. 或 D. 或
二、填空题(共8小题)
11. 已知两个相似三角形的面积之比是 ,那么这两个三角形的周长之比是 .
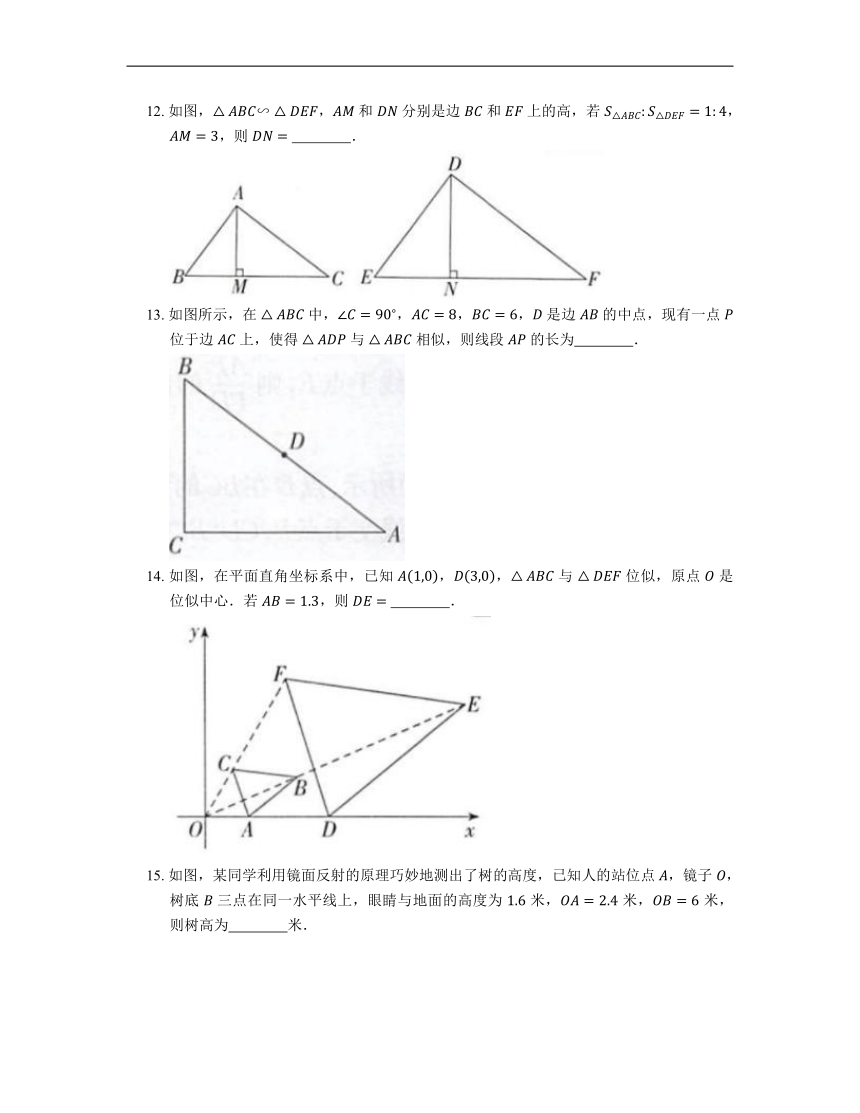
12. 如图,, 和 分别是边 和 上的高,若 ,,则 .
13. 如图所示,在 中,,,, 是边 的中点,现有一点 位于边 上,使得 与 相似,则线段 的长为 .
14. 如图,在平面直角坐标系中,已知 ,, 与 位似,原点 是位似中心.若 ,则 .
15. 如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点 ,镜子 ,树底 三点在同一水平线上,眼睛与地面的高度为 米, 米, 米,则树高为 米.
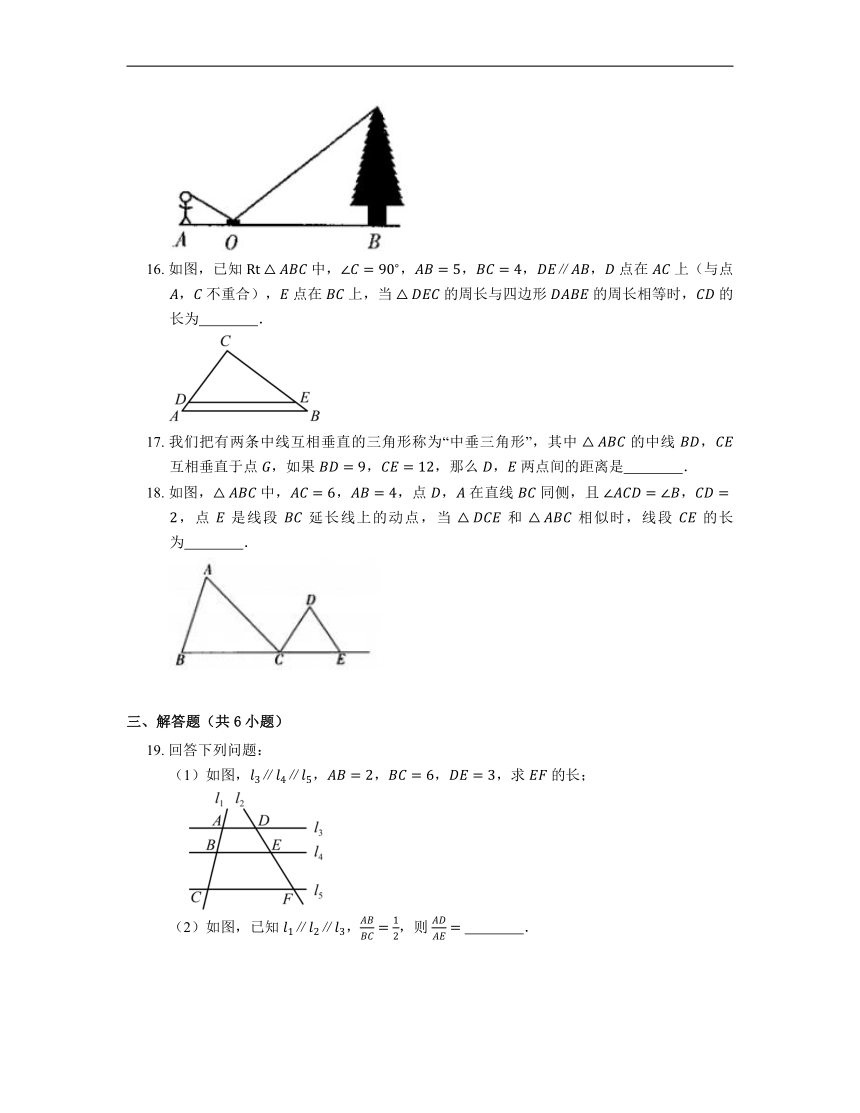
16. 如图,已知 中,,,,, 点在 上(与点 , 不重合), 点在 上,当 的周长与四边形 的周长相等时, 的长为 .
17. 我们把有两条中线互相垂直的三角形称为“中垂三角形”,其中 的中线 , 互相垂直于点 ,如果 ,,那么 , 两点间的距离是 .
18. 如图, 中,,,点 , 在直线 同侧,且 ,,点 是线段 延长线上的动点,当 和 相似时,线段 的长为 .
三、解答题(共6小题)
19. 回答下列问题:
(1)如图,,,,,求 的长;
(2)如图,已知 ,,则 .
20. 如图,在边长为 的小正方形组成的网格中,给出了格点 (顶点是网格线的交点).
()将 先向右平移 个单位,再向下平移 个单位,得到 ,画出平移后的 ;
()以 点为位似中心,在网格中画出 的位似图形 ,使它与 的相似比为 ,画出 ,并求出 的周长.
21. 如图,在 和 中,,,,, 分别为 , 的中点,求 的值.
22. 如图,小东用长为 的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距 ,与旗杆相距 ,求旗杆的高度.
23. 如图,在 中,, 于点 , 于点 .
(1)求证:;
(2)若 ,,求 的长.
24. 如图,在四边形 中,,,, 为 边上一点(不与 , 重合),连接 ,过 点作 交 于 ,使得 .
(1) 与 相似吗 为什么
(2)若 ,求 的长;
(3)当 长为多少时, 的长最大 最大为多少
答案
1. D
2. D
3. D
【解析】 与 相似以且对应周长的比为 ,
两三角形的相似比等于 ,
.
4. D
5. D
6. B
【解析】取出黑球的概率为 .
7. C
【解析】,
设 ,
,
,
,
,
,
,
.
故选C.
8. C
【解析】由题意知 ,
,
,
,,,
,
,
.
故选C.
9. C
【解析】如图,连接 ,
由题意易知 和 都与 平行,且在同一条直线上,
.
由题意知,,
,
,
,
,
,
,
.
10. D
【解析】 沿 折叠后点 和 重合,
.
设 ,则 .
要使 与 相似,只需 或 .
当 时,,
,
,,
,解得 ,即 ;
当 时,,
,即 ,解得 ,即 ,
故 .
11. (或 )
12.
【解析】,
,
,
.
13. 或
【解析】 在 中,,,,
.
是边 的中点,
.
当 时,,即 ,解得 ;
当 时,,即 ,解得 .
14.
【解析】,,
,.
与 位似,
,
,
,即 ,解得 .
15.
16.
17.
18. 或
【解析】,,
,
和 相似有两种情况:
()当 时,
,
,
;
()当 时,
,
,
.
综上所述, 的长为 或 .
19. (1) .
(2)
20. ()如图, 为所求作三角形.
()如图, 为所求作三角形.
.
21. 连接 ,,
证 ,又 ,
,
.
22. ,,,
,
,
,(),,
(),
旗杆高 米.
23. (1) ,
.
,,
,
,
.
(2) ,,
.
,,
.
,
,
,
即
(舍去负值).
24. (1) 与 相似.理由如下:
,
,
,
又 ,
.
(2) 由()知 ,
.
,,
,
,
解得 .
(3) 设 ,,则 ,
由()知 ,
,
,
,
当 时, 取最大值,最大值为 ,
当 长为 时, 的长最大,最大为 .
一、选择题(共10小题)
1. 在下列各组图形中,是位似图形的有
A. 对 B. 对 C. 对 D. 对
2. 下列四组线段中,不构成比例线段的一组是
A. ,,, B. ,,,
C. ,,, D. ,,,
3. 已知 与 相似且对应周长的比为 ,则 与 的面积比为
A. B. C. D.
4. 如图,在正方形网格上有两个相似 和 ,则
A. B. C. D.
5. 如图,在平面直角坐标系中,已知点 ,,以原点 为位似中心,相似比为 ,把 缩小,则点 的对应点 的坐标是
A. B.
C. 或 D. 或
6. 在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球 只,红球 只,黑球 只,将袋中的球搅匀,随机从袋中取出 只球,则取出黑球的概率是
A. B. C. D.
7. 如图,已知直线 ,直线 分别与直线 ,, 交于 ,, 三点,直线 分别与直线 ,, 交于 ,, 三点, 与 交于点 ,若 ,,则 的长是
A. B. C. D.
8. 电视剧中炮兵用手指测量距离的方法在军事术语中叫做跳眼法,是军队使用的一种简易测距方法.如图,两眼之间的距离 ,手臂长度 ,被测物体 ,若手臂与身体垂直,被测物体与人体平行,则被测物体到人的距离 约为
A. B. C. D.
9. 如图,点 在第一象限内, 于点 ,以点 为位似中心,把 缩小为原来的 得到 ( 与 在点 的两侧).若把点 向上平移 个单位长度,得到点 ,再以点 为位似中心,把 缩小为原来的 得到 ( 与 在点 的两侧),则 与 之间的距离为
A. B. C. D.
10. 将三角形纸片 按如图所示的方式折叠,使点 落在边 上,记为点 ,折痕为 .已知 ,,若以点 ,, 为顶点的三角形与 相似,那么 的长度是
A. B. C. 或 D. 或
二、填空题(共8小题)
11. 已知两个相似三角形的面积之比是 ,那么这两个三角形的周长之比是 .
12. 如图,, 和 分别是边 和 上的高,若 ,,则 .
13. 如图所示,在 中,,,, 是边 的中点,现有一点 位于边 上,使得 与 相似,则线段 的长为 .
14. 如图,在平面直角坐标系中,已知 ,, 与 位似,原点 是位似中心.若 ,则 .
15. 如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点 ,镜子 ,树底 三点在同一水平线上,眼睛与地面的高度为 米, 米, 米,则树高为 米.
16. 如图,已知 中,,,,, 点在 上(与点 , 不重合), 点在 上,当 的周长与四边形 的周长相等时, 的长为 .
17. 我们把有两条中线互相垂直的三角形称为“中垂三角形”,其中 的中线 , 互相垂直于点 ,如果 ,,那么 , 两点间的距离是 .
18. 如图, 中,,,点 , 在直线 同侧,且 ,,点 是线段 延长线上的动点,当 和 相似时,线段 的长为 .
三、解答题(共6小题)
19. 回答下列问题:
(1)如图,,,,,求 的长;
(2)如图,已知 ,,则 .
20. 如图,在边长为 的小正方形组成的网格中,给出了格点 (顶点是网格线的交点).
()将 先向右平移 个单位,再向下平移 个单位,得到 ,画出平移后的 ;
()以 点为位似中心,在网格中画出 的位似图形 ,使它与 的相似比为 ,画出 ,并求出 的周长.
21. 如图,在 和 中,,,,, 分别为 , 的中点,求 的值.
22. 如图,小东用长为 的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距 ,与旗杆相距 ,求旗杆的高度.
23. 如图,在 中,, 于点 , 于点 .
(1)求证:;
(2)若 ,,求 的长.
24. 如图,在四边形 中,,,, 为 边上一点(不与 , 重合),连接 ,过 点作 交 于 ,使得 .
(1) 与 相似吗 为什么
(2)若 ,求 的长;
(3)当 长为多少时, 的长最大 最大为多少
答案
1. D
2. D
3. D
【解析】 与 相似以且对应周长的比为 ,
两三角形的相似比等于 ,
.
4. D
5. D
6. B
【解析】取出黑球的概率为 .
7. C
【解析】,
设 ,
,
,
,
,
,
,
.
故选C.
8. C
【解析】由题意知 ,
,
,
,,,
,
,
.
故选C.
9. C
【解析】如图,连接 ,
由题意易知 和 都与 平行,且在同一条直线上,
.
由题意知,,
,
,
,
,
,
,
.
10. D
【解析】 沿 折叠后点 和 重合,
.
设 ,则 .
要使 与 相似,只需 或 .
当 时,,
,
,,
,解得 ,即 ;
当 时,,
,即 ,解得 ,即 ,
故 .
11. (或 )
12.
【解析】,
,
,
.
13. 或
【解析】 在 中,,,,
.
是边 的中点,
.
当 时,,即 ,解得 ;
当 时,,即 ,解得 .
14.
【解析】,,
,.
与 位似,
,
,
,即 ,解得 .
15.
16.
17.
18. 或
【解析】,,
,
和 相似有两种情况:
()当 时,
,
,
;
()当 时,
,
,
.
综上所述, 的长为 或 .
19. (1) .
(2)
20. ()如图, 为所求作三角形.
()如图, 为所求作三角形.
.
21. 连接 ,,
证 ,又 ,
,
.
22. ,,,
,
,
,(),,
(),
旗杆高 米.
23. (1) ,
.
,,
,
,
.
(2) ,,
.
,,
.
,
,
,
即
(舍去负值).
24. (1) 与 相似.理由如下:
,
,
,
又 ,
.
(2) 由()知 ,
.
,,
,
,
解得 .
(3) 设 ,,则 ,
由()知 ,
,
,
,
当 时, 取最大值,最大值为 ,
当 长为 时, 的长最大,最大为 .
