2022-2023学年人教版数学九年级上册 切线的性质与判定 专项培优练习十五(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册 切线的性质与判定 专项培优练习十五(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 465.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:24:05 | ||
图片预览




文档简介
人教版数学九年级上册专项培优练习十五
《切线的性质与判定》
一 、选择题
1.如图,AB,AC是⊙O的两条弦,∠BAC=25°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
A.25° B.30° C.35° D.40°
2.如图,线段AB是⊙O的直径,点C,D为⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠CDB等于( )
A.20° B.25° C.30° D.40°
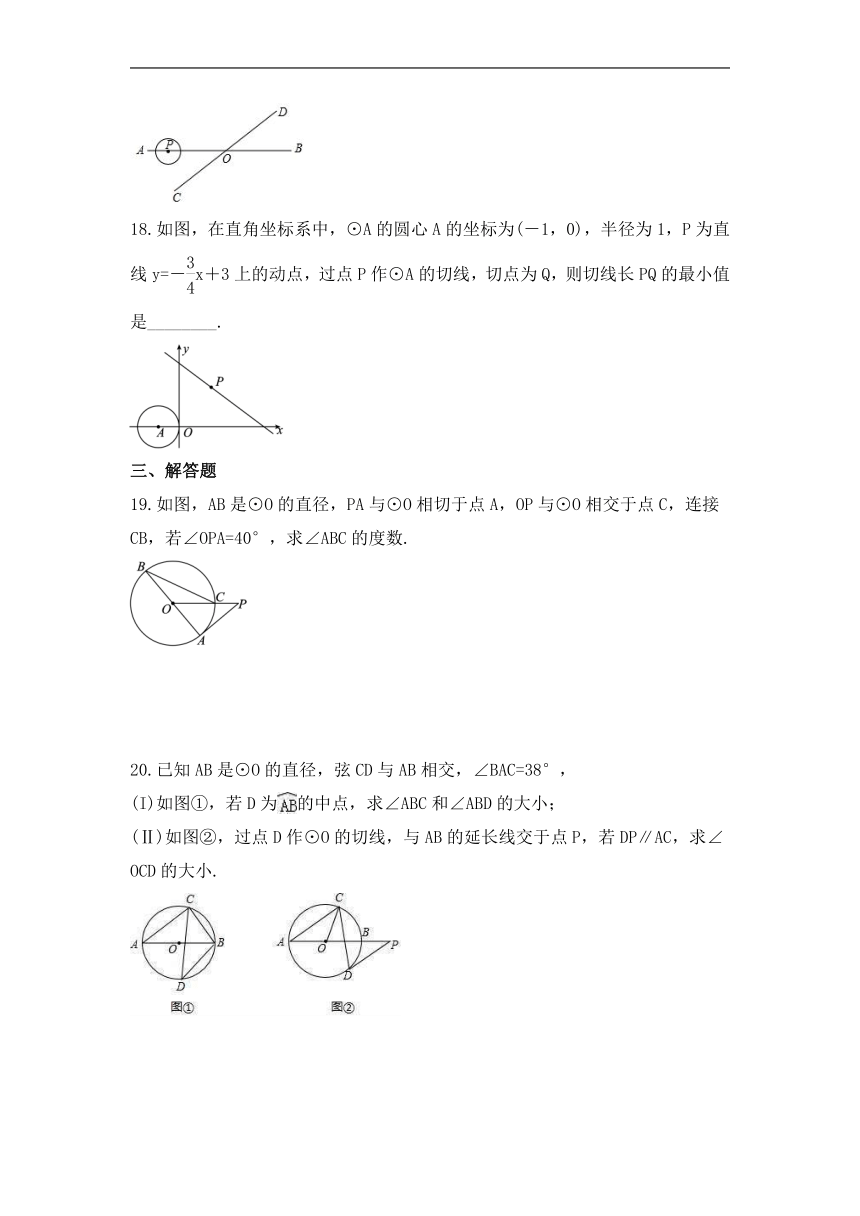
3.如图,等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为( )
A.8 B.6 C.5 D.4
4.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为( )
A.2 B. C. D.
5.如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=90°,若OA=4,则图中圆环的面积大小为( )
A.2π B.4π C.6π D.8π
6.如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面三个结论:①AD=CD;②BD=BC;③AB=2BC.其中正确结论的个数是( )
A.3 B.2 C.1 D.0
7.如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)与点C(0,16),则圆心M到坐标原点O的距离是( )
A.10 B.8 C.4 D.2
8.如图,⊙O的半径为2,P为⊙O外一点,PA切⊙O于点A,PA=2,若AB为⊙O的弦,且AB=2,则PB的长为( )
A.2 B.2 C.1或 D.2或2
9.如图,△ABC的内切圆与三边分别相切于点D、E、F,则下列等式:
① ∠EDF=∠B;
② 2∠EDF=∠A+∠C;
③ 2∠A=∠FED+∠EDF;
④ ∠AED+∠BFE+∠CDF=180°.
其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,
能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1)
11.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.-2≤b≤2
C.-212.如图,在平面直角坐标系中,⊙P与y轴相切,交直线y=x于A,B两点,已知圆心P的坐标为(2,a)(a>2),AB=2,则a的值为( )
A.4 B.2+ C. D.2+
二 、填空题
13.如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为 .
14.如图,⊙O分别切∠BAC的两边AB,AC于点E,F,点P在优弧()上,若∠BAC=66°,则∠EPF等于 度.
15.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .
16.如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设点P(x,0),则x的取值范围是____________________.
17.如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么______秒种后⊙P与直线CD相切.
18.如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,P为直线y=-x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是________.
三 、解答题
19.如图,AB是⊙O的直径,PA与⊙O相切于点A,OP与⊙O相交于点C,连接CB,若∠OPA=40°,求∠ABC的度数.
20.已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
(I)如图①,若D为的中点,求∠ABC和∠ABD的大小;
(Ⅱ)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
21.如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
22.如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
23.已知P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
24.如图,有两条公路OM,ON相交成30°角,沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿公路ON方向行驶时,在以点P为圆心,50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.已知重型运输卡车P沿公路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时,卡车P与学校A的距离;
(2)求卡车P沿公路ON方向行驶一次给学校A带来噪声影响的时间.
25.如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线
BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;
(3)求证:CD=HF.
参考答案
1.D
2.A
3.D
4.B
5.D
6.A
7.D
8.D
9.B
10.C
11.D
12.B
13.答案为:2.4
14.答案为:57°
15.答案为:5.
16.答案为:-≤x≤且x≠0
17.答案为:4或8.
18.答案为:2.
19.解:∵AB是⊙O的直径,PA与⊙O相切于点A,
∴∠BAP=90°.
∵∠OPA=40°,
∴∠AOP=180°-90°-40°=50°.
∵OB=OC,
∴∠ABC=∠BCO.
又∵∠AOP=∠ABC+∠BCO,
∴∠ABC=∠AOP=×50°=25°.
20.解:(Ⅰ)∵AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
∴∠ACB=90°,
∴∠ABC=∠ACB﹣∠BAC=90°﹣38°=52°,
∵D为的中点,∠AOB=180°,
∴∠AOD=90°,
∴∠ABD=45°;
(Ⅱ)连接OD,
∵DP切⊙O于点D,
∴OD⊥DP,即∠ODP=90°,
由DP∥AC,又∠BAC=38°,
∴∠P=∠BAC=38°,
∵∠AOD是△ODP的一个外角,
∴∠AOD=∠P+∠ODP=128°,
∴∠ACD=64°,
∵OC=OA,∠BAC=38°,
∴∠OCA=∠BAC=38°,
∴∠OCD=∠ACD﹣∠OCA=64°﹣38°=26°.
21.(1)证明:∵E是△ABC的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE
(2)证明:连接CD.
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∴ ,
∴BD=CD,
∵BD=DF,
∴CD=DB=DF,
∴∠BCF=90°,
∴BC⊥CF,
∴CF是⊙O的切线.
22.解:(1)如图,连接OD,∵AB为⊙O的直径,
∴∠ADB=90°,即∠A+∠ABD=90°,
又∵CD与⊙O相切于点D,
∴∠CDB+∠ODB=90°,
∵OD=OB,
∴∠ABD=∠ODB,
∴∠A=∠BDC;
(2)∵CM平分∠ACD,
∴∠DCM=∠ACM,
又∵∠A=∠BDC,
∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,
∵∠ADB=90°,DM=1,
∴DN=DM=1,
∴MN=.
23.解:(1)如图1,∵PQ是⊙O的切线,
∴OQ⊥PQ,
∵A是OP的中点,
∴OP=2OA,
在Rt△OPQ中,cos∠QOP==,
∴∠QOP=60°;
(2)作OD⊥BQ于D,如图2,则QD=BD,
∵∠QOP=90°,OP=4,OQ=2,
∴PQ=2,
∵∠OQD=∠PQO,
∴Rt△QOD∽Rt△QPO,
∴QD:OQ=OQ:QP,即QD:2=2:2,
∴QD=,
∴QB=2QD=.
24.解:(1)过点A作ON的垂线段,交ON于点P,如图①.
在Rt△AOP中,∠APO=90°,∠POA=30°,OA=80米,
所以AP=OA=80×=40(米),
即对学校A的噪声影响最大时,卡车P与学校A的距离是40米.
(2)以点A为圆心,50米长为半径画弧,交ON于点D,E,连接AD,AE,如图②.
在Rt△ADP中,∠APD=90°,AP=40米,AD=50米,
所以DP===30(米).同理可得EP=30米,所以DE=60米.
又因为18千米/时=5米/秒,=12(秒),
所以卡车P沿公路ON方向行驶一次给学校A带来噪声影响的时间为12秒.
25.(1)证明:(1)如图,连接OE.
∵BE⊥EF,∴∠BEF=90°,
∴BF是圆O的直径,
∴OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)证明:∵∠C=∠BHE=90°,∠EBC=∠EBA,
∴BEC=∠BEH,
∵BF是⊙O是直径,
∴∠BEF=90°,
∴∠FEH+∠BEH=90°,∠AEF+∠BEC=90°,
∴∠FEH=∠FEA,
∴FE平分∠AEH.
(3)证明:如图,连结DE.
∵BE是∠ABC的平分线,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE,
∵∠C=∠EHF=90°,
∴△CDE≌△HFE(AAS),
∴CD=HF,
《切线的性质与判定》
一 、选择题
1.如图,AB,AC是⊙O的两条弦,∠BAC=25°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
A.25° B.30° C.35° D.40°
2.如图,线段AB是⊙O的直径,点C,D为⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠CDB等于( )
A.20° B.25° C.30° D.40°
3.如图,等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为( )
A.8 B.6 C.5 D.4
4.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为( )
A.2 B. C. D.
5.如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=90°,若OA=4,则图中圆环的面积大小为( )
A.2π B.4π C.6π D.8π
6.如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线交于点C,∠A=30°,给出下面三个结论:①AD=CD;②BD=BC;③AB=2BC.其中正确结论的个数是( )
A.3 B.2 C.1 D.0
7.如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)与点C(0,16),则圆心M到坐标原点O的距离是( )
A.10 B.8 C.4 D.2
8.如图,⊙O的半径为2,P为⊙O外一点,PA切⊙O于点A,PA=2,若AB为⊙O的弦,且AB=2,则PB的长为( )
A.2 B.2 C.1或 D.2或2
9.如图,△ABC的内切圆与三边分别相切于点D、E、F,则下列等式:
① ∠EDF=∠B;
② 2∠EDF=∠A+∠C;
③ 2∠A=∠FED+∠EDF;
④ ∠AED+∠BFE+∠CDF=180°.
其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
10.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,
能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1)
11.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.-2≤b≤2
C.-2
A.4 B.2+ C. D.2+
二 、填空题
13.如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为 .
14.如图,⊙O分别切∠BAC的两边AB,AC于点E,F,点P在优弧()上,若∠BAC=66°,则∠EPF等于 度.
15.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .
16.如图,已知⊙O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设点P(x,0),则x的取值范围是____________________.
17.如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么______秒种后⊙P与直线CD相切.
18.如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,P为直线y=-x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是________.
三 、解答题
19.如图,AB是⊙O的直径,PA与⊙O相切于点A,OP与⊙O相交于点C,连接CB,若∠OPA=40°,求∠ABC的度数.
20.已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
(I)如图①,若D为的中点,求∠ABC和∠ABD的大小;
(Ⅱ)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
21.如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
22.如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
23.已知P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
24.如图,有两条公路OM,ON相交成30°角,沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿公路ON方向行驶时,在以点P为圆心,50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.已知重型运输卡车P沿公路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时,卡车P与学校A的距离;
(2)求卡车P沿公路ON方向行驶一次给学校A带来噪声影响的时间.
25.如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线
BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;
(3)求证:CD=HF.
参考答案
1.D
2.A
3.D
4.B
5.D
6.A
7.D
8.D
9.B
10.C
11.D
12.B
13.答案为:2.4
14.答案为:57°
15.答案为:5.
16.答案为:-≤x≤且x≠0
17.答案为:4或8.
18.答案为:2.
19.解:∵AB是⊙O的直径,PA与⊙O相切于点A,
∴∠BAP=90°.
∵∠OPA=40°,
∴∠AOP=180°-90°-40°=50°.
∵OB=OC,
∴∠ABC=∠BCO.
又∵∠AOP=∠ABC+∠BCO,
∴∠ABC=∠AOP=×50°=25°.
20.解:(Ⅰ)∵AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
∴∠ACB=90°,
∴∠ABC=∠ACB﹣∠BAC=90°﹣38°=52°,
∵D为的中点,∠AOB=180°,
∴∠AOD=90°,
∴∠ABD=45°;
(Ⅱ)连接OD,
∵DP切⊙O于点D,
∴OD⊥DP,即∠ODP=90°,
由DP∥AC,又∠BAC=38°,
∴∠P=∠BAC=38°,
∵∠AOD是△ODP的一个外角,
∴∠AOD=∠P+∠ODP=128°,
∴∠ACD=64°,
∵OC=OA,∠BAC=38°,
∴∠OCA=∠BAC=38°,
∴∠OCD=∠ACD﹣∠OCA=64°﹣38°=26°.
21.(1)证明:∵E是△ABC的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE
(2)证明:连接CD.
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∴ ,
∴BD=CD,
∵BD=DF,
∴CD=DB=DF,
∴∠BCF=90°,
∴BC⊥CF,
∴CF是⊙O的切线.
22.解:(1)如图,连接OD,∵AB为⊙O的直径,
∴∠ADB=90°,即∠A+∠ABD=90°,
又∵CD与⊙O相切于点D,
∴∠CDB+∠ODB=90°,
∵OD=OB,
∴∠ABD=∠ODB,
∴∠A=∠BDC;
(2)∵CM平分∠ACD,
∴∠DCM=∠ACM,
又∵∠A=∠BDC,
∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,
∵∠ADB=90°,DM=1,
∴DN=DM=1,
∴MN=.
23.解:(1)如图1,∵PQ是⊙O的切线,
∴OQ⊥PQ,
∵A是OP的中点,
∴OP=2OA,
在Rt△OPQ中,cos∠QOP==,
∴∠QOP=60°;
(2)作OD⊥BQ于D,如图2,则QD=BD,
∵∠QOP=90°,OP=4,OQ=2,
∴PQ=2,
∵∠OQD=∠PQO,
∴Rt△QOD∽Rt△QPO,
∴QD:OQ=OQ:QP,即QD:2=2:2,
∴QD=,
∴QB=2QD=.
24.解:(1)过点A作ON的垂线段,交ON于点P,如图①.
在Rt△AOP中,∠APO=90°,∠POA=30°,OA=80米,
所以AP=OA=80×=40(米),
即对学校A的噪声影响最大时,卡车P与学校A的距离是40米.
(2)以点A为圆心,50米长为半径画弧,交ON于点D,E,连接AD,AE,如图②.
在Rt△ADP中,∠APD=90°,AP=40米,AD=50米,
所以DP===30(米).同理可得EP=30米,所以DE=60米.
又因为18千米/时=5米/秒,=12(秒),
所以卡车P沿公路ON方向行驶一次给学校A带来噪声影响的时间为12秒.
25.(1)证明:(1)如图,连接OE.
∵BE⊥EF,∴∠BEF=90°,
∴BF是圆O的直径,
∴OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)证明:∵∠C=∠BHE=90°,∠EBC=∠EBA,
∴BEC=∠BEH,
∵BF是⊙O是直径,
∴∠BEF=90°,
∴∠FEH+∠BEH=90°,∠AEF+∠BEC=90°,
∴∠FEH=∠FEA,
∴FE平分∠AEH.
(3)证明:如图,连结DE.
∵BE是∠ABC的平分线,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE,
∵∠C=∠EHF=90°,
∴△CDE≌△HFE(AAS),
∴CD=HF,
同课章节目录
