2022-2023学年人教版数学九年级上册24.1.4 圆周角 专项培优练习十四(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册24.1.4 圆周角 专项培优练习十四(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:29:34 | ||
图片预览



文档简介
人教版数学九年级上册专项培优练习十四
《圆周角定理》
一 、选择题
1.如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠AOC等于( )
A.25° B.30° C.50° D.65°
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB且交AB于点E,则下列结论不成立的是( )
A.∠A=∠D B.= C.∠ACB=90° D.∠COB=3∠D
3.如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB=( )
A.80° B.90° C.100° D.无法确定
4.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是( )
A. cm B.5cm C.6cm D.10cm
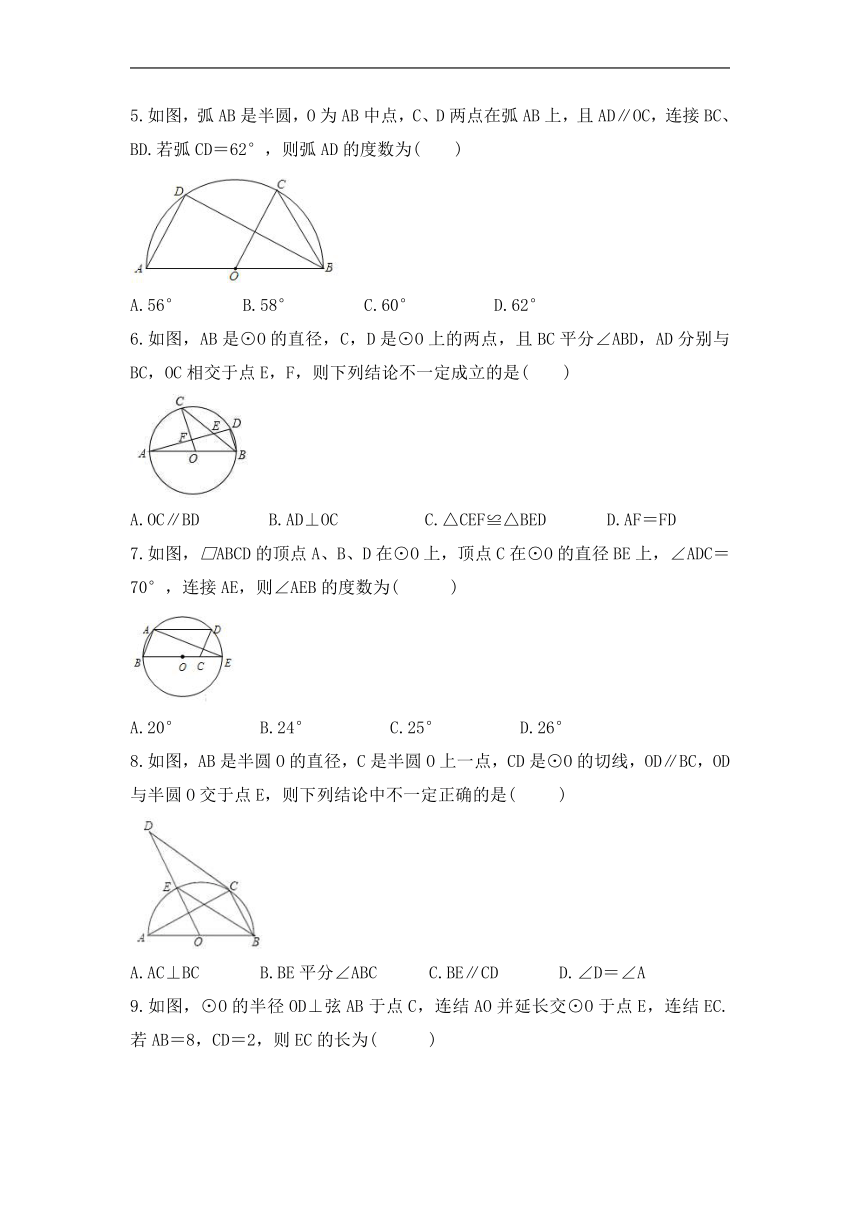
5.如图,弧AB是半圆,O为AB中点,C、D两点在弧AB上,且AD∥OC,连接BC、BD.若弧CD=62°,则弧AD的度数为( )
A.56° B.58° C.60° D.62°
6.如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A.OC∥BD B.AD⊥OC C.△CEF≌△BED D.AF=FD
7.如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接AE,则∠AEB的度数为( )
A.20° B.24° C.25° D.26°
8.如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
A.AC⊥BC B.BE平分∠ABC C.BE∥CD D.∠D=∠A
9.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2 B.8 C.2 D.2
10.在直角三角形ABC中,∠C=60°,以AB为直径的半圆交斜边BC于D,则△ACD与△ABD的面积之比为( )
A.1:2 B.1:3 C.2:3 D.3:4
11.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+ B.2+ C.4 D.2+2
12.已知点A,B,C是直径为6cm的⊙O上的点,且AB=3cm,AC=3cm,则∠BAC度数为( )
A.15° B.75°或15° C.105°或15° D.75°或105°
二 、填空题
13.如图,△ABC内接于⊙O,BA=BC,∠ACB=28°,AD为⊙O的直径,则∠DAC的度数是 .
14.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD= .
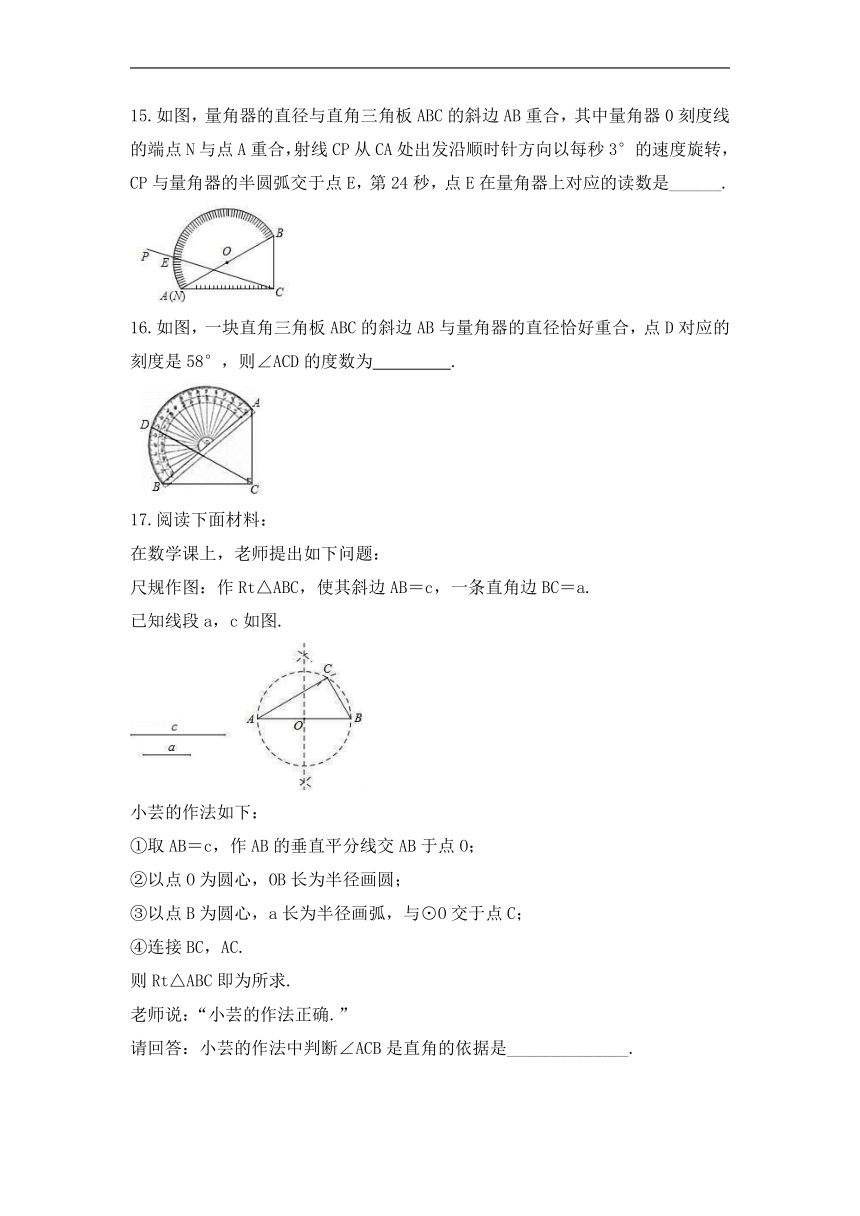
15.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是______.
16.如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为 .
17.阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.
小芸的作法如下:
①取AB=c,作AB的垂直平分线交AB于点O;
②以点O为圆心,OB长为半径画圆;
③以点B为圆心,a长为半径画弧,与⊙O交于点C;
④连接BC,AC.
则Rt△ABC即为所求.
老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是______________.
18.如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是弧BC上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为 .
三 、解答题
19.如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.
20.如图,等腰三角形ABC中,BA=BC,以AB为直径作圆,交BC于点E,圆心为O.在EB上截取ED=EC,连接AD并延长,交⊙O于点F,连接OE、EF.
(1)试判断△ACD的形状,并说明理由;
(2)求证:∠ADE=∠OEF.
21.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=13,BC﹣AC=7,求CE的长.
22.如图,在平面直角坐标系中,以M(0,2)圆心,4为半径的⊙M交x轴于A、B两点,交y轴于C、D两点,连结BM并延长交⊙M于点P,连结PC交x轴于点E.
(1)求∠DMP的度数;
(2)求△BPE的面积.
23.如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为______,CE的长是______.
24.如图,A、B是⊙O上的两个点,已知P为平面内一点,(P、A、B三点不在同一条直线上).
(1)若点P在⊙O上,⊙O的半径为1.
①当∠APB=45°时,AB的长度为 ,
②当AB=1时,∠APB= °;
(2)若点P不在⊙O上,直线PA、PB交⊙O于点C、D(点C与点A、点D与点B均不重合),连接AD,设∠CAD=α,∠ADB=β,试用α、β表示∠APB(请直接写出答案,并画出示意图).
参考答案
1.C.
2.D.
3.B.
4.B.
5.A.
6.C.
7.A.
8.C.
9.D.
10.B.
11.C.
12.C.
13.答案为:34°.
14.答案为:62°;
15.答案为:144°.
16.答案为:61°.
17.答案为:直径所对的圆周角为直角.
18.答案为:-2.
19.证明:(1)∵CD平分∠ECA,
∴∠ECD=∠DCA.
∵∠ECD+∠DCB=180°,∠DCB+∠BAD=180°,
∴∠ECD=∠DAB.
又∵∠DCA=∠DBA,
∴∠DBA=∠DAB.
∴DB=DA.
∴△ABD是等腰三角形.
(2)∵∠DCE=∠DCA=45°,
∴∠ECA=∠ACB=90°.
∴∠BDA=90°.
∴AB是直径.
∵BD=AD=6,
∴AB=6.
∴⊙O的半径为3.
20.解:(1)△ACD是等腰三角形.连接AE,
∵AB是⊙O的直径,
∴∠AED=90°,
∴AE⊥CD,
∵CE=ED,
∴AC=AD,
∴△ACD是等腰三角形;
(2)∵∠ADE=∠DEF+∠F,∠OEF=∠OED+∠DEF,
而∠OED=∠B,∠B=∠F,
∴∠ADE=∠OEF.
21.证明:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D
(2)解:设BC=x,则AC=x﹣7,
在Rt△ABC中,AC2+BC2=AB2, 即(x﹣7)2+x2=132,
解得:x1=12,x2=﹣5(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=12
22.解:(1)∵M(0,2),
∴OM=2,
在Rt△OBM中,∵MB=4,OM=2,
∴OM=BM,
∴∠OBM=30°,
∴∠BOM=60°,
∴∠DMP=∠BMO=60°;
(2)连结PA,如图,
∵PB为直径,
∴∠BPP=90°,
在Rt△PBA中,
∵∠ABP=30°,PB=8,
∴PA=PB=4,AB=PA=4,
∵OM⊥AB,
∴弧AC=弧BC,
∴∠APC=∠BOC=30°,
在Rt△PAE中,∵∠APE=30°,PA=4,
∴AE=PA=
∴BE=AB﹣AE=4﹣=,
∴△BPE的面积=×4×=.
23.(1)证明:∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠2﹦90°﹣∠ACE﹦∠A,
∵C是弧BD的中点,
∴弧BC=弧DC,
∴∠1﹦∠A(等弧所对的圆周角相等),
∴∠1﹦∠2,
∴CF﹦BF;
(2)解:∵C是弧BD的中点,CD﹦6,
∴BC=6,
∵∠ACB﹦90°,
∴AB2=AC2+BC2,
又∵BC=CD,
∴AB2=64+36=100,
∴AB=10,
∴CE=4.8,
故⊙O的半径为5,CE的长是4.8.
24.解:(1)①∵点P在⊙O上,∠APB=45°,
∴∠AOB=90°,
∵OA=OB=1,
∴AB=;
②∵AB=1,OA=OB=1,
∴△OAB是等边三角形,
∴∠AOB=90°,
若点P在优弧AB上,则∠APB=30°,
若点P在劣弧AB上,则∠APB=180°﹣30°=150°;
综上可得:∠APB=30°或150°;故答案为:①;②30°或150°;
(2)①P在圆外时,
如图①,若点C、D分别在线段PA、PB上,则∠APB=β﹣α;
如图②,若点C在线段PA的延长线上,点D在线段PB上,则∠APB=α+β﹣180°;
如图③,若点C在线段PA上,点D在线段PB的延长线上,则∠APB=180°﹣α﹣β;
如图④,若点C、D分别在线段PA、PB的延长线上,则∠APB=α﹣β;
②P在圆内时,如图⑤,∠APB=α+β.
《圆周角定理》
一 、选择题
1.如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠AOC等于( )
A.25° B.30° C.50° D.65°
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB且交AB于点E,则下列结论不成立的是( )
A.∠A=∠D B.= C.∠ACB=90° D.∠COB=3∠D
3.如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB=( )
A.80° B.90° C.100° D.无法确定
4.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是( )
A. cm B.5cm C.6cm D.10cm
5.如图,弧AB是半圆,O为AB中点,C、D两点在弧AB上,且AD∥OC,连接BC、BD.若弧CD=62°,则弧AD的度数为( )
A.56° B.58° C.60° D.62°
6.如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A.OC∥BD B.AD⊥OC C.△CEF≌△BED D.AF=FD
7.如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接AE,则∠AEB的度数为( )
A.20° B.24° C.25° D.26°
8.如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
A.AC⊥BC B.BE平分∠ABC C.BE∥CD D.∠D=∠A
9.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2 B.8 C.2 D.2
10.在直角三角形ABC中,∠C=60°,以AB为直径的半圆交斜边BC于D,则△ACD与△ABD的面积之比为( )
A.1:2 B.1:3 C.2:3 D.3:4
11.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+ B.2+ C.4 D.2+2
12.已知点A,B,C是直径为6cm的⊙O上的点,且AB=3cm,AC=3cm,则∠BAC度数为( )
A.15° B.75°或15° C.105°或15° D.75°或105°
二 、填空题
13.如图,△ABC内接于⊙O,BA=BC,∠ACB=28°,AD为⊙O的直径,则∠DAC的度数是 .
14.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD= .
15.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是______.
16.如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为 .
17.阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.
小芸的作法如下:
①取AB=c,作AB的垂直平分线交AB于点O;
②以点O为圆心,OB长为半径画圆;
③以点B为圆心,a长为半径画弧,与⊙O交于点C;
④连接BC,AC.
则Rt△ABC即为所求.
老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是______________.
18.如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是弧BC上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为 .
三 、解答题
19.如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.
20.如图,等腰三角形ABC中,BA=BC,以AB为直径作圆,交BC于点E,圆心为O.在EB上截取ED=EC,连接AD并延长,交⊙O于点F,连接OE、EF.
(1)试判断△ACD的形状,并说明理由;
(2)求证:∠ADE=∠OEF.
21.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=13,BC﹣AC=7,求CE的长.
22.如图,在平面直角坐标系中,以M(0,2)圆心,4为半径的⊙M交x轴于A、B两点,交y轴于C、D两点,连结BM并延长交⊙M于点P,连结PC交x轴于点E.
(1)求∠DMP的度数;
(2)求△BPE的面积.
23.如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为______,CE的长是______.
24.如图,A、B是⊙O上的两个点,已知P为平面内一点,(P、A、B三点不在同一条直线上).
(1)若点P在⊙O上,⊙O的半径为1.
①当∠APB=45°时,AB的长度为 ,
②当AB=1时,∠APB= °;
(2)若点P不在⊙O上,直线PA、PB交⊙O于点C、D(点C与点A、点D与点B均不重合),连接AD,设∠CAD=α,∠ADB=β,试用α、β表示∠APB(请直接写出答案,并画出示意图).
参考答案
1.C.
2.D.
3.B.
4.B.
5.A.
6.C.
7.A.
8.C.
9.D.
10.B.
11.C.
12.C.
13.答案为:34°.
14.答案为:62°;
15.答案为:144°.
16.答案为:61°.
17.答案为:直径所对的圆周角为直角.
18.答案为:-2.
19.证明:(1)∵CD平分∠ECA,
∴∠ECD=∠DCA.
∵∠ECD+∠DCB=180°,∠DCB+∠BAD=180°,
∴∠ECD=∠DAB.
又∵∠DCA=∠DBA,
∴∠DBA=∠DAB.
∴DB=DA.
∴△ABD是等腰三角形.
(2)∵∠DCE=∠DCA=45°,
∴∠ECA=∠ACB=90°.
∴∠BDA=90°.
∴AB是直径.
∵BD=AD=6,
∴AB=6.
∴⊙O的半径为3.
20.解:(1)△ACD是等腰三角形.连接AE,
∵AB是⊙O的直径,
∴∠AED=90°,
∴AE⊥CD,
∵CE=ED,
∴AC=AD,
∴△ACD是等腰三角形;
(2)∵∠ADE=∠DEF+∠F,∠OEF=∠OED+∠DEF,
而∠OED=∠B,∠B=∠F,
∴∠ADE=∠OEF.
21.证明:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D
(2)解:设BC=x,则AC=x﹣7,
在Rt△ABC中,AC2+BC2=AB2, 即(x﹣7)2+x2=132,
解得:x1=12,x2=﹣5(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=12
22.解:(1)∵M(0,2),
∴OM=2,
在Rt△OBM中,∵MB=4,OM=2,
∴OM=BM,
∴∠OBM=30°,
∴∠BOM=60°,
∴∠DMP=∠BMO=60°;
(2)连结PA,如图,
∵PB为直径,
∴∠BPP=90°,
在Rt△PBA中,
∵∠ABP=30°,PB=8,
∴PA=PB=4,AB=PA=4,
∵OM⊥AB,
∴弧AC=弧BC,
∴∠APC=∠BOC=30°,
在Rt△PAE中,∵∠APE=30°,PA=4,
∴AE=PA=
∴BE=AB﹣AE=4﹣=,
∴△BPE的面积=×4×=.
23.(1)证明:∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠2﹦90°﹣∠ACE﹦∠A,
∵C是弧BD的中点,
∴弧BC=弧DC,
∴∠1﹦∠A(等弧所对的圆周角相等),
∴∠1﹦∠2,
∴CF﹦BF;
(2)解:∵C是弧BD的中点,CD﹦6,
∴BC=6,
∵∠ACB﹦90°,
∴AB2=AC2+BC2,
又∵BC=CD,
∴AB2=64+36=100,
∴AB=10,
∴CE=4.8,
故⊙O的半径为5,CE的长是4.8.
24.解:(1)①∵点P在⊙O上,∠APB=45°,
∴∠AOB=90°,
∵OA=OB=1,
∴AB=;
②∵AB=1,OA=OB=1,
∴△OAB是等边三角形,
∴∠AOB=90°,
若点P在优弧AB上,则∠APB=30°,
若点P在劣弧AB上,则∠APB=180°﹣30°=150°;
综上可得:∠APB=30°或150°;故答案为:①;②30°或150°;
(2)①P在圆外时,
如图①,若点C、D分别在线段PA、PB上,则∠APB=β﹣α;
如图②,若点C在线段PA的延长线上,点D在线段PB上,则∠APB=α+β﹣180°;
如图③,若点C在线段PA上,点D在线段PB的延长线上,则∠APB=180°﹣α﹣β;
如图④,若点C、D分别在线段PA、PB的延长线上,则∠APB=α﹣β;
②P在圆内时,如图⑤,∠APB=α+β.
同课章节目录
