2022-2023学年苏科版数学八年级上册2.4.1~2.4.2线段垂直平分线的性质和判定 专项练习(含解析)
文档属性
| 名称 | 2022-2023学年苏科版数学八年级上册2.4.1~2.4.2线段垂直平分线的性质和判定 专项练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:45:43 | ||
图片预览


文档简介
2.4.1~2.4.2线段垂直平分线的性质和判定 专项练习
-2022-2023学年苏科版数学八年级上册
主要内容:线段的垂直平分线
知识点1:线段的垂直平分线的概念以及尺规作法:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的______________ ,简称“中垂线”. 线段的垂直平分线需要满足两个条件:① 于这条线段,② 这条线段。
知识点2:线段的轴对称性:线段是轴对称图形,它有2条对称轴,线段本身所在的直线是它的一条对称轴,另一条是它的 .
知识点3:线段的垂直平分线的性质以及逆定理:
线段垂直平分线上的点到线段 的距离相等;
到线段 距离相等的点在线段的垂直平分线上.
一、选择题
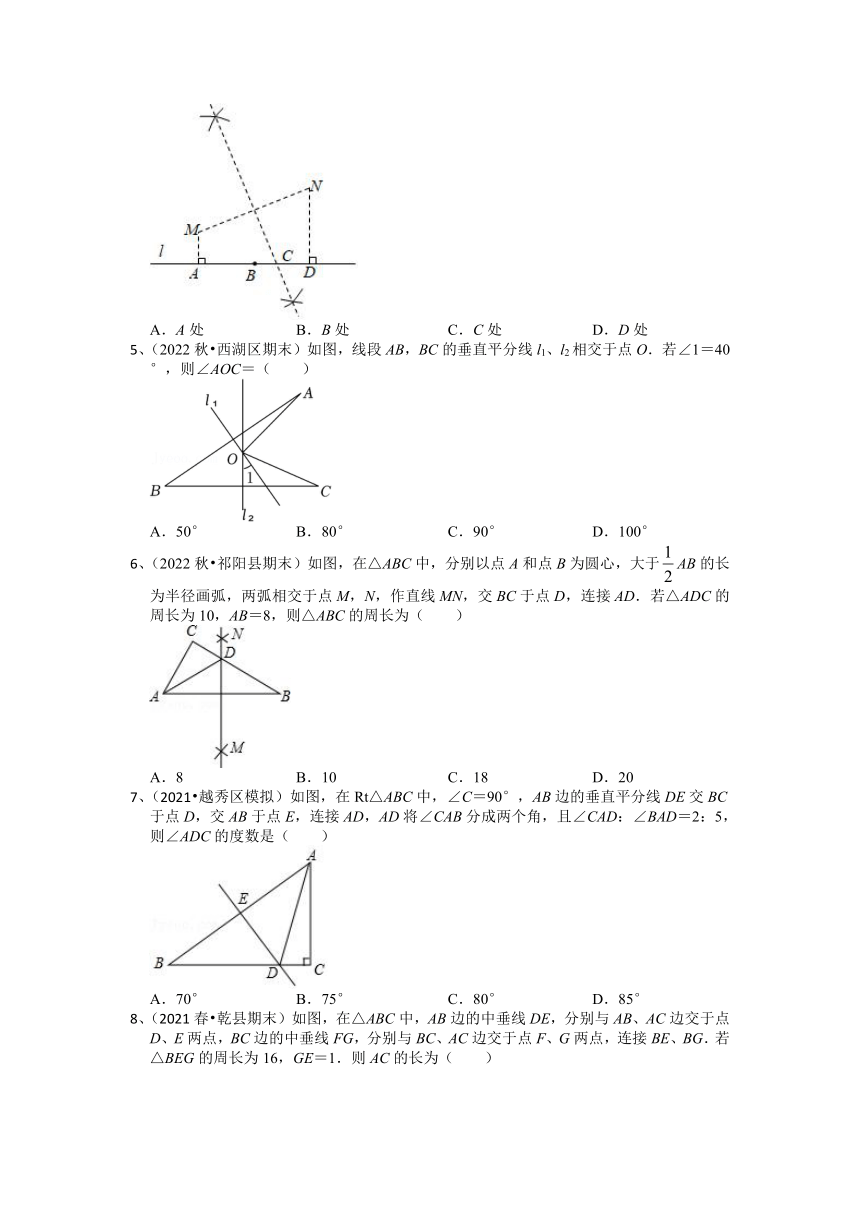
1、(2022·山东省青岛第六十三中学八年级期中)如图,在△ABC中,分别以点A和点B为圆心,大于 长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,交AB于点E,连接AD.若△ADC的周长为12,△ABC的周长为20,则AE的长为( )
A.8 B.10 C.4 D.6
2、(2022·浙江·临海市书生实验学校八年级开学考试)已知△ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
A.B.C.D.
3、(2022春 浑南区期末)有A、B、C三个不在同一直线上的居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在( )
A.△ABC的三条中线的交点处 B.△ABC三边的垂直平分线的交点处
C.△ABC三条角平分线的交点处 D.△ABC三条高所在直线的交点处
4、(2022秋 甘井子区期末)如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )
A.A处 B.B处 C.C处 D.D处
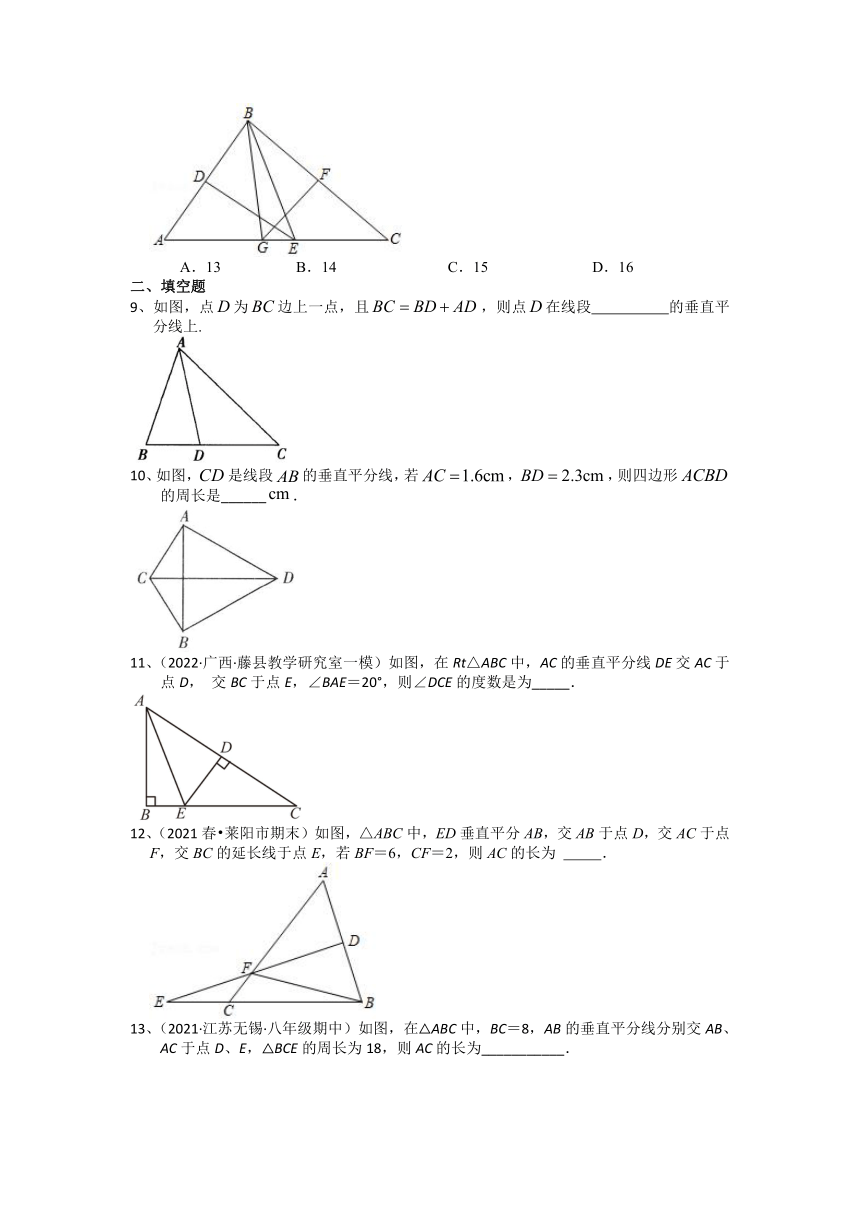
5、(2022秋 西湖区期末)如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠1=40°,则∠AOC=( )
A.50° B.80° C.90° D.100°
6、(2022秋 祁阳县期末)如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=8,则△ABC的周长为( )
A.8 B.10 C.18 D.20
7、(2021 越秀区模拟)如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
A.70° B.75° C.80° D.85°
8、(2021春 乾县期末)如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )
A.13 B.14 C.15 D.16
二、填空题
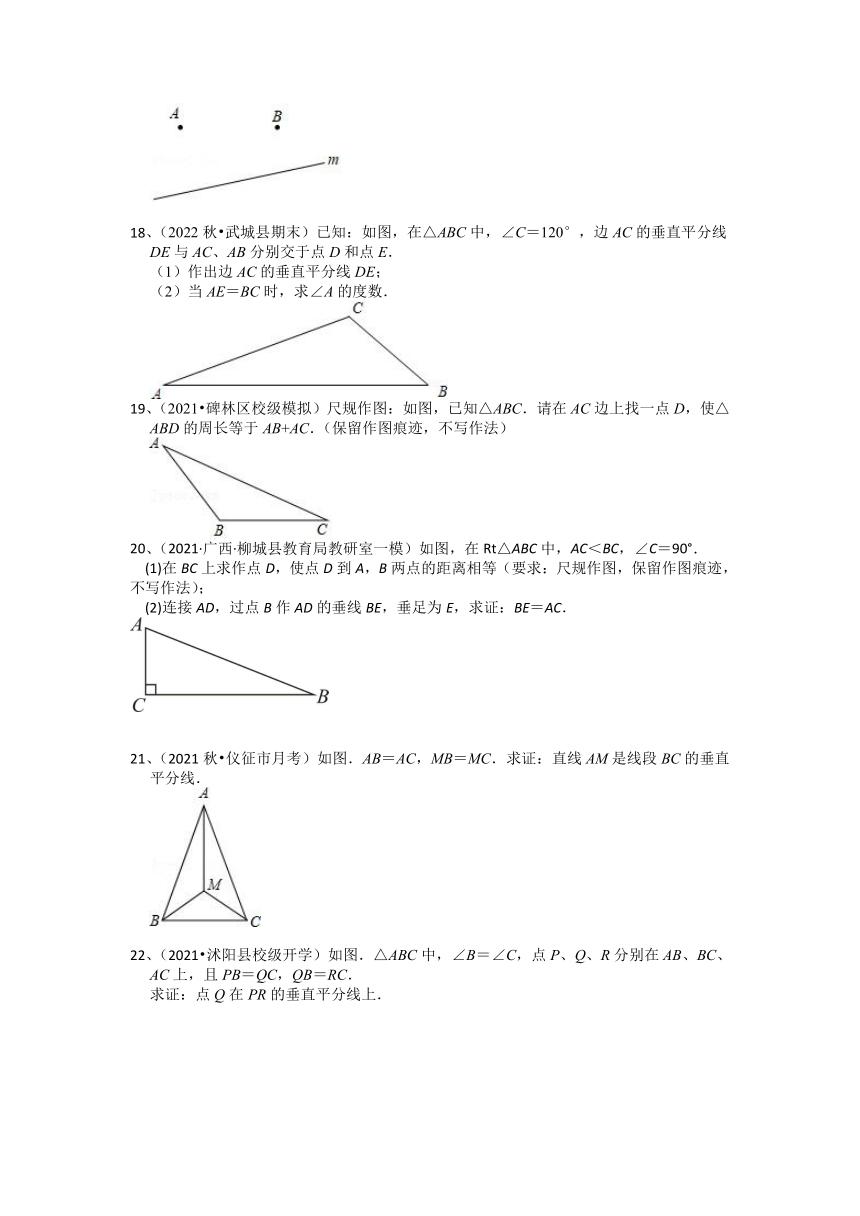
9、如图,点为边上一点,且,则点在线段 的垂直平分线上.
10、如图,是线段的垂直平分线,若,,则四边形的周长是______.
11、(2022·广西·藤县教学研究室一模)如图,在Rt△ABC中,AC的垂直平分线DE交AC于点D, 交BC于点E,∠BAE=20°,则∠DCE的度数是为_____.
12、(2021春 莱阳市期末)如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC的延长线于点E,若BF=6,CF=2,则AC的长为 .
13、(2021·江苏无锡·八年级期中)如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长为___________.
14、(2022·湖南邵阳·八年级期末)如图,线段CD与线段BE互相垂直平分,,,则______.
15、(2022·广西·环江毛南族自治县教研室八年级期末)如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点,若AB=5,AC=4,BC=6,则△APC周长的最小值是________.
16、如图,△ABC中∠BAC=60°,将△ACD沿AD折叠,使得点C落在AB上的点C′处,连接C′D与C′C,∠ACB的角平分线交AD于点E;如果BC′=DC′;那么下列结论:①∠1=∠2;②AD垂直平分C′C;
③∠B=3∠BCC′;④DC'∥EC;其中正确的是:________;(只填写序号)
三、解答题
17、(2021春 长安区期末)尺规作图(保留作图痕迹,不写作法):
如图,直线m表示一条公路,A、B表示两所大学,要在公路旁修建一个车站P,使车站到两所大学的距离相等.
(1)请用尺规在图上找出点P;
(2)请说明你作图的依据.
18、(2022秋 武城县期末)已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)当AE=BC时,求∠A的度数.
19、(2021 碑林区校级模拟)尺规作图:如图,已知△ABC.请在AC边上找一点D,使△ABD的周长等于AB+AC.(保留作图痕迹,不写作法)
20、(2021·广西·柳城县教育局教研室一模)如图,在Rt△ABC中,AC<BC,∠C=90°.
(1)在BC上求作点D,使点D到A,B两点的距离相等(要求:尺规作图,保留作图痕迹,不写作法);
(2)连接AD,过点B作AD的垂线BE,垂足为E,求证:BE=AC.
21、(2021秋 仪征市月考)如图.AB=AC,MB=MC.求证:直线AM是线段BC的垂直平分线.
22、(2021 沭阳县校级开学)如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
求证:点Q在PR的垂直平分线上.
23、(2020秋 渑池县期末)在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 .
(2)求BC的长.
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
24、(2021春 平顶山期中)如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:
(1)AE=DE;
(2)EM=EC.
25、(2022秋 鄂托克旗期中)如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.
26、(2022秋 庐阳区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.
27、(2022 阜宁县校级月考)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,求△ADE的周长;
(2)设直线DM、EN交于点O.
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数.
2.4.1~2.4.2线段垂直平分线的性质和判定 专项练习
-2022-2023学年苏科版数学八年级上册
主要内容:线段的垂直平分线
知识点1:线段的垂直平分线的概念以及尺规作法:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的______________ ,简称“中垂线”. 线段的垂直平分线需要满足两个条件:① 于这条线段,② 这条线段。
知识点2:线段的轴对称性:线段是轴对称图形,它有2条对称轴,线段本身所在的直线是它的一条对称轴,另一条是它的 .
知识点3:线段的垂直平分线的性质以及逆定理:
线段垂直平分线上的点到线段 的距离相等;
到线段 距离相等的点在线段的垂直平分线上.
一、选择题
1、(2022·山东省青岛第六十三中学八年级期中)如图,在△ABC中,分别以点A和点B为圆心,大于 长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,交AB于点E,连接AD.若△ADC的周长为12,△ABC的周长为20,则AE的长为( )
A.8 B.10 C.4 D.6
【答案】C
【详解】解:由题意得:是的垂直平分线,,
的周长为12,,,
又的周长为20,,解得,
,故选:C.
2、(2022·浙江·临海市书生实验学校八年级开学考试)已知△ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
A.B.C.D.
【答案】B
【详解】解:∵PB+PC=BC,而PA+PC=BC,∴PA=PB,
∴点P在AB的垂直平分线上,即点P为AB的垂直平分线与BC的交点.故选:B.
3、(2022春 浑南区期末)有A、B、C三个不在同一直线上的居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在( )
A.△ABC的三条中线的交点处 B.△ABC三边的垂直平分线的交点处
C.△ABC三条角平分线的交点处 D.△ABC三条高所在直线的交点处
【解答】解:∵线段垂直平分线的点到线段两段点的距离相等,
∴△ABC三边的垂直平分线的交点到三角形三个顶点的距离相等.故选:B.
4、(2022秋 甘井子区期末)如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )
A.A处 B.B处 C.C处 D.D处
【解答】解:根据作图可知:EF是线段MN的垂直平分线,
所以EF上的点到M、N的距离相等,即发射塔应该建在C处,故选:C.
5、(2022秋 西湖区期末)如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠1=40°,则∠AOC=( )
A.50° B.80° C.90° D.100°
【解答】解:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,∴∠ABC=∠1=40°,
∵OA=OB=OC,∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×40°=80°;故选:B.
6、(2022秋 祁阳县期末)如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=8,则△ABC的周长为( )
A.8 B.10 C.18 D.20
解:∵在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.
∴MN是AB的垂直平分线,∴AD=BD,
∵△ADC的周长为10,∴AC+AD+CD=AC+BD+CD=AC+BC=10,
∵AB=8,∴△ABC的周长为:AC+BC+AB=10+8=18.
故选:C.
7、(2021 越秀区模拟)如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
A.70° B.75° C.80° D.85°
【解答】解:设∠CAD=2x°,∠BAD=5x°,
∵AB的垂直平分线是DE,∴BD=AD,∴∠BAD=∠B,即∠B=5x°,
∵∠C=90°,∴∠CAB+∠B=90°,∴2x+5x+5x=90,解得:x=,即∠B=∠BAD=()°,
∴∠ADC=∠B+∠BAD=()°+()°=75°,故选:B.
8、(2021春 乾县期末)如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )
A.13 B.14 C.15 D.16
【解答】解:∵DE是线段AB的中垂线,GF是线段BC的中垂线,∴EB=EA,GB=GC,
∵△BEG周长为16,∴EB+GB+EG=16,∴EA+GC+EG=16,
∴GA+EG+EG+EG+EC=16,∴AC+2EG=16,
∵EG=1,∴AC=14,故选:B.
二、填空题
9、如图,点为边上一点,且,则点在线段 的垂直平分线上.
【答案】AC
10、如图,是线段的垂直平分线,若,,则四边形的周长是______.
【答案】7.8
【解析】解:∵CD垂直平分线段BA
∴AD=DB=2.3,BC=AC=1.6
∴四边形ABCD的周长=AD+DB+BC+CA=7.8cm.
故答案为:7.8.
11、(2022·广西·藤县教学研究室一模)如图,在Rt△ABC中,AC的垂直平分线DE交AC于点D, 交BC于点E,∠BAE=20°,则∠DCE的度数是为_____.
【答案】35°
【详解】在Rt△ABC中,,,
,,
AC的垂直平分线DE交AC于点D,,,故答案为:35°.
12、(2021春 莱阳市期末)如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC的延长线于点E,若BF=6,CF=2,则AC的长为 .
【解答】解:∵ED垂直平分AB,BF=6,∴AF=BF=6,
∵CF=2,∴AC=AF+CF=6+2=8,故答案为:8.
13、(2021·江苏无锡·八年级期中)如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长为___________.
【答案】10
解:∵DE是AB的垂直平分线,∴EA=EB,
∵△BCE的周长为18,∴BC+CE+BE=BC+CE+AE=BC+AC=18,
∵BC=8,∴AC=10,故答案为:10.
14、(2022·湖南邵阳·八年级期末)如图,线段CD与线段BE互相垂直平分,,,则______.
【答案】72°
【详解】解:∵线段CD与线段BE互相垂直平分,∴,∴,
∵,∴,∴,
∴,即:,
∵线段CD与线段BE互相垂直平分,∴AC=AD,∴,
∴.故答案为:72°.
15、(2022·广西·环江毛南族自治县教研室八年级期末)如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点,若AB=5,AC=4,BC=6,则△APC周长的最小值是________.
解:直线m与AB的交点为P,
∵直线m是BC边的垂直平分线, ∴BP=CP,∴AP+PC=BP+AP=AB,此时AP+PC值最小,
∴△APC的周长=AP+PC+AC=AB+AC,此时△APC的周长有最小值为AB+AC,
∵AB=5,AC=4,∴△APC周长的最小值为9,故答案为:9.
16、如图,△ABC中∠BAC=60°,将△ACD沿AD折叠,使得点C落在AB上的点C′处,连接C′D与C′C,∠ACB的角平分线交AD于点E;如果BC′=DC′;那么下列结论:①∠1=∠2;②AD垂直平分C′C;
③∠B=3∠BCC′;④DC'∥EC;其中正确的是:________;(只填写序号)
【答案】①②④
【解析】解:如图,∵△ACD沿AD折叠,使得点C落在AB上的点C′处,
∴∠1=∠2,A=AC,DC=D,∴AD垂直平分C′C;∴①,②都正确;
∵B=D, DC=D,
∴B=D= DC,∴∠3=∠B,∠4=∠5,
∴∠3=∠4+∠5=2∠5即∠B=2∠BC;∴③错误;
根据折叠的性质,得∠ACD=∠AD=∠B+∠3=2∠3,
∵∠ACB的角平分线交AD于点E,∴2(∠6+∠5)=2∠B,
∴ ∴D ∥EC∴④正确;
故答案为:①②④.
三、解答题
17、(2021春 长安区期末)尺规作图(保留作图痕迹,不写作法):
如图,直线m表示一条公路,A、B表示两所大学,要在公路旁修建一个车站P,使车站到两所大学的距离相等.
(1)请用尺规在图上找出点P;
(2)请说明你作图的依据.
【解答】解:(1)如图,点P即为所求.
(2)∵MN垂直平分线段AB,
∴PA=PB(线段的垂直平分线上的点到线段的两个端点的距离相等).
18、(2022秋 武城县期末)已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)当AE=BC时,求∠A的度数.
【解答】解:(1)如图所示,DE即为所求作的边AC的垂直平分线;
(2)如图,连接CE,
∵DE是AC的垂直平分线,∴AE=CE,∴∠A=∠ACE,
∵AE=BC,∴CE=BC,∴∠B=∠CEB,
设∠A=x,则∠CEB=∠A+∠ACE=x+x=2x,
在△BCE中,∠BCE=180°﹣2×2x=180°﹣4x,
∴∠ACB=∠ACE+∠BCE=x+180°﹣4x=120°,解得x=20°,即∠A=20°.
19、(2021 碑林区校级模拟)尺规作图:如图,已知△ABC.请在AC边上找一点D,使△ABD的周长等于AB+AC.(保留作图痕迹,不写作法)
【解答】解:如图,点D即为所求作.
20、(2021·广西·柳城县教育局教研室一模)如图,在Rt△ABC中,AC<BC,∠C=90°.
(1)在BC上求作点D,使点D到A,B两点的距离相等(要求:尺规作图,保留作图痕迹,不写作法);
(2)连接AD,过点B作AD的垂线BE,垂足为E,求证:BE=AC.
【解析】(1)如图,点D即为所求;
(2)由(1)得,DA=DB,∴
∵ ∴ ∴
在和中, ∴≌;∴
21、(2021秋 仪征市月考)如图.AB=AC,MB=MC.求证:直线AM是线段BC的垂直平分线.
【分析】由AB=AC,MB=MC,根据线段垂直平分线的判定定理,可得点A在BC的垂直平分线上,点M在BC的垂直平分线上,又由两点确定一条直线,可得直线AM是线段BC的垂直平分线.
【解答】证明:∵AB=AC,∴点A在BC的垂直平分线上,
∵BM=CM,∴点M在BC的垂直平分线上,
∴直线AM是BC的垂直平分线.
22、(2021 沭阳县校级开学)如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
求证:点Q在PR的垂直平分线上.
【解答】证明:连接PQ,
在△BQP和△CRQ中,, ∴△BQP≌△CRQ,
∴QP=QR,∴点Q在PR的垂直平分线上.
23、(2020秋 渑池县期末)在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 .
(2)求BC的长.
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
【解答】解:(1)∵l1是线段AB的垂直平分线,∴AD=BD,
故答案为:AD=BD;
(2)∵l2是线段AC的垂直平分线,∴EA=EC,
∵△ADE的周长为6,∴AD+DE+AE=6,∴BD+DE+EC=6,即BC=6;
(3)∵l1是线段AB的垂直平分线,∴OA=OB,
∵l2是线段AC的垂直平分线,OA=OC,∴OB=OC,
∵△OBC的周长为16,BC=6,∴OB+OC=10,∴OA=OB=OC=5.
24、(2021春 平顶山期中)如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:
(1)AE=DE;
(2)EM=EC.
【解答】证明:(1)∵DN是AB的垂直平分线,∴DA=DB,
∴∠DAB=∠B=22.5°,∴∠ADE=∠DAB+∠B=45°,
∵AE⊥BC,∴∠AED=90°,∴∠DAE=∠ADE=45°,∴AE=DE;
(2)∵DF⊥AC,AE⊥BC,∴∠MDE=∠CAE,
在△MDE和△CAE中,∴△MDE≌△CAE(ASA),∴EM=EC.
25、(2022秋 鄂托克旗期中)如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.
【解答】解:(1)∵∠ABC=∠C,∠A=40°,∴∠ABC=(180°﹣40°)÷2=70°.
∵DE是边AB的垂直平分线,∴AD=DB,∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.
(2)∵DE是边AB的垂直平分线,∴AD=DB,AE=BE,
∵△BCD的周长为18cm,∴AC+BC=AD+DC+BC=DB+DC+BC=18cm.
∵△ABC的周长为30cm,∴AB=30﹣(AC+BC)=30﹣18=12cm,∴BE=12÷2=6cm.
26、(2022秋 庐阳区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.
【解答】解:DE=BF,DE⊥BF.理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,∴AD=BD,∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,∴∠ABC=67.5°,
∴∠CBD=∠ABC﹣∠ABD=45°,∴△BCD为等腰直角三角形,∴BC=DC.
在△ECD和△FCB中,,∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,∴∠EGB=90°,即DE⊥BF.
27、(2022 阜宁县校级月考)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,求△ADE的周长;
(2)设直线DM、EN交于点O.
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数.
【解答】解:(1)∵AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE, C△ADE=AD+DE+AE=BD+DE+CE=BC=10;
(2)①如图,点O在BC的垂直平分线上,
理由:连接AO,BO,CO,
∵DM,EN分别是AB,AC的垂直平分线,∴AO=BO,OA=OC,
∴OB=OC,∴点O在BC的垂直平分线上;
②∵OM⊥AB,ON⊥AC,∴∠AMO=∠ANO=90°,
∵∠BAC=100°,∴∠MON=360°﹣90°﹣90°﹣100°=80°,
∴∠BOC=2∠MON=160°.
-2022-2023学年苏科版数学八年级上册
主要内容:线段的垂直平分线
知识点1:线段的垂直平分线的概念以及尺规作法:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的______________ ,简称“中垂线”. 线段的垂直平分线需要满足两个条件:① 于这条线段,② 这条线段。
知识点2:线段的轴对称性:线段是轴对称图形,它有2条对称轴,线段本身所在的直线是它的一条对称轴,另一条是它的 .
知识点3:线段的垂直平分线的性质以及逆定理:
线段垂直平分线上的点到线段 的距离相等;
到线段 距离相等的点在线段的垂直平分线上.
一、选择题
1、(2022·山东省青岛第六十三中学八年级期中)如图,在△ABC中,分别以点A和点B为圆心,大于 长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,交AB于点E,连接AD.若△ADC的周长为12,△ABC的周长为20,则AE的长为( )
A.8 B.10 C.4 D.6
2、(2022·浙江·临海市书生实验学校八年级开学考试)已知△ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
A.B.C.D.
3、(2022春 浑南区期末)有A、B、C三个不在同一直线上的居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在( )
A.△ABC的三条中线的交点处 B.△ABC三边的垂直平分线的交点处
C.△ABC三条角平分线的交点处 D.△ABC三条高所在直线的交点处
4、(2022秋 甘井子区期末)如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )
A.A处 B.B处 C.C处 D.D处
5、(2022秋 西湖区期末)如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠1=40°,则∠AOC=( )
A.50° B.80° C.90° D.100°
6、(2022秋 祁阳县期末)如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=8,则△ABC的周长为( )
A.8 B.10 C.18 D.20
7、(2021 越秀区模拟)如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
A.70° B.75° C.80° D.85°
8、(2021春 乾县期末)如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )
A.13 B.14 C.15 D.16
二、填空题
9、如图,点为边上一点,且,则点在线段 的垂直平分线上.
10、如图,是线段的垂直平分线,若,,则四边形的周长是______.
11、(2022·广西·藤县教学研究室一模)如图,在Rt△ABC中,AC的垂直平分线DE交AC于点D, 交BC于点E,∠BAE=20°,则∠DCE的度数是为_____.
12、(2021春 莱阳市期末)如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC的延长线于点E,若BF=6,CF=2,则AC的长为 .
13、(2021·江苏无锡·八年级期中)如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长为___________.
14、(2022·湖南邵阳·八年级期末)如图,线段CD与线段BE互相垂直平分,,,则______.
15、(2022·广西·环江毛南族自治县教研室八年级期末)如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点,若AB=5,AC=4,BC=6,则△APC周长的最小值是________.
16、如图,△ABC中∠BAC=60°,将△ACD沿AD折叠,使得点C落在AB上的点C′处,连接C′D与C′C,∠ACB的角平分线交AD于点E;如果BC′=DC′;那么下列结论:①∠1=∠2;②AD垂直平分C′C;
③∠B=3∠BCC′;④DC'∥EC;其中正确的是:________;(只填写序号)
三、解答题
17、(2021春 长安区期末)尺规作图(保留作图痕迹,不写作法):
如图,直线m表示一条公路,A、B表示两所大学,要在公路旁修建一个车站P,使车站到两所大学的距离相等.
(1)请用尺规在图上找出点P;
(2)请说明你作图的依据.
18、(2022秋 武城县期末)已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)当AE=BC时,求∠A的度数.
19、(2021 碑林区校级模拟)尺规作图:如图,已知△ABC.请在AC边上找一点D,使△ABD的周长等于AB+AC.(保留作图痕迹,不写作法)
20、(2021·广西·柳城县教育局教研室一模)如图,在Rt△ABC中,AC<BC,∠C=90°.
(1)在BC上求作点D,使点D到A,B两点的距离相等(要求:尺规作图,保留作图痕迹,不写作法);
(2)连接AD,过点B作AD的垂线BE,垂足为E,求证:BE=AC.
21、(2021秋 仪征市月考)如图.AB=AC,MB=MC.求证:直线AM是线段BC的垂直平分线.
22、(2021 沭阳县校级开学)如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
求证:点Q在PR的垂直平分线上.
23、(2020秋 渑池县期末)在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 .
(2)求BC的长.
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
24、(2021春 平顶山期中)如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:
(1)AE=DE;
(2)EM=EC.
25、(2022秋 鄂托克旗期中)如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.
26、(2022秋 庐阳区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.
27、(2022 阜宁县校级月考)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,求△ADE的周长;
(2)设直线DM、EN交于点O.
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数.
2.4.1~2.4.2线段垂直平分线的性质和判定 专项练习
-2022-2023学年苏科版数学八年级上册
主要内容:线段的垂直平分线
知识点1:线段的垂直平分线的概念以及尺规作法:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的______________ ,简称“中垂线”. 线段的垂直平分线需要满足两个条件:① 于这条线段,② 这条线段。
知识点2:线段的轴对称性:线段是轴对称图形,它有2条对称轴,线段本身所在的直线是它的一条对称轴,另一条是它的 .
知识点3:线段的垂直平分线的性质以及逆定理:
线段垂直平分线上的点到线段 的距离相等;
到线段 距离相等的点在线段的垂直平分线上.
一、选择题
1、(2022·山东省青岛第六十三中学八年级期中)如图,在△ABC中,分别以点A和点B为圆心,大于 长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,交AB于点E,连接AD.若△ADC的周长为12,△ABC的周长为20,则AE的长为( )
A.8 B.10 C.4 D.6
【答案】C
【详解】解:由题意得:是的垂直平分线,,
的周长为12,,,
又的周长为20,,解得,
,故选:C.
2、(2022·浙江·临海市书生实验学校八年级开学考试)已知△ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
A.B.C.D.
【答案】B
【详解】解:∵PB+PC=BC,而PA+PC=BC,∴PA=PB,
∴点P在AB的垂直平分线上,即点P为AB的垂直平分线与BC的交点.故选:B.
3、(2022春 浑南区期末)有A、B、C三个不在同一直线上的居民点,现要选址建一个新冠疫苗接种点方便居民接种疫苗,要求接种点到三个居民点的距离相等,接种点应建在( )
A.△ABC的三条中线的交点处 B.△ABC三边的垂直平分线的交点处
C.△ABC三条角平分线的交点处 D.△ABC三条高所在直线的交点处
【解答】解:∵线段垂直平分线的点到线段两段点的距离相等,
∴△ABC三边的垂直平分线的交点到三角形三个顶点的距离相等.故选:B.
4、(2022秋 甘井子区期末)如图,电信部门要在公路l旁修建一座移动信号发射塔.按照设计要求,发射塔到两个城镇M,N的距离必须相等,则发射塔应该建在( )
A.A处 B.B处 C.C处 D.D处
【解答】解:根据作图可知:EF是线段MN的垂直平分线,
所以EF上的点到M、N的距离相等,即发射塔应该建在C处,故选:C.
5、(2022秋 西湖区期末)如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠1=40°,则∠AOC=( )
A.50° B.80° C.90° D.100°
【解答】解:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,∴∠ABC=∠1=40°,
∵OA=OB=OC,∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×40°=80°;故选:B.
6、(2022秋 祁阳县期末)如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=8,则△ABC的周长为( )
A.8 B.10 C.18 D.20
解:∵在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.
∴MN是AB的垂直平分线,∴AD=BD,
∵△ADC的周长为10,∴AC+AD+CD=AC+BD+CD=AC+BC=10,
∵AB=8,∴△ABC的周长为:AC+BC+AB=10+8=18.
故选:C.
7、(2021 越秀区模拟)如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
A.70° B.75° C.80° D.85°
【解答】解:设∠CAD=2x°,∠BAD=5x°,
∵AB的垂直平分线是DE,∴BD=AD,∴∠BAD=∠B,即∠B=5x°,
∵∠C=90°,∴∠CAB+∠B=90°,∴2x+5x+5x=90,解得:x=,即∠B=∠BAD=()°,
∴∠ADC=∠B+∠BAD=()°+()°=75°,故选:B.
8、(2021春 乾县期末)如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )
A.13 B.14 C.15 D.16
【解答】解:∵DE是线段AB的中垂线,GF是线段BC的中垂线,∴EB=EA,GB=GC,
∵△BEG周长为16,∴EB+GB+EG=16,∴EA+GC+EG=16,
∴GA+EG+EG+EG+EC=16,∴AC+2EG=16,
∵EG=1,∴AC=14,故选:B.
二、填空题
9、如图,点为边上一点,且,则点在线段 的垂直平分线上.
【答案】AC
10、如图,是线段的垂直平分线,若,,则四边形的周长是______.
【答案】7.8
【解析】解:∵CD垂直平分线段BA
∴AD=DB=2.3,BC=AC=1.6
∴四边形ABCD的周长=AD+DB+BC+CA=7.8cm.
故答案为:7.8.
11、(2022·广西·藤县教学研究室一模)如图,在Rt△ABC中,AC的垂直平分线DE交AC于点D, 交BC于点E,∠BAE=20°,则∠DCE的度数是为_____.
【答案】35°
【详解】在Rt△ABC中,,,
,,
AC的垂直平分线DE交AC于点D,,,故答案为:35°.
12、(2021春 莱阳市期末)如图,△ABC中,ED垂直平分AB,交AB于点D,交AC于点F,交BC的延长线于点E,若BF=6,CF=2,则AC的长为 .
【解答】解:∵ED垂直平分AB,BF=6,∴AF=BF=6,
∵CF=2,∴AC=AF+CF=6+2=8,故答案为:8.
13、(2021·江苏无锡·八年级期中)如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长为___________.
【答案】10
解:∵DE是AB的垂直平分线,∴EA=EB,
∵△BCE的周长为18,∴BC+CE+BE=BC+CE+AE=BC+AC=18,
∵BC=8,∴AC=10,故答案为:10.
14、(2022·湖南邵阳·八年级期末)如图,线段CD与线段BE互相垂直平分,,,则______.
【答案】72°
【详解】解:∵线段CD与线段BE互相垂直平分,∴,∴,
∵,∴,∴,
∴,即:,
∵线段CD与线段BE互相垂直平分,∴AC=AD,∴,
∴.故答案为:72°.
15、(2022·广西·环江毛南族自治县教研室八年级期末)如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点,若AB=5,AC=4,BC=6,则△APC周长的最小值是________.
解:直线m与AB的交点为P,
∵直线m是BC边的垂直平分线, ∴BP=CP,∴AP+PC=BP+AP=AB,此时AP+PC值最小,
∴△APC的周长=AP+PC+AC=AB+AC,此时△APC的周长有最小值为AB+AC,
∵AB=5,AC=4,∴△APC周长的最小值为9,故答案为:9.
16、如图,△ABC中∠BAC=60°,将△ACD沿AD折叠,使得点C落在AB上的点C′处,连接C′D与C′C,∠ACB的角平分线交AD于点E;如果BC′=DC′;那么下列结论:①∠1=∠2;②AD垂直平分C′C;
③∠B=3∠BCC′;④DC'∥EC;其中正确的是:________;(只填写序号)
【答案】①②④
【解析】解:如图,∵△ACD沿AD折叠,使得点C落在AB上的点C′处,
∴∠1=∠2,A=AC,DC=D,∴AD垂直平分C′C;∴①,②都正确;
∵B=D, DC=D,
∴B=D= DC,∴∠3=∠B,∠4=∠5,
∴∠3=∠4+∠5=2∠5即∠B=2∠BC;∴③错误;
根据折叠的性质,得∠ACD=∠AD=∠B+∠3=2∠3,
∵∠ACB的角平分线交AD于点E,∴2(∠6+∠5)=2∠B,
∴ ∴D ∥EC∴④正确;
故答案为:①②④.
三、解答题
17、(2021春 长安区期末)尺规作图(保留作图痕迹,不写作法):
如图,直线m表示一条公路,A、B表示两所大学,要在公路旁修建一个车站P,使车站到两所大学的距离相等.
(1)请用尺规在图上找出点P;
(2)请说明你作图的依据.
【解答】解:(1)如图,点P即为所求.
(2)∵MN垂直平分线段AB,
∴PA=PB(线段的垂直平分线上的点到线段的两个端点的距离相等).
18、(2022秋 武城县期末)已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
(1)作出边AC的垂直平分线DE;
(2)当AE=BC时,求∠A的度数.
【解答】解:(1)如图所示,DE即为所求作的边AC的垂直平分线;
(2)如图,连接CE,
∵DE是AC的垂直平分线,∴AE=CE,∴∠A=∠ACE,
∵AE=BC,∴CE=BC,∴∠B=∠CEB,
设∠A=x,则∠CEB=∠A+∠ACE=x+x=2x,
在△BCE中,∠BCE=180°﹣2×2x=180°﹣4x,
∴∠ACB=∠ACE+∠BCE=x+180°﹣4x=120°,解得x=20°,即∠A=20°.
19、(2021 碑林区校级模拟)尺规作图:如图,已知△ABC.请在AC边上找一点D,使△ABD的周长等于AB+AC.(保留作图痕迹,不写作法)
【解答】解:如图,点D即为所求作.
20、(2021·广西·柳城县教育局教研室一模)如图,在Rt△ABC中,AC<BC,∠C=90°.
(1)在BC上求作点D,使点D到A,B两点的距离相等(要求:尺规作图,保留作图痕迹,不写作法);
(2)连接AD,过点B作AD的垂线BE,垂足为E,求证:BE=AC.
【解析】(1)如图,点D即为所求;
(2)由(1)得,DA=DB,∴
∵ ∴ ∴
在和中, ∴≌;∴
21、(2021秋 仪征市月考)如图.AB=AC,MB=MC.求证:直线AM是线段BC的垂直平分线.
【分析】由AB=AC,MB=MC,根据线段垂直平分线的判定定理,可得点A在BC的垂直平分线上,点M在BC的垂直平分线上,又由两点确定一条直线,可得直线AM是线段BC的垂直平分线.
【解答】证明:∵AB=AC,∴点A在BC的垂直平分线上,
∵BM=CM,∴点M在BC的垂直平分线上,
∴直线AM是BC的垂直平分线.
22、(2021 沭阳县校级开学)如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
求证:点Q在PR的垂直平分线上.
【解答】证明:连接PQ,
在△BQP和△CRQ中,, ∴△BQP≌△CRQ,
∴QP=QR,∴点Q在PR的垂直平分线上.
23、(2020秋 渑池县期末)在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 .
(2)求BC的长.
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
【解答】解:(1)∵l1是线段AB的垂直平分线,∴AD=BD,
故答案为:AD=BD;
(2)∵l2是线段AC的垂直平分线,∴EA=EC,
∵△ADE的周长为6,∴AD+DE+AE=6,∴BD+DE+EC=6,即BC=6;
(3)∵l1是线段AB的垂直平分线,∴OA=OB,
∵l2是线段AC的垂直平分线,OA=OC,∴OB=OC,
∵△OBC的周长为16,BC=6,∴OB+OC=10,∴OA=OB=OC=5.
24、(2021春 平顶山期中)如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:
(1)AE=DE;
(2)EM=EC.
【解答】证明:(1)∵DN是AB的垂直平分线,∴DA=DB,
∴∠DAB=∠B=22.5°,∴∠ADE=∠DAB+∠B=45°,
∵AE⊥BC,∴∠AED=90°,∴∠DAE=∠ADE=45°,∴AE=DE;
(2)∵DF⊥AC,AE⊥BC,∴∠MDE=∠CAE,
在△MDE和△CAE中,∴△MDE≌△CAE(ASA),∴EM=EC.
25、(2022秋 鄂托克旗期中)如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.
【解答】解:(1)∵∠ABC=∠C,∠A=40°,∴∠ABC=(180°﹣40°)÷2=70°.
∵DE是边AB的垂直平分线,∴AD=DB,∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.
(2)∵DE是边AB的垂直平分线,∴AD=DB,AE=BE,
∵△BCD的周长为18cm,∴AC+BC=AD+DC+BC=DB+DC+BC=18cm.
∵△ABC的周长为30cm,∴AB=30﹣(AC+BC)=30﹣18=12cm,∴BE=12÷2=6cm.
26、(2022秋 庐阳区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.
【解答】解:DE=BF,DE⊥BF.理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,∴AD=BD,∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,∴∠ABC=67.5°,
∴∠CBD=∠ABC﹣∠ABD=45°,∴△BCD为等腰直角三角形,∴BC=DC.
在△ECD和△FCB中,,∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,∴∠EGB=90°,即DE⊥BF.
27、(2022 阜宁县校级月考)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,求△ADE的周长;
(2)设直线DM、EN交于点O.
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数.
【解答】解:(1)∵AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE, C△ADE=AD+DE+AE=BD+DE+CE=BC=10;
(2)①如图,点O在BC的垂直平分线上,
理由:连接AO,BO,CO,
∵DM,EN分别是AB,AC的垂直平分线,∴AO=BO,OA=OC,
∴OB=OC,∴点O在BC的垂直平分线上;
②∵OM⊥AB,ON⊥AC,∴∠AMO=∠ANO=90°,
∵∠BAC=100°,∴∠MON=360°﹣90°﹣90°﹣100°=80°,
∴∠BOC=2∠MON=160°.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
