一元一次不等式与一次函数[下学期]

课件17张PPT。一元一次不等式
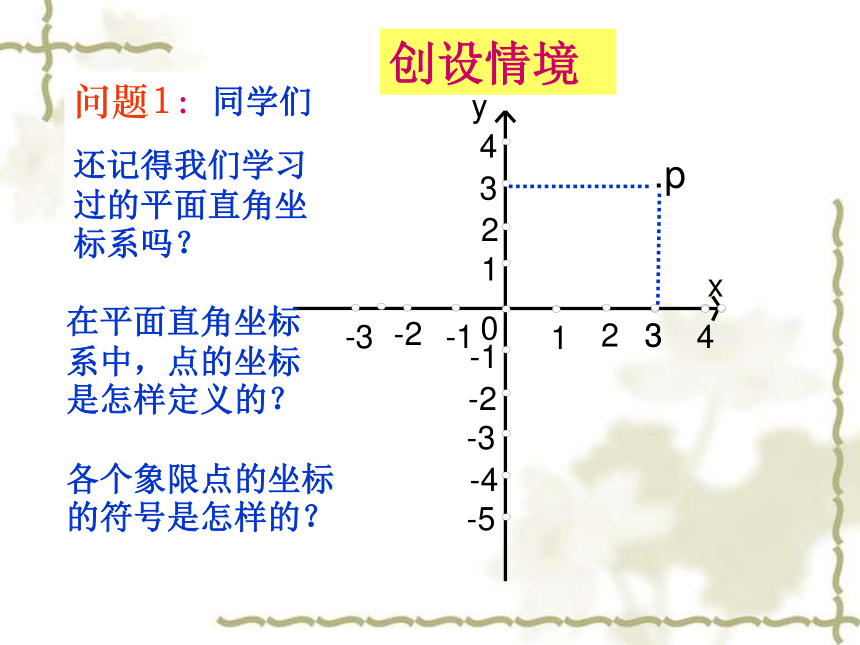
与一次函数31234-1-2-3-1-2-3-401234x-5y问题1：同学们
还记得我们学习过的平面直角坐标系吗？在平面直角坐标系中，点的坐标是怎样定义的？各个象限点的坐标的符号是怎样的？创设情境.p问题2：
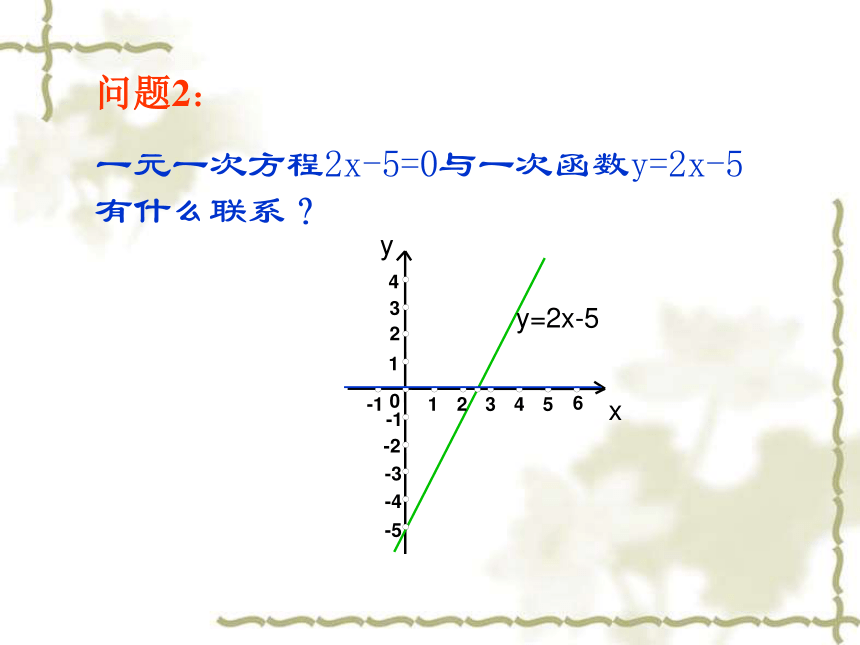
一元一次方程2x-5=0与一次函数y=2x-5有什么联系？xyy=2x-50-1-5-4-3-2-14231654321提出问题,引入新课 一元一次不等式与一次函数是怎样的关系呢？
本节课我们就来研究一元一次不等式与一次函数的关系。?xyy=2x-50-1-5-4-3-2-14231654321问题3：
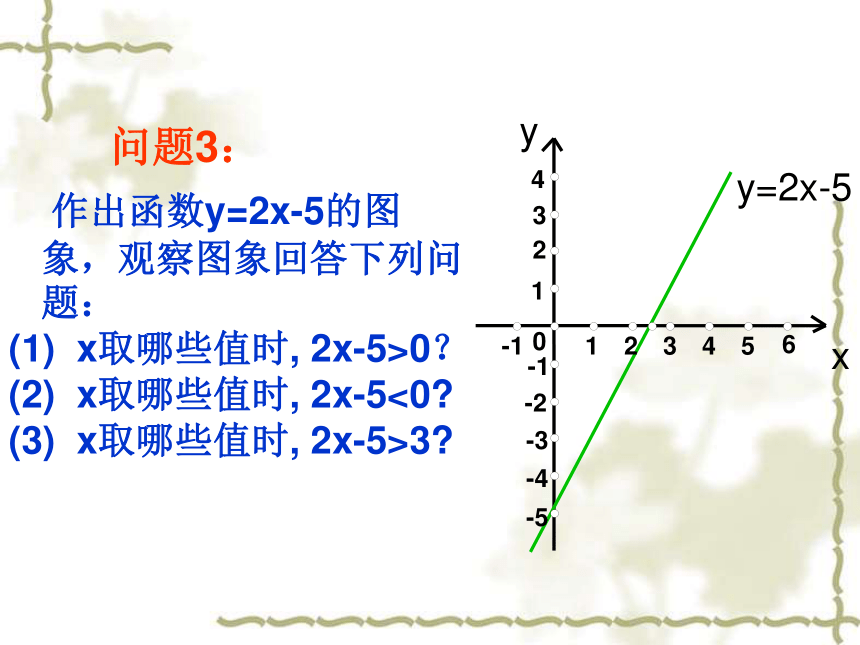
作出函数y=2x-5的图象，观察图象回答下列问题：
(1) x取哪些值时, 2x-5>0？
(2) x取哪些值时, 2x-5<0?
(3) x取哪些值时, 2x-5>3?xyy=2x-50-1-5-4-3-2-14231654321 从图象上看，
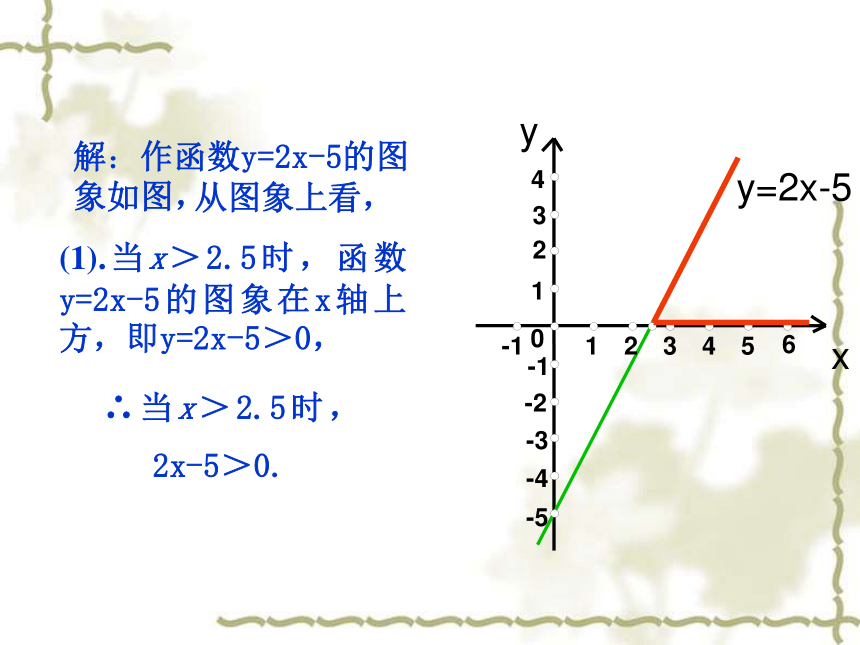
(1).当x＞2.5时，函数y=2x-5的图象在x轴上方，即y=2x-5＞0，
∴当x＞2.5时，
2x-5＞0.
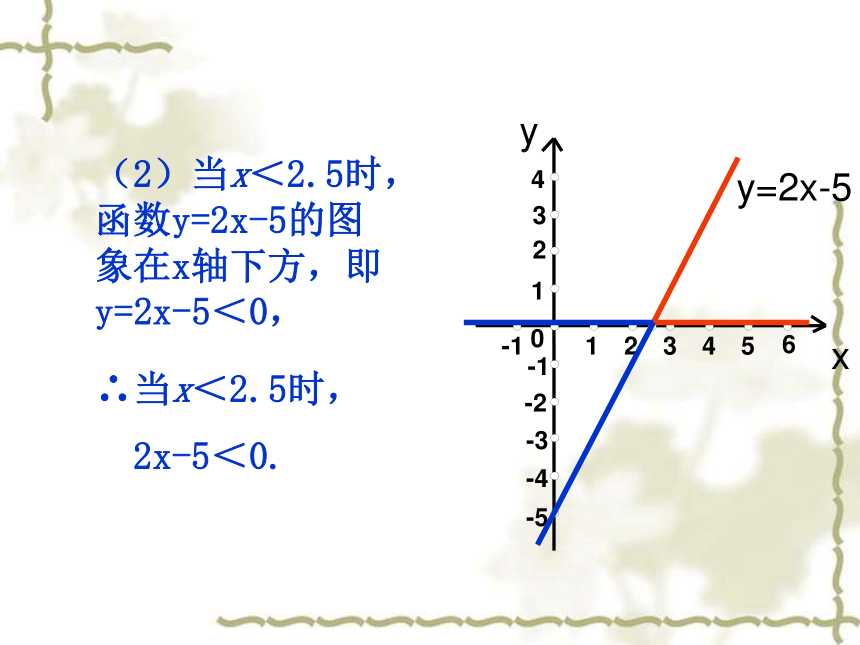
解：作函数y=2x-5的图象如图，xyy=2x-50-1-5-4-3-2-14231654321（2）当x＜2.5时，函数y=2x-5的图象在x轴下方，即y=2x-5＜0，∴当x＜2.5时，
2x-5＜0.
xyy=2x-50-1-5-4-3-2-14231654321(3).要2x-5＞3,即y＞3.过y轴上点(0,3)作x轴的平行线交y=2x-5的图象上一点B.再过点B作y轴的平行线交x轴上的一点(4,0),∴当x＞4时，
2x-5＞3BA议一议： 这三个不等式都可直接利用解不等式求得,为何要去观察图象找x的取值范围呢?
想一想： 如果y=-2x-5,
那么当x取何
值时，y>0?
解：由图可知，当x<-2.5时,y>0做一做：
兄弟俩赛跑，哥哥先让弟弟跑9m，然后自己才开始跑。已知弟弟每秒跑3m，哥哥每秒跑4m。列出函数关系式，作出函数图象，观察图象回答下列问题：
（1）何时哥哥追上弟弟？
（2）何时弟弟跑在哥哥前面？
（3）何时哥哥跑在弟弟前面？
（4）谁先跑过20m？谁先跑过100m？
(5 ) 你是怎样求解的？与同伴交流。xy-20108642100908070605040302010(s)(m)yyyy哥哥弟弟（1）何时哥哥追上弟弟？
（2）何时弟弟跑在哥哥前面？
（3）何时哥哥跑在弟弟前面？
（4）谁先跑过20m？谁先跑过100m？
(5 ) 你是怎样求解的？与同伴交流。 学以致用：
一慢车和一快车沿相同路线从A地到B地，所行的路程与时间的函数图象，如图所示，试根据图象，回答下列问题：（1）慢车比快车早出发 小时，快车追上慢车时行驶了 千米，快车比慢车早 小时到达B地。
（2）快车追上慢车需几个小时？
Y(千米） 随堂练习：
已知y1=-x+3，y2=3x-4，试确定当x分别取何值时（1）y1 >y2 ？ （2）y1 =y2 ？（3）y1 ＜y2 ？
你是怎样做的？与同伴交流。
课堂小结：作业：
课本P20 习题1.6 . 2 ,P34 , 5. 通过本节课的学习和探索，你有哪些收获和体会？
谢谢！