2023年中考数学(苏科版)总复习一轮课时训练 09 平面直角坐标系与函数(含答案)
文档属性
| 名称 | 2023年中考数学(苏科版)总复习一轮课时训练 09 平面直角坐标系与函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 329.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 10:54:58 | ||
图片预览

文档简介
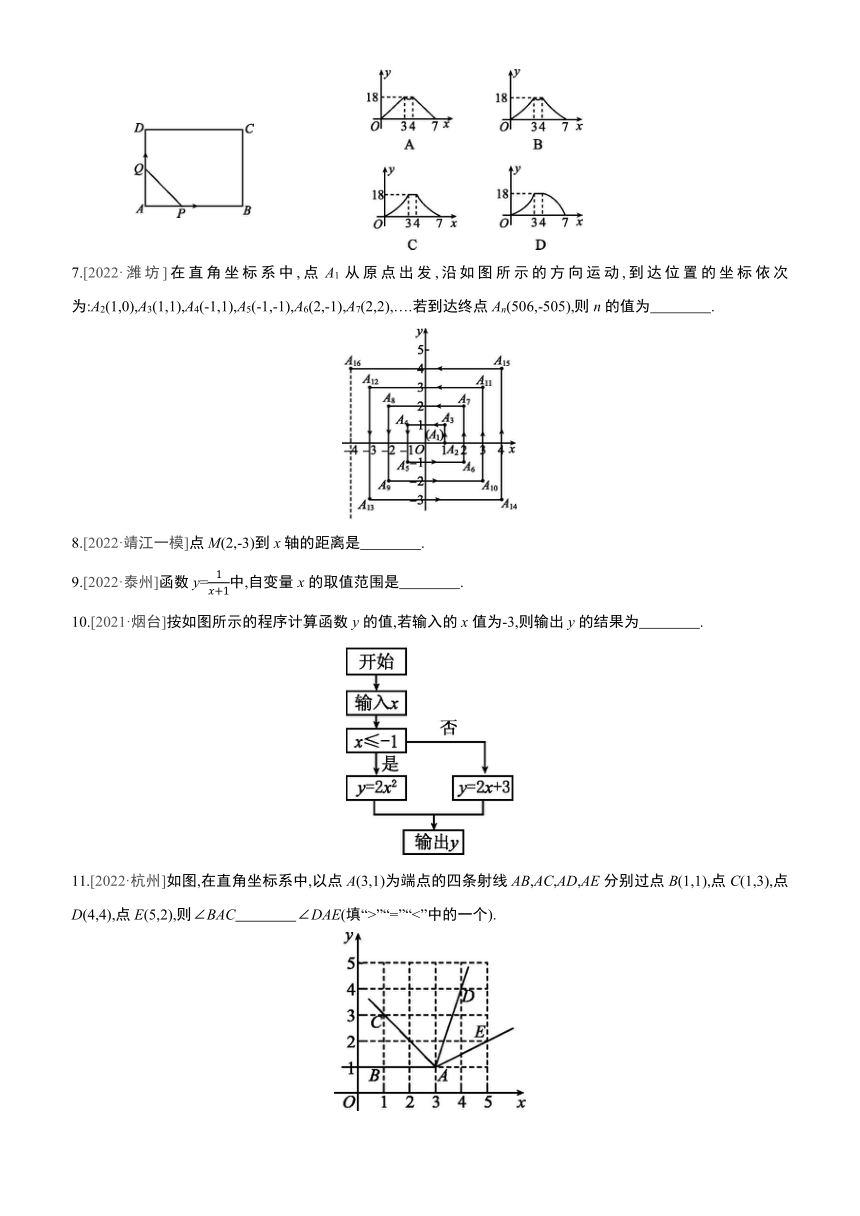
平面直角坐标系与函数
1.[2022·淮安模拟]若点A(1+m,1-n)与点B(-3,2)关于原点对称,则m+n的值为 ( )
A.-1 B.2 C.3 D.5
2.[2022·贵港]在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是 ( )
A.1 B.2 C.3 D.4
3.[2022·黄石]如图,△ABC的三个顶点都在方格纸的格点上,其中A点的坐标是(-1,0),现将△ABC绕A点按逆时针方向旋转90°,则旋转后点C的坐标是 ( )
A.(2,-3) B.(-2,3)
C.(-2,2) D.(-3,2)
4.[2022·常州]为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格y1(元/件)随时间t(天)的变化如图所示,设y2(元/件)表示从第1天到第t天该商品的平均价格,则y2随t变化的图像大致是图中的 ( )
5.[2022·雨花台区模拟]在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y-1,-x-1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2022的坐标为(-3,2),设A1(x,y),则x+y的值是 ( )
A.-5 B.3
C.-1 D.5
6.[2022·通辽]如图,在矩形ABCD中,AB=4,BC=3,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接PQ.设点P的运动路程为x,PQ2为y,则y关于x的函数图像大致是图中的 ( )
7.[2022·潍坊]在直角坐标系中,点A1从原点出发,沿如图所示的方向运动,到达位置的坐标依次为:A2(1,0),A3(1,1),A4(-1,1),A5(-1,-1),A6(2,-1),A7(2,2),….若到达终点An(506,-505),则n的值为 .
8.[2022·靖江一模]点M(2,-3)到x轴的距离是 .
9.[2022·泰州]函数y=中,自变量x的取值范围是 .
10.[2021·烟台]按如图所示的程序计算函数y的值,若输入的x值为-3,则输出y的结果为 .
11.[2022·杭州]如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2),则∠BAC ∠DAE(填“>”“=”“<”中的一个).
12.[2021·温州模拟]已知△ABC中,点A(-1,2),B(-3,-2),C(3,-3).在直角坐标系(图)中,画出△ABC,并求出△ABC的面积.
13.[2022·嘉兴]根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)y是关于x的函数吗 为什么
(2)“加速期”结束时,小斌的速度为多少
(3)根据图中提供的信息,给小斌提一条训练建议.
14.如图, △OAP 为等腰直角三角形,∠APO=90°, OP=AP,OA=4.
(1)如图①,点P的坐标为 ;
(2) 如图②,若点P在第二象限,且横坐标为-,则点A的坐标为 ;
(3)如图③,点H为x轴负半轴上一点,若∠AOH=60°,∠AHO=90°. 求点A,点P的坐标(用非特殊角的三角函数表示).
答案
1.D
2.C ∵点P(a-3,1)与点Q(2,b+1)关于x轴对称,
∴a-3=2,b+1=-1,
∴a=5,b=-2,
则a+b=5-2=3.故选C.
3.B
4.A 由商品的价格y1(元/件)随时间t(天)的变化图像得:商品的价格从5增长到15,然后保持15不变,一段时间后又下降到5,
∴第1天到第t天该商品的平均价格变化的规律是当1≤t≤6时,y2匀速增长;当65.C
6.C
7.2022
8.3
9.x≠-1
10.18
11.=
12.解:△ABC如图所示;△ABC的面积为13.
13.解:(1)y是关于x的函数,在这个变化过程中,对于x的每一个确定的值,y都有唯一确定的值与之对应.
(2)“加速期”结束时,小斌的速度为10.4 m/s.
(3)答案不唯一.例如:根据图像信息,小斌在80米左右时速度下降明显,建议增加耐力训练,提高成绩.
14.解:(1)(-2,2)
(2)(-,)
(3)∵∠AHO=90°,∠AOH=60°,AO=4,
∴OH=2,AH=2,
则A(-2,2).
过点P作PD⊥x轴于点D,则∠POD=180°-∠AOH-∠AOP=75°.
由△OAP为等腰直角三角形,AO=4可知,OP=2,在Rt△OPD中,OD=OP·cos∠POD,PD=OP·sin∠POD,
∴OD=2cos75°,PD=2sin75°,
∴点P坐标为(2cos75°,2sin75°)(或过点P向y轴作垂线段可得P(2sin15°,2cos15°)).
1.[2022·淮安模拟]若点A(1+m,1-n)与点B(-3,2)关于原点对称,则m+n的值为 ( )
A.-1 B.2 C.3 D.5
2.[2022·贵港]在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是 ( )
A.1 B.2 C.3 D.4
3.[2022·黄石]如图,△ABC的三个顶点都在方格纸的格点上,其中A点的坐标是(-1,0),现将△ABC绕A点按逆时针方向旋转90°,则旋转后点C的坐标是 ( )
A.(2,-3) B.(-2,3)
C.(-2,2) D.(-3,2)
4.[2022·常州]为规范市场秩序、保障民生工程,监管部门对某一商品的价格持续监控.该商品的价格y1(元/件)随时间t(天)的变化如图所示,设y2(元/件)表示从第1天到第t天该商品的平均价格,则y2随t变化的图像大致是图中的 ( )
5.[2022·雨花台区模拟]在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y-1,-x-1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,这样依次得到各点.若A2022的坐标为(-3,2),设A1(x,y),则x+y的值是 ( )
A.-5 B.3
C.-1 D.5
6.[2022·通辽]如图,在矩形ABCD中,AB=4,BC=3,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接PQ.设点P的运动路程为x,PQ2为y,则y关于x的函数图像大致是图中的 ( )
7.[2022·潍坊]在直角坐标系中,点A1从原点出发,沿如图所示的方向运动,到达位置的坐标依次为:A2(1,0),A3(1,1),A4(-1,1),A5(-1,-1),A6(2,-1),A7(2,2),….若到达终点An(506,-505),则n的值为 .
8.[2022·靖江一模]点M(2,-3)到x轴的距离是 .
9.[2022·泰州]函数y=中,自变量x的取值范围是 .
10.[2021·烟台]按如图所示的程序计算函数y的值,若输入的x值为-3,则输出y的结果为 .
11.[2022·杭州]如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2),则∠BAC ∠DAE(填“>”“=”“<”中的一个).
12.[2021·温州模拟]已知△ABC中,点A(-1,2),B(-3,-2),C(3,-3).在直角坐标系(图)中,画出△ABC,并求出△ABC的面积.
13.[2022·嘉兴]根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)y是关于x的函数吗 为什么
(2)“加速期”结束时,小斌的速度为多少
(3)根据图中提供的信息,给小斌提一条训练建议.
14.如图, △OAP 为等腰直角三角形,∠APO=90°, OP=AP,OA=4.
(1)如图①,点P的坐标为 ;
(2) 如图②,若点P在第二象限,且横坐标为-,则点A的坐标为 ;
(3)如图③,点H为x轴负半轴上一点,若∠AOH=60°,∠AHO=90°. 求点A,点P的坐标(用非特殊角的三角函数表示).
答案
1.D
2.C ∵点P(a-3,1)与点Q(2,b+1)关于x轴对称,
∴a-3=2,b+1=-1,
∴a=5,b=-2,
则a+b=5-2=3.故选C.
3.B
4.A 由商品的价格y1(元/件)随时间t(天)的变化图像得:商品的价格从5增长到15,然后保持15不变,一段时间后又下降到5,
∴第1天到第t天该商品的平均价格变化的规律是当1≤t≤6时,y2匀速增长;当6
6.C
7.2022
8.3
9.x≠-1
10.18
11.=
12.解:△ABC如图所示;△ABC的面积为13.
13.解:(1)y是关于x的函数,在这个变化过程中,对于x的每一个确定的值,y都有唯一确定的值与之对应.
(2)“加速期”结束时,小斌的速度为10.4 m/s.
(3)答案不唯一.例如:根据图像信息,小斌在80米左右时速度下降明显,建议增加耐力训练,提高成绩.
14.解:(1)(-2,2)
(2)(-,)
(3)∵∠AHO=90°,∠AOH=60°,AO=4,
∴OH=2,AH=2,
则A(-2,2).
过点P作PD⊥x轴于点D,则∠POD=180°-∠AOH-∠AOP=75°.
由△OAP为等腰直角三角形,AO=4可知,OP=2,在Rt△OPD中,OD=OP·cos∠POD,PD=OP·sin∠POD,
∴OD=2cos75°,PD=2sin75°,
∴点P坐标为(2cos75°,2sin75°)(或过点P向y轴作垂线段可得P(2sin15°,2cos15°)).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
