一元一次不等式与一次函数(1)[下学期]
文档属性
| 名称 | 一元一次不等式与一次函数(1)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-22 00:00:00 | ||
图片预览



文档简介
课件13张PPT。北 师 大? 八 年 级《 数 学 ( 下 ) 》1.5 一 元 一 次
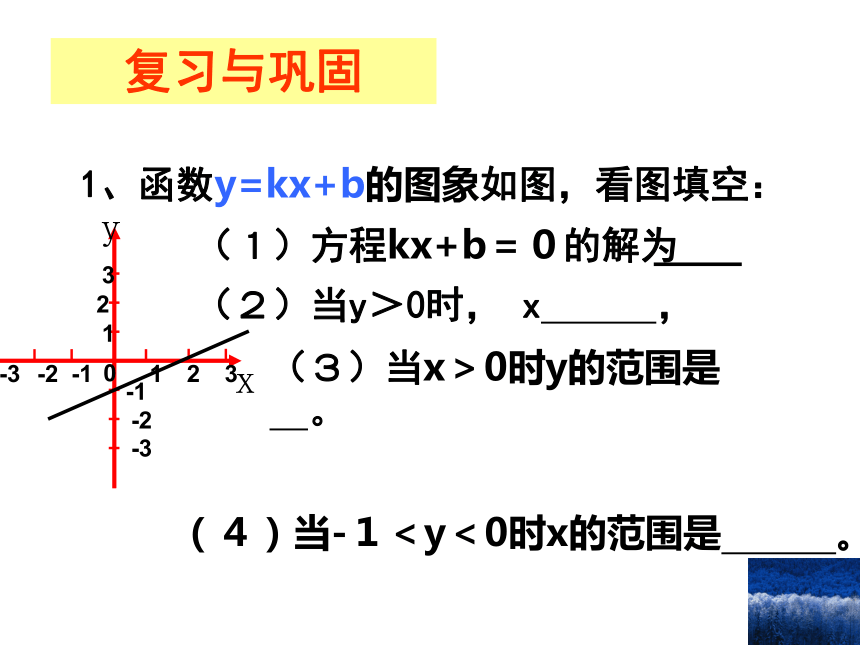
不 等 式 与一次函数(1)复习与巩固(4)当-1<y<0时x的范围是 。2、我们知道,一次函数的图象是一条直线。 作出一次函数 y = 2x - 5
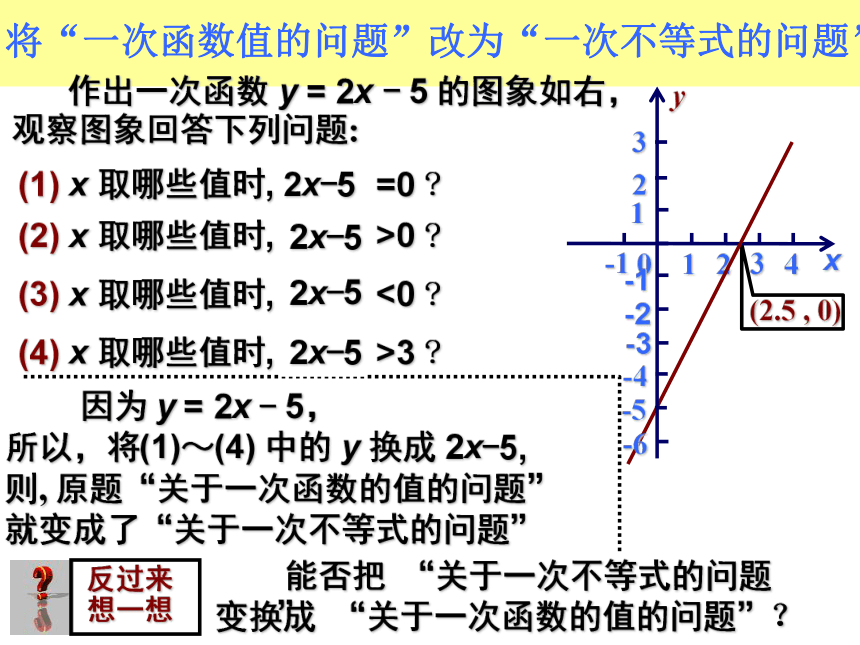
的图象如右,观察图象回答下列问题:(1) x 取哪些值时, y=0 ?(2) x 取哪些值时, y>0 ?x > 2.5 时 , y > 0 ;x = 2.5 时 , y = 0 ;(3) x 取哪些值时, y<0 ?x < 2.5 时 , y < 0 ;(4) x 取哪些值时, y>3 ?x > 4 时 , y > 3 ;将“一次函数值的问题”改为“一次不等式的问题” 作出一次函数 y = 2x - 5 的图象如右,观察图象回答下列问题:(1) x 取哪些值时, y =0 ?(2) x 取哪些值时, y >0 ?(3) x 取哪些值时, y <0 ?(4) x 取哪些值时, y >3 ?y所以,将(1)~(4) 中的 y 换成 2x-5,2x-52x-52x-52x-5则, 原题“关于一次函数的值的问题”就变成了“关于一次不等式的问题”变换成 “关于一次函数的值的问题”?由上述讨易知: 函数、(方程) 不等式“关于一次函数的值的问题”
可变换成 “关于一次不等式的问题” ; 反过来, “关于一次不等式的问题”
可变换成 “关于一次函数的值的问题”。 因此, 我们既可以运用函数图象解不等式 ,
也可以运用解不等式帮助研究函数问题 ,
二者相互渗透 ,互相作用。 不等式与 函数 、方程 是紧密联系着
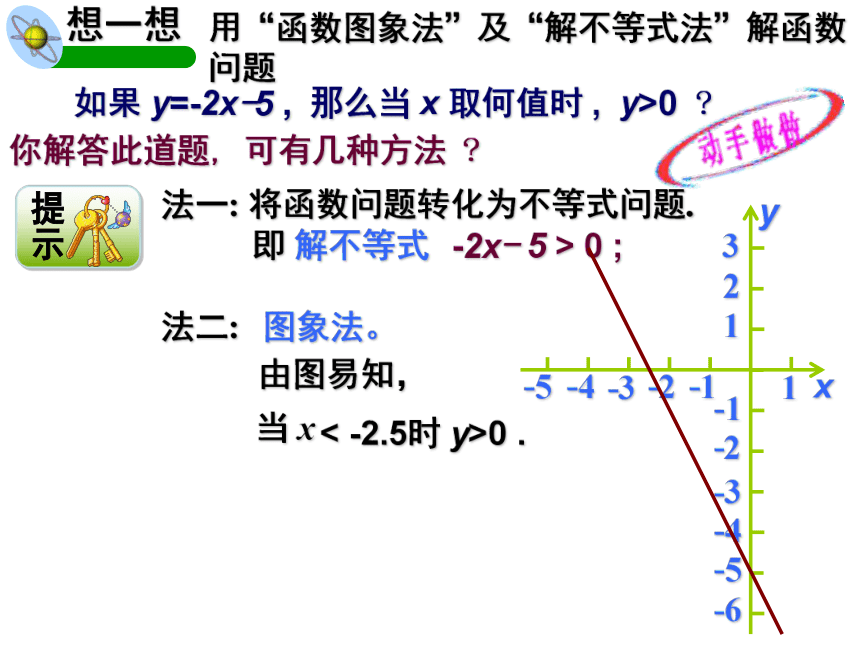
的一个整体 。 如果 y=-2x-5 , 那么当 x 取何值时 , y>0 ?你解答此道题, 可有几种方法 ? 将函数问题转化为不等式问题.即 解不等式-2x- 5 > 0 ;法二:图象法。< -2.5时 y>0 .用“函数图象法”及“解不等式法”解函数问题 兄弟俩赛跑,哥哥先让弟弟跑 9 米,然后自己才开始跑。
已知弟弟每秒跑 3 米,哥哥每秒跑 4 米。
列出函数关系式,画出函数图象,观察图象回答下列问题:做 一 做 (1) 何时弟弟跑在哥哥前面?用多种方法解行程问题P 20y1= ,y2= . (2) 何时哥哥跑在弟弟前面? (3) 谁先跑过 20米?谁先跑过 100米?你是怎样求的?与同伴交流。9+3x4xxy-20108642100908070605040302010(s)(m)yyyy哥哥弟弟(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。答案: (1) 从哥哥起跑开始 , 弟弟跑在哥哥前面;
(2) 从哥哥起跑开始 , 哥哥跑弟弟在前面;
(3) 先跑过 20米, 先跑过 100米 .9s 前9s 后弟弟哥哥2、先通过列方程找到追及弟弟的时间。 学以致用:
“创新课堂第10页----把握中考”
随堂练习:
已知y1=-x+3,y2=3x-4,试确定当x分别取何值时:
(1)y1 >y2 ?
(2)y1 =y2 ?
(3)y1 <y2 ?
你是怎样做的?与同伴交流。
一次函数(值)的变化对应着相应自变量的取值范围,
这个取值范围, 既可从一次函数的图象上直观看出(近似值),
也可通过解(方程)不等式而得到(精确值).“一次函数问题”可转换成 “一次不等式的问题” ;反过来,
“一次不等式的问题”可转换成 “一次函数的问题”。 我们既可以运用函数图象解不等式 ,
也可以运用解不等式帮助研究函数问题 ,
二者相互渗透 ,互相作用。
不等式与 函数 、方程 是紧密联系着
的一个整体 。 对于行程问题 , 应首先建立起“路程关于时间的函数关系式”,
再通过解不等式得到问题的解;
或先通过解方程求出追及(相遇)的时刻, 再解答相应的问题. 作 业习 题 1.61、2 ;P20一元一次不等式
与一次函数P19
不 等 式 与一次函数(1)复习与巩固(4)当-1<y<0时x的范围是 。2、我们知道,一次函数的图象是一条直线。 作出一次函数 y = 2x - 5
的图象如右,观察图象回答下列问题:(1) x 取哪些值时, y=0 ?(2) x 取哪些值时, y>0 ?x > 2.5 时 , y > 0 ;x = 2.5 时 , y = 0 ;(3) x 取哪些值时, y<0 ?x < 2.5 时 , y < 0 ;(4) x 取哪些值时, y>3 ?x > 4 时 , y > 3 ;将“一次函数值的问题”改为“一次不等式的问题” 作出一次函数 y = 2x - 5 的图象如右,观察图象回答下列问题:(1) x 取哪些值时, y =0 ?(2) x 取哪些值时, y >0 ?(3) x 取哪些值时, y <0 ?(4) x 取哪些值时, y >3 ?y所以,将(1)~(4) 中的 y 换成 2x-5,2x-52x-52x-52x-5则, 原题“关于一次函数的值的问题”就变成了“关于一次不等式的问题”变换成 “关于一次函数的值的问题”?由上述讨易知: 函数、(方程) 不等式“关于一次函数的值的问题”
可变换成 “关于一次不等式的问题” ; 反过来, “关于一次不等式的问题”
可变换成 “关于一次函数的值的问题”。 因此, 我们既可以运用函数图象解不等式 ,
也可以运用解不等式帮助研究函数问题 ,
二者相互渗透 ,互相作用。 不等式与 函数 、方程 是紧密联系着
的一个整体 。 如果 y=-2x-5 , 那么当 x 取何值时 , y>0 ?你解答此道题, 可有几种方法 ? 将函数问题转化为不等式问题.即 解不等式-2x- 5 > 0 ;法二:图象法。< -2.5时 y>0 .用“函数图象法”及“解不等式法”解函数问题 兄弟俩赛跑,哥哥先让弟弟跑 9 米,然后自己才开始跑。
已知弟弟每秒跑 3 米,哥哥每秒跑 4 米。
列出函数关系式,画出函数图象,观察图象回答下列问题:做 一 做 (1) 何时弟弟跑在哥哥前面?用多种方法解行程问题P 20y1= ,y2= . (2) 何时哥哥跑在弟弟前面? (3) 谁先跑过 20米?谁先跑过 100米?你是怎样求的?与同伴交流。9+3x4xxy-20108642100908070605040302010(s)(m)yyyy哥哥弟弟(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。答案: (1) 从哥哥起跑开始 , 弟弟跑在哥哥前面;
(2) 从哥哥起跑开始 , 哥哥跑弟弟在前面;
(3) 先跑过 20米, 先跑过 100米 .9s 前9s 后弟弟哥哥2、先通过列方程找到追及弟弟的时间。 学以致用:
“创新课堂第10页----把握中考”
随堂练习:
已知y1=-x+3,y2=3x-4,试确定当x分别取何值时:
(1)y1 >y2 ?
(2)y1 =y2 ?
(3)y1 <y2 ?
你是怎样做的?与同伴交流。
一次函数(值)的变化对应着相应自变量的取值范围,
这个取值范围, 既可从一次函数的图象上直观看出(近似值),
也可通过解(方程)不等式而得到(精确值).“一次函数问题”可转换成 “一次不等式的问题” ;反过来,
“一次不等式的问题”可转换成 “一次函数的问题”。 我们既可以运用函数图象解不等式 ,
也可以运用解不等式帮助研究函数问题 ,
二者相互渗透 ,互相作用。
不等式与 函数 、方程 是紧密联系着
的一个整体 。 对于行程问题 , 应首先建立起“路程关于时间的函数关系式”,
再通过解不等式得到问题的解;
或先通过解方程求出追及(相遇)的时刻, 再解答相应的问题. 作 业习 题 1.61、2 ;P20一元一次不等式
与一次函数P19
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
