2023年中考数学(苏科版)总复习二轮专题突破课件: 02 函数实际应用型问题(共64张PPT)
文档属性
| 名称 | 2023年中考数学(苏科版)总复习二轮专题突破课件: 02 函数实际应用型问题(共64张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 10:56:18 | ||
图片预览





文档简介
(共64张PPT)
●教材梳理 夯实基础
专题突破(二)
函数实际应用型问题
函数实际应用型问题是把题中数量关系抽象为函数模型,如一次函数、二次函数、反比例函数以及由它们组合的分段函数,进而应用函数进行分析、研究、解决有关问题.函数的实质是研究两变量之间的对应关系,用函数思想构建数学模型解决实际问题.
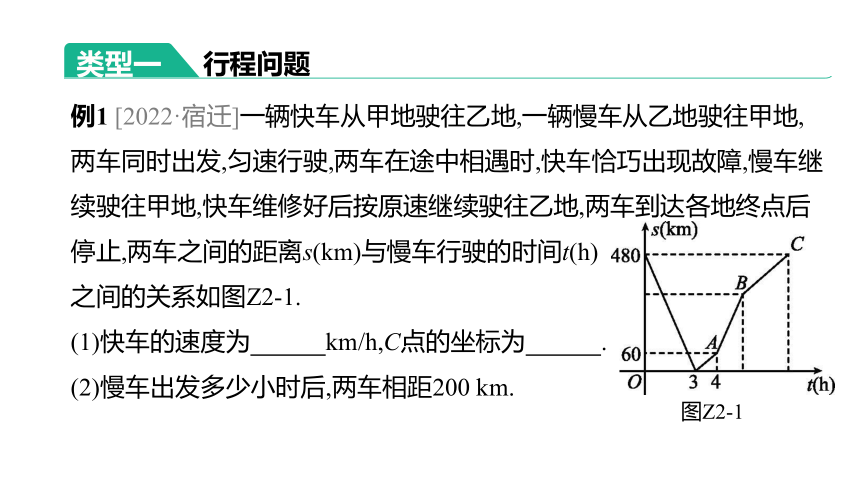
例1 [2022·宿迁]一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续驶往乙地,两车到达各地终点后停止,两车之间的距离s(km)与慢车行驶的时间t(h)
之间的关系如图Z2-1.
(1)快车的速度为 km/h,C点的坐标为 .
(2)慢车出发多少小时后,两车相距200 km.
类型一
行程问题
图Z2-1
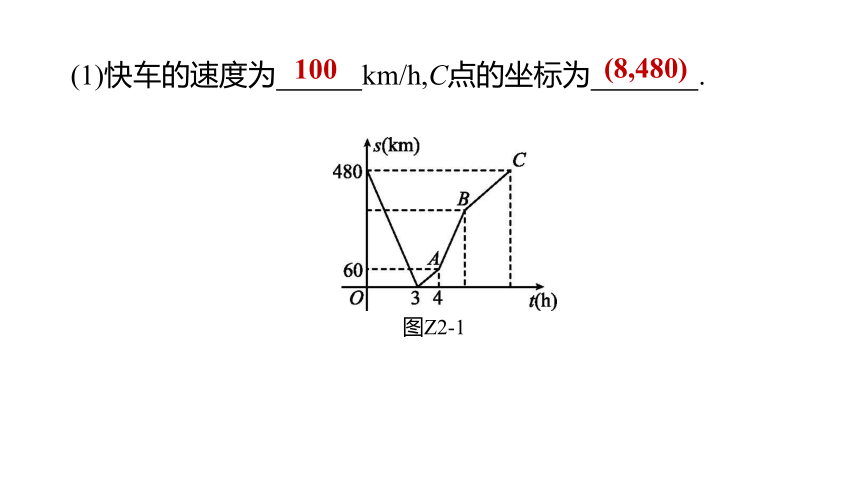
(1)快车的速度为 km/h,C点的坐标为 .
图Z2-1
100
(8,480)
[解析]由图像可知:慢车的速度为60÷(4-3)=60(km/h).
∵两车3小时相遇,此时慢车走的路程为:60×3=180(km),
∴快车的速度为:(480-180)÷3=300÷3=100(km/h),
通过图像和甲、乙两车速度可知快车比慢车先到达终点,
∴慢车到达终点时所用时间为
480÷60=8(h),∴C点坐标为(8,480),
故答案为100,(8,480).
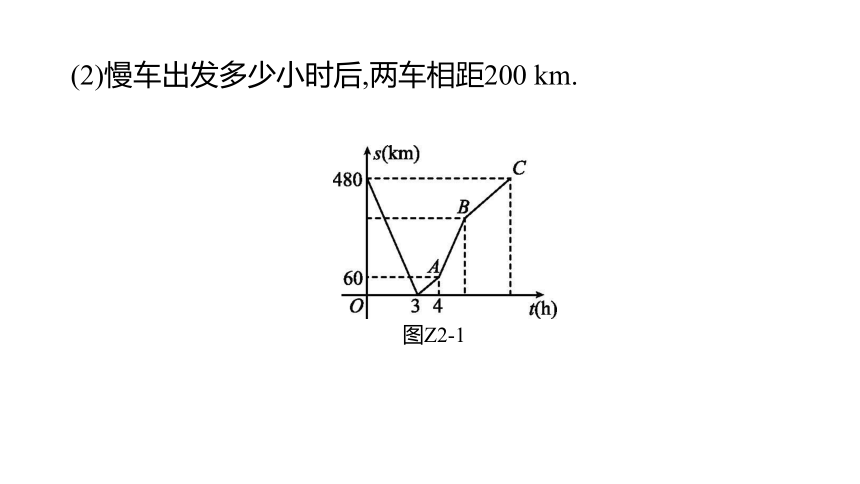
(2)慢车出发多少小时后,两车相距200 km.
图Z2-1
解:(2)方法一:设慢车出发t小时后两车相距200 km,
①相遇前两车相距200 km,则:60t+100t+200=480,
解得:t=.
②相遇后两车相距200 km,则:60t+100(t-1)-480=200,
解得:t=,
∴慢车出发h或h时两车相距200 km.
方法二:①当两车相遇前(0≤t≤3),
设s=k1t+b1,把(0,480),(3,0)代入,得s=-160t+480,
令-160t+480=200.解得:t=.
②由B点表示的实际意义,可得B(5.8,348),
两车相遇后,由图可知4≤t≤5.8时,存在相距200 km.
设s=k2t+b2,把(4,60),(5.8,348)代入,得s=160t-580,
令160t-580=200,解得t=.
综上所述:慢车出发 h或 h时,两车相距200 km.
|题型精练|
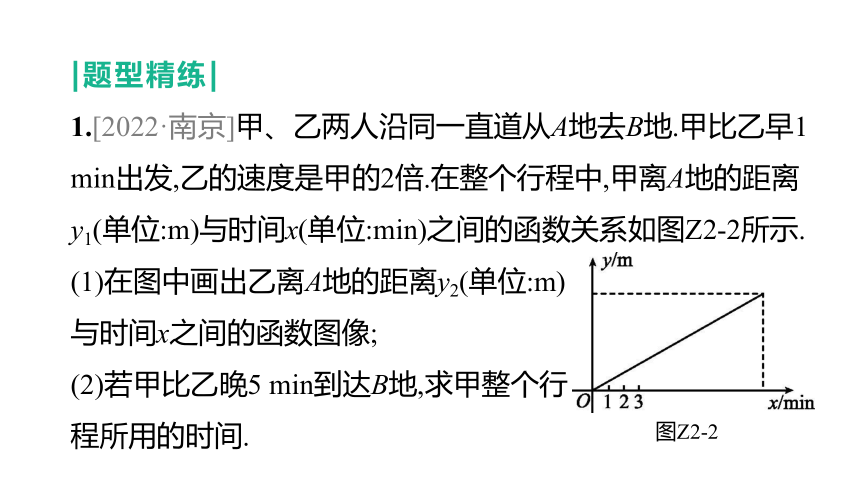
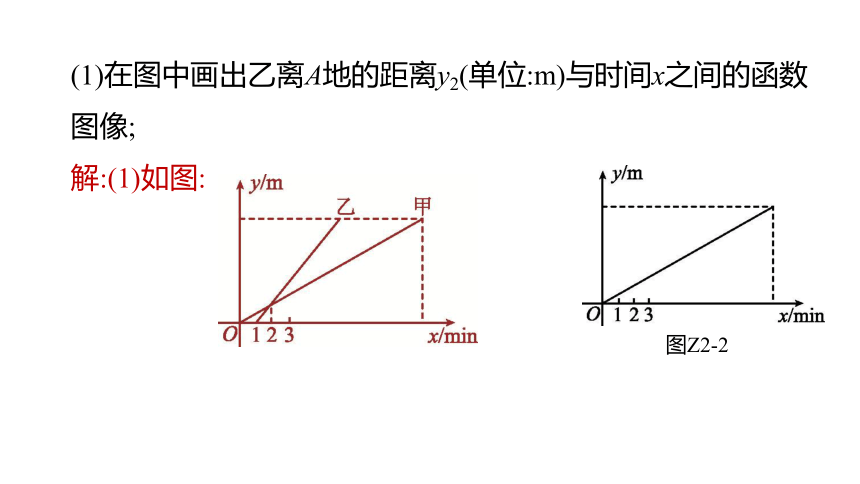
1.[2022·南京]甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离y1(单位:m)与时间x(单位:min)之间的函数关系如图Z2-2所示.
(1)在图中画出乙离A地的距离y2(单位:m)
与时间x之间的函数图像;
(2)若甲比乙晚5 min到达B地,求甲整个行
程所用的时间.
图Z2-2
(1)在图中画出乙离A地的距离y2(单位:m)与时间x之间的函数图像;
解:(1)如图:
图Z2-2
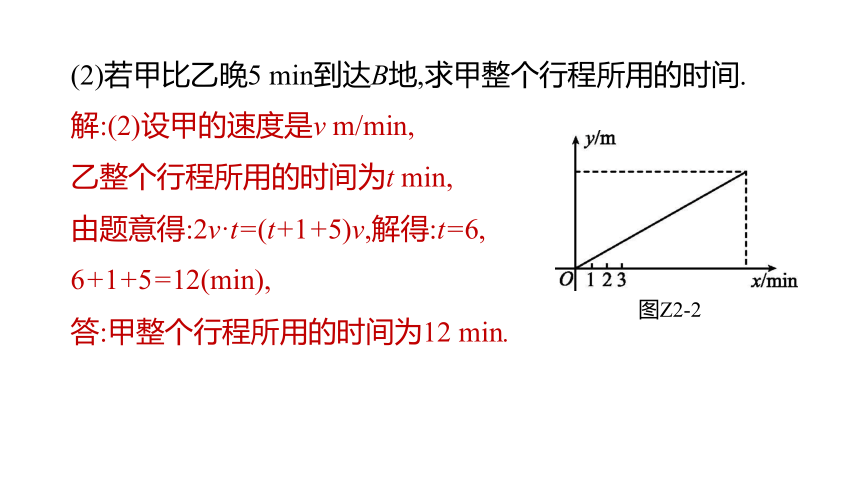
(2)若甲比乙晚5 min到达B地,求甲整个行程所用的时间.
图Z2-2
解:(2)设甲的速度是v m/min,
乙整个行程所用的时间为t min,
由题意得:2v·t=(t+1+5)v,解得:t=6,
6+1+5=12(min),
答:甲整个行程所用的时间为12 min.
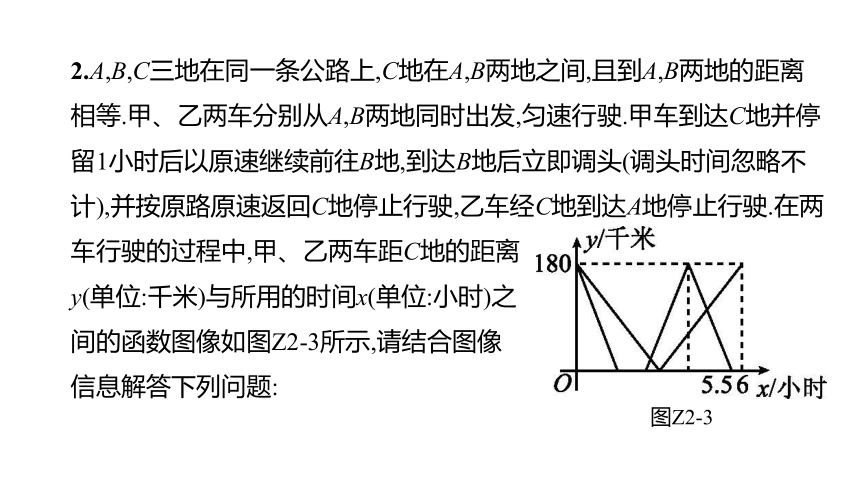
2.A,B,C三地在同一条公路上,C地在A,B两地之间,且到A,B两地的距离相等.甲、乙两车分别从A,B两地同时出发,匀速行驶.甲车到达C地并停留1小时后以原速继续前往B地,到达B地后立即调头(调头时间忽略不计),并按原路原速返回C地停止行驶,乙车经C地到达A地停止行驶.在两车行驶的过程中,甲、乙两车距C地的距离
y(单位:千米)与所用的时间x(单位:小时)之
间的函数图像如图Z2-3所示,请结合图像
信息解答下列问题:
图Z2-3
(1)直接写出A,B两地的距离和甲车的速度.
(2)求乙车从C地到A地的过程中y与x的函数关系式(不用写自变量的取值范围).
(3)出发后几小时,两车在途中距C地的距离之和为180千米 请直接写出答案.
(1)直接写出A,B两地的距离和甲车的速度.
图Z2-3
解:(1)当x=0时,甲车和乙车距C地均为
180千米,
∴A,B两地的距离为180+180=360(千米).
设甲车经过180千米用了x小时,
则:x+x+x+1=5.5,∴x=1.5,
则甲车速度为:180÷1.5=120(千米/时).
(2)求乙车从C地到A地的过程中y与x的函数关系式(不用写自变量的取值范围).
图Z2-3
解:(2)设乙车从C地到A地的过程中y与
x的函数关系式为:y=kx+b(k≠0),
将(3,0),(6,180)代入y=kx+b(k≠0),
得解得
∴乙车从C地到A地的过程中y与x的函数关系式为:y=60x-180.
(3)出发后几小时,两车在途中距C地的距离之和为180千米 请直接写出答案.
图Z2-3
解:(3)出发后1小时,小时,5小时时,
两车在途中距C地的距离之和为180
千米.
[解析] 由图可知,分别在3个时间段讨论两车在途中距C地距离之和为180千米.
①甲车从A地到C地,乙车从B地到C地,-120x+180-60x+180=180,解得x=1.
②甲车从C地到B地,乙车从C地到A地,120x-300+60x-180=180,解得x=.
③甲车从B地到C地,乙车从C地到A地,
-120x+660+60x-180=180,解得x=5.
综上所述:分别在1小时,小时,5小时这三个
时间点,两车在途中距C地的距离之和为180千米.
3.[2022·徐州]如图Z2-4①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点A.甲从中山路上点B出发,骑车向北匀速直行;与此同时,乙从点A出发,沿北京路步行向东匀速直行.设出发x min时,甲、
乙两人与点A的距离分别为y1 m,y2 m.已知y1,y2与x之间的函数关系如图②所示.
(1)求甲、乙两人的速度.
(2)当x取何值时,甲、乙两人之间
的距离最短
① ②
图Z2-4
(1)求甲、乙两人的速度.
① ②
图Z2-4
解:(1)设甲的速度为a m/min,乙的速
度为b m/min,
根据题意有:
解得
∴甲的速度是240 m/min,乙的速度是80 m/min.
解:(2)甲、乙两人之间的距离
=
=80,
当x=-=4.5(min)时,甲、
乙两人之间的距离最短.
(2)当x取何值时,甲、乙两人之间的距离最短
① ②
图Z2-4
例2 [2022·宜昌]甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元/ kg,如果一次购买4 kg以上的苹果,超过4 kg的部分按标价6折售卖.
x(单位: kg)表示购买苹果的质量,y(单位:元)表示付款金额.
类型二
阶梯收费问题
(1)文文购买3 kg苹果需付款 元;购买5 kg苹果需付款
元.
(2)求付款金额y关于购买苹果的质量x的函数解析式.
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/ kg,且全部按标价的8折售卖,文文如果要购买10 kg苹果,请问她在哪个超市购买更划算.
(1)文文购买3 kg苹果需付款 元;购买5 kg苹果需付款
元.
30
46
[解析]由题意可知:文文购买3 kg苹果不优惠,∴文文购买3 kg苹果需付款:3×10=30(元),购买5 kg苹果,4 kg不优惠,1 kg优惠,
∴购买5 kg苹果需付款:4×10+1×10×0.6=46(元),
故答案为:30,46.
(2)求付款金额y关于购买苹果的质量x的函数解析式.
解:(2)由题意得,当0当x>4时,y=4×10+(x-4)×10×0.6=6x+16,
∴付款金额y关于购买苹果的质量x的函数解析式为:
y=
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/ kg,且全部按标价的8折售卖,文文如果要购买10 kg苹果,请问她在哪个超市购买更划算.
解:文文在甲超市购买10 kg苹果需付款:6×10+16=76(元),
文文在乙超市购买10 kg苹果需付款:10×10×0.8=80(元),
∵76<80,∴文文在甲超市购买更划算.
|题型精练|
为解决消费者停车难的问题,某商场新建一小型轿车停车场,经测算,此停车场每天需固定支出的费用(包括设施维修费、管理人员工资等)为600元,为制定合理的收费标准,该商场对每天轿车停放辆次(每辆轿车每停放一次简称为“辆次”)与每辆轿车的收费情况进行调查,发现每辆次轿车的停车费定价不超过10元时,每天来此停放的轿车都为300辆次.若每辆次轿车的停车费定价超过10元,则每超过1元,每天来此停放的轿车就减少12辆次,设每辆次轿车的停车费为x元(为便于结算,停车费x只取整数),此停车场的日净收入为y元(日净收入=每天共收停车费-每天固定的支出),回答下列问题:
(1)①当x≤10时,y与x的关系式为: .
②当x>10时,y与x的关系式为: .
(2)停车场能否实现3000元的日净收入 如能实现,求出每辆次轿车的停车费定价,如不能实现,请说明理由.
(3)该商场要求此停车场既要吸引顾客,使每天轿车停放的辆次较多,又要有最大的日净收入,按此要求,每辆次轿车的停车费定价应定为多少元 此时最大日净收入是多少元
(1)①当x≤10时,y与x的关系式为: .
②当x>10时,y与x的关系式为:__________________________
.
y=300x-600
y=[300-12(x-10)]x-600,即
y=-12x2+420x-600.
(2)停车场能否实现3000元的日净收入 如能实现,求出每辆次轿车的停车费定价,如不能实现,请说明理由.
解:(2)依题意有:①当x≤10时,300x-600=3000,
解得x=12,不符合题意;
②x>10时,-12x2+420x-600=3000,
解得x1=15,x2=20.
故停车场能实现3000元的日净收入,每辆次轿车的停车费定价是15元或20元.
(3)该商场要求此停车场既要吸引顾客,使每天轿车停放的辆次较多,又要有最大的日净收入,按此要求,每辆次轿车的停车费定价应定为多少元 此时最大日净收入是多少元
解:(3)当x≤10时,停车300辆次,最大日净收入
y=300×10-600=2400(元).
当x>10时,y=-12x2+420x-600=-12(x-17.5)2+3075,
∴当x=17.5时,y有最大值,但x只能取整数,∴x取17或18.
显然,x取17或18时,此时最大日净收入为
y=-12×0.25+3075=3072(元).
∵需要轿车停放辆次较多,∴每辆次轿车的停车费定价应定为17元,此时最大日净收入是3072元.
例3 某学校小组利用暑假中前40天参加社会实践活动,参与了一家网上书店经营,了解到一种成本为每本20元的书在x天销售量P=50-x.在第x天的售价为每本y元,y与x的关系如图Z2-5所示.已知当社会实践活动
时间超过一半后,y=20+.
(1)请求出当1≤x≤20时,y与x的函数关系式,
并求出第12天此书的销售单价;
(2)这40天中该网点销售此书第几天获得的
利润最大 最大利润是多少
类型三
最大利润问题
图Z2-5
(1)请求出当1≤x≤20时,y与x的函数关系式,并求出第12天此书的销售单价;
图Z2-5
解:(1)当1≤x≤20时,设y=kx+b,将(1,30.5),
(20,40)代入,得解得
则y与x的函数关系式为:y=x+30(1≤x≤20),
当x=12时,y=6+30=36.
∴第12天此书的销售单价为36元.
(2)这40天中该网点销售此书第几天获得的利润最大 最大利润是多少
图Z2-5
解:(2)设该网店第x天获得的利润为w元.
当1≤x≤20时,w=(x+30-20)(50-x)=-x2+15x+500
=-(x-15)2+,∵-<0,∴当x=15时,w有最大值w1,且w1=612.5.
当21≤x≤40时,w=(20+-20)(50-x)=-315.
∵15750>0,∴随x的增大而减小,∴x=21时,最大.
于是,x=21时,w有最大值w2,且w2=-315=435.∵w1>w2,
∴这40天中该网点销售此书第15天获得的利润最大,最大利润是612.5元.
|题型精练|
1.[2022·连云港]某快餐店销售A,B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是
元.
1264
[解析]设每份A种快餐降价a元,则每天卖出(40+2a)份,每份B种快餐提高b元,则每天卖出(80-2b)份.
由题意,得40+2a+80-2b=40+80,解得a=b,
∴总利润W=(12-a)(40+2a)+(8+a)(80-2a)=-4a2+48a+1120
=-4(a-6)2+1264.
∵-4<0,∴当a=6时,W取得最大值1264,
即两种快餐一天的总利润最多为1264元.
2.[2022·聊城]为迎接建党一百周年,我市计划用两种花卉对某广场进行美化.已知用600元购买A种花卉与用900元购买B种花卉的数量相等,且B种花卉每盆比A种花卉多0.5元.
(1)A,B两种花卉每盆各多少元
(2)计划购买A,B两种花卉共6000盆,其中A种花卉的数量不超过B种花卉数量的,求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元.
(1)A,B两种花卉每盆各多少元
解:(1)设A种花卉每盆x元,则B种花卉每盆(x+0.5)元.
根据题意,得=.
解这个方程,得x=1.
经检验知,x=1是原分式方程的根,且符合题意.此时x+0.5=1.5(元).
所以,A种花卉每盆1元,B种花卉每盆1.5元.
(2)计划购买A,B两种花卉共6000盆,其中A种花卉的数量不超过B种花卉数量的,求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元.
解:(2)设购买A种花卉t盆,则购买B种花卉(6000-t)盆,设购买这批花卉的总费用为w元,则t≤(6000-t),解得t≤1500.
由题意,得w=t+1.5(6000-t)=-0.5t+9000.
因为w是t的一次函数,k=-0.5<0,所以w随t的增大而减小,
所以当t=1500时,w最小.w最小=-0.5×1500+9000=8250(元).
所以,购买A种花卉1500盆时购买这批花卉总费用最低,最低费用为8250元.
3.[2022·大连]某电商销售某种商品一段时间后,发现该商品每天的销售量y(单位:千克)和每千克的售价x(单位:元)满足一次函数关系(如图Z2-6所示),其中50≤x≤80.
(1)求y关于x的函数解析式;
(2)若该种商品的成本为每千克40元,该电
商如何定价才能使每天获得的利润最大
最大利润是多少
图Z2-6
(1)求y关于x的函数解析式;
图Z2-6
解:(1)设y=kx+b,将(50,100)、(80,40)代入,
得解得
∴y关于x的函数解析式为
y=-2x+200(50≤x≤80).
(2)若该种商品的成本为每千克40元,该电商如何定价才能使每天获得的利润最大 最大利润是多少
图Z2-6
解:(2)设电商每天获得的利润为w元,
则w=(x-40)(-2x+200)=-2x2+280x-8000=-2(x-70)2+1800.
∵-2<0,且对称轴是直线x=70,50≤x≤80,
∴当x=70时,w取得最大值,最大值为1800.
答:该电商定价该商品的售价为每千克70元时每天获得的利润最大,最大利润是1800元.
例4 [2022·河南]暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下:
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用
按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用
为y1(元),且y1=k1x+b;按照方案二所需费用为
y2(元),且y2=k2x.其函数图像如图Z2-7所示.
类型四
方案设计问题
图Z2-7
(1)求k1和b的值,并说明它们的实际意义.
(2)求打折前的每次健身费用和k2的值.
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少 说明理由.
(1)求k1和b的值,并说明它们的实际意义.
图Z2-7
解:(1)∵直线y1=k1x+b经过(0,30)和(10,180)
两点,
∴解得:
k1表示每次健身费用按六折优惠后的费用为
15元,b表示暑期专享卡每张30元.
(2)求打折前的每次健身费用和k2的值.
解(2)∵每次健身费用按六折优惠后的费用
为15元,
∴打折前的每次健身费用为15÷0.6=25(元).
∵不购买学生暑期专享卡,每次健身费用按
八折优惠,
∴k2=25×0.8=20.
图Z2-7
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少 说明理由.
解:(3)当x=8时,y1=15x+30=15×8+30=150,
y2=20x=20×8=160,
∵150<160,
∴选择方案一所需费用更少.
图Z2-7
|题型精练|
[2022·连云港]为了做好防疫工作,学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.
(1)这两种消毒液的单价各是多少元
(2)学校准备购进这两种消毒液共90瓶,且B型消毒液的数量不
少于A型消毒液数量的,请设计出最省钱的购买方案,并求出
最少费用.
(1)这两种消毒液的单价各是多少元
解:(1)设A型消毒液的单价是x元,B型消毒液的单价是y元,
由题意得 解得
答:A型消毒液的单价是7元,B型消毒液的单价是9元.
(2)学校准备购进这两种消毒液共90瓶,且B型消毒液的数量不
少于A型消毒液数量的,请设计出最省钱的购买方案,并求出
最少费用.
解:(2)设购进A型消毒液a瓶,费用为w元,则购进B型消毒液(90-a)瓶,依题意可得:w=7a+9(90-a)=-2a+810,
∴w随a的增大而减小.
∵B型消毒液的数量不少于A型消毒液数量的,
∴90-a≥a,解得a≤67.5,∴当x=67时,w取得最小值,此时,
w=-2×67+810=676,90-a=23,
答:最省钱的购买方案是购进A型消毒液67瓶,购进B型消毒液23瓶,最低费用为676元.
例5 [2022·无锡]有一块矩形地块ABCD,AB=20米,BC=30米.为美观,拟种植不同的花卉,如图Z2-8所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种
植乙种花卉;在矩形EFGH中种植丙种花卉.甲、
乙、丙三种花卉的种植成本分别为20元/米2、60
元/米2、40元/米2,设三种花卉的种植总成本为y元.
类型五
几何面积问题
图Z2-8
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120米2,求三种花卉的最低种植总成本.
(1)当x=5时,求种植总成本y;
图Z2-8
解:(1)当x=5时,EF=20-2x=10,
EH=30-2x=20,
y=2×(EH+AD)×x×20+2×(GH+CD)×
x×60+EF·EH×40
=(20+30)×5×20+(10+20)×5×60+20×10×40=22000.
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
图Z2-8
解:(2)EF=20-2x,EH=30-2x,
由题意得:y=2×(30+30-2x)·x·20+
2×(20+20-2x)·x·60+(30-2x)(20-2x)·40
=-400x+24000(0(3)若甲、乙两种花卉的种植面积之差不超过120米2,求三种花卉的最低种植总成本.
图Z2-8
解:(3)甲种花卉的种植面积
S甲=2×(EH+AD)×x=(30-2x+30)x=-2x2+60x,
同理乙种花卉的种植面积S乙=-2x2+40x,
∵甲、乙两种花卉的种植面积之差不超过120米2,
∴-2x2+60x-(-2x2+40x)≤120,解得:x≤6,故0而y=-400x+24000中y随x的增大而减小,
故当x=6时,y的最小值为21600,
即三种花卉的最低种植总成本为21600元.
|题型精练|
[2022·沭阳模拟]如图Z2-9,在Rt△ABC中,∠A=90°,AB=8 cm,AC=6 cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B,A重合的情况),运动速度为2 cm/s,过点D作DE∥BC交AC于点E,连接BE,设动点D运动的时间为x(s),AE的长为y(cm).
(1)求y关于x的函数表达式,并写出自变量x
的取值范围.
(2)当x为何值时,△BDE的面积S有最大值
最大值为多少
图Z2-9
(1)求y关于x的函数表达式,并写出自变量x的取值范围.
图Z2-9
解:(1)动点D运动x s后,BD=2x.
∵AB=8,∴AD=8-2x.
∵DE∥BC,∴=,
∴AE==6-x,
∴y关于x的函数表达式为y=-x+6(0(2)当x为何值时,△BDE的面积S有最大值 最大值为多少
图Z2-9
解:(2)S=·BD·AE
=×2x(-x+6)=-x2+6x
=-(x-2)2+6(0∴当x=2时,△BDE的面积S有最大值,最大值为6 cm2.
●教材梳理 夯实基础
专题突破(二)
函数实际应用型问题
函数实际应用型问题是把题中数量关系抽象为函数模型,如一次函数、二次函数、反比例函数以及由它们组合的分段函数,进而应用函数进行分析、研究、解决有关问题.函数的实质是研究两变量之间的对应关系,用函数思想构建数学模型解决实际问题.
例1 [2022·宿迁]一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续驶往乙地,两车到达各地终点后停止,两车之间的距离s(km)与慢车行驶的时间t(h)
之间的关系如图Z2-1.
(1)快车的速度为 km/h,C点的坐标为 .
(2)慢车出发多少小时后,两车相距200 km.
类型一
行程问题
图Z2-1
(1)快车的速度为 km/h,C点的坐标为 .
图Z2-1
100
(8,480)
[解析]由图像可知:慢车的速度为60÷(4-3)=60(km/h).
∵两车3小时相遇,此时慢车走的路程为:60×3=180(km),
∴快车的速度为:(480-180)÷3=300÷3=100(km/h),
通过图像和甲、乙两车速度可知快车比慢车先到达终点,
∴慢车到达终点时所用时间为
480÷60=8(h),∴C点坐标为(8,480),
故答案为100,(8,480).
(2)慢车出发多少小时后,两车相距200 km.
图Z2-1
解:(2)方法一:设慢车出发t小时后两车相距200 km,
①相遇前两车相距200 km,则:60t+100t+200=480,
解得:t=.
②相遇后两车相距200 km,则:60t+100(t-1)-480=200,
解得:t=,
∴慢车出发h或h时两车相距200 km.
方法二:①当两车相遇前(0≤t≤3),
设s=k1t+b1,把(0,480),(3,0)代入,得s=-160t+480,
令-160t+480=200.解得:t=.
②由B点表示的实际意义,可得B(5.8,348),
两车相遇后,由图可知4≤t≤5.8时,存在相距200 km.
设s=k2t+b2,把(4,60),(5.8,348)代入,得s=160t-580,
令160t-580=200,解得t=.
综上所述:慢车出发 h或 h时,两车相距200 km.
|题型精练|
1.[2022·南京]甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离y1(单位:m)与时间x(单位:min)之间的函数关系如图Z2-2所示.
(1)在图中画出乙离A地的距离y2(单位:m)
与时间x之间的函数图像;
(2)若甲比乙晚5 min到达B地,求甲整个行
程所用的时间.
图Z2-2
(1)在图中画出乙离A地的距离y2(单位:m)与时间x之间的函数图像;
解:(1)如图:
图Z2-2
(2)若甲比乙晚5 min到达B地,求甲整个行程所用的时间.
图Z2-2
解:(2)设甲的速度是v m/min,
乙整个行程所用的时间为t min,
由题意得:2v·t=(t+1+5)v,解得:t=6,
6+1+5=12(min),
答:甲整个行程所用的时间为12 min.
2.A,B,C三地在同一条公路上,C地在A,B两地之间,且到A,B两地的距离相等.甲、乙两车分别从A,B两地同时出发,匀速行驶.甲车到达C地并停留1小时后以原速继续前往B地,到达B地后立即调头(调头时间忽略不计),并按原路原速返回C地停止行驶,乙车经C地到达A地停止行驶.在两车行驶的过程中,甲、乙两车距C地的距离
y(单位:千米)与所用的时间x(单位:小时)之
间的函数图像如图Z2-3所示,请结合图像
信息解答下列问题:
图Z2-3
(1)直接写出A,B两地的距离和甲车的速度.
(2)求乙车从C地到A地的过程中y与x的函数关系式(不用写自变量的取值范围).
(3)出发后几小时,两车在途中距C地的距离之和为180千米 请直接写出答案.
(1)直接写出A,B两地的距离和甲车的速度.
图Z2-3
解:(1)当x=0时,甲车和乙车距C地均为
180千米,
∴A,B两地的距离为180+180=360(千米).
设甲车经过180千米用了x小时,
则:x+x+x+1=5.5,∴x=1.5,
则甲车速度为:180÷1.5=120(千米/时).
(2)求乙车从C地到A地的过程中y与x的函数关系式(不用写自变量的取值范围).
图Z2-3
解:(2)设乙车从C地到A地的过程中y与
x的函数关系式为:y=kx+b(k≠0),
将(3,0),(6,180)代入y=kx+b(k≠0),
得解得
∴乙车从C地到A地的过程中y与x的函数关系式为:y=60x-180.
(3)出发后几小时,两车在途中距C地的距离之和为180千米 请直接写出答案.
图Z2-3
解:(3)出发后1小时,小时,5小时时,
两车在途中距C地的距离之和为180
千米.
[解析] 由图可知,分别在3个时间段讨论两车在途中距C地距离之和为180千米.
①甲车从A地到C地,乙车从B地到C地,-120x+180-60x+180=180,解得x=1.
②甲车从C地到B地,乙车从C地到A地,120x-300+60x-180=180,解得x=.
③甲车从B地到C地,乙车从C地到A地,
-120x+660+60x-180=180,解得x=5.
综上所述:分别在1小时,小时,5小时这三个
时间点,两车在途中距C地的距离之和为180千米.
3.[2022·徐州]如图Z2-4①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点A.甲从中山路上点B出发,骑车向北匀速直行;与此同时,乙从点A出发,沿北京路步行向东匀速直行.设出发x min时,甲、
乙两人与点A的距离分别为y1 m,y2 m.已知y1,y2与x之间的函数关系如图②所示.
(1)求甲、乙两人的速度.
(2)当x取何值时,甲、乙两人之间
的距离最短
① ②
图Z2-4
(1)求甲、乙两人的速度.
① ②
图Z2-4
解:(1)设甲的速度为a m/min,乙的速
度为b m/min,
根据题意有:
解得
∴甲的速度是240 m/min,乙的速度是80 m/min.
解:(2)甲、乙两人之间的距离
=
=80,
当x=-=4.5(min)时,甲、
乙两人之间的距离最短.
(2)当x取何值时,甲、乙两人之间的距离最短
① ②
图Z2-4
例2 [2022·宜昌]甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元/ kg,如果一次购买4 kg以上的苹果,超过4 kg的部分按标价6折售卖.
x(单位: kg)表示购买苹果的质量,y(单位:元)表示付款金额.
类型二
阶梯收费问题
(1)文文购买3 kg苹果需付款 元;购买5 kg苹果需付款
元.
(2)求付款金额y关于购买苹果的质量x的函数解析式.
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/ kg,且全部按标价的8折售卖,文文如果要购买10 kg苹果,请问她在哪个超市购买更划算.
(1)文文购买3 kg苹果需付款 元;购买5 kg苹果需付款
元.
30
46
[解析]由题意可知:文文购买3 kg苹果不优惠,∴文文购买3 kg苹果需付款:3×10=30(元),购买5 kg苹果,4 kg不优惠,1 kg优惠,
∴购买5 kg苹果需付款:4×10+1×10×0.6=46(元),
故答案为:30,46.
(2)求付款金额y关于购买苹果的质量x的函数解析式.
解:(2)由题意得,当0
∴付款金额y关于购买苹果的质量x的函数解析式为:
y=
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/ kg,且全部按标价的8折售卖,文文如果要购买10 kg苹果,请问她在哪个超市购买更划算.
解:文文在甲超市购买10 kg苹果需付款:6×10+16=76(元),
文文在乙超市购买10 kg苹果需付款:10×10×0.8=80(元),
∵76<80,∴文文在甲超市购买更划算.
|题型精练|
为解决消费者停车难的问题,某商场新建一小型轿车停车场,经测算,此停车场每天需固定支出的费用(包括设施维修费、管理人员工资等)为600元,为制定合理的收费标准,该商场对每天轿车停放辆次(每辆轿车每停放一次简称为“辆次”)与每辆轿车的收费情况进行调查,发现每辆次轿车的停车费定价不超过10元时,每天来此停放的轿车都为300辆次.若每辆次轿车的停车费定价超过10元,则每超过1元,每天来此停放的轿车就减少12辆次,设每辆次轿车的停车费为x元(为便于结算,停车费x只取整数),此停车场的日净收入为y元(日净收入=每天共收停车费-每天固定的支出),回答下列问题:
(1)①当x≤10时,y与x的关系式为: .
②当x>10时,y与x的关系式为: .
(2)停车场能否实现3000元的日净收入 如能实现,求出每辆次轿车的停车费定价,如不能实现,请说明理由.
(3)该商场要求此停车场既要吸引顾客,使每天轿车停放的辆次较多,又要有最大的日净收入,按此要求,每辆次轿车的停车费定价应定为多少元 此时最大日净收入是多少元
(1)①当x≤10时,y与x的关系式为: .
②当x>10时,y与x的关系式为:__________________________
.
y=300x-600
y=[300-12(x-10)]x-600,即
y=-12x2+420x-600.
(2)停车场能否实现3000元的日净收入 如能实现,求出每辆次轿车的停车费定价,如不能实现,请说明理由.
解:(2)依题意有:①当x≤10时,300x-600=3000,
解得x=12,不符合题意;
②x>10时,-12x2+420x-600=3000,
解得x1=15,x2=20.
故停车场能实现3000元的日净收入,每辆次轿车的停车费定价是15元或20元.
(3)该商场要求此停车场既要吸引顾客,使每天轿车停放的辆次较多,又要有最大的日净收入,按此要求,每辆次轿车的停车费定价应定为多少元 此时最大日净收入是多少元
解:(3)当x≤10时,停车300辆次,最大日净收入
y=300×10-600=2400(元).
当x>10时,y=-12x2+420x-600=-12(x-17.5)2+3075,
∴当x=17.5时,y有最大值,但x只能取整数,∴x取17或18.
显然,x取17或18时,此时最大日净收入为
y=-12×0.25+3075=3072(元).
∵需要轿车停放辆次较多,∴每辆次轿车的停车费定价应定为17元,此时最大日净收入是3072元.
例3 某学校小组利用暑假中前40天参加社会实践活动,参与了一家网上书店经营,了解到一种成本为每本20元的书在x天销售量P=50-x.在第x天的售价为每本y元,y与x的关系如图Z2-5所示.已知当社会实践活动
时间超过一半后,y=20+.
(1)请求出当1≤x≤20时,y与x的函数关系式,
并求出第12天此书的销售单价;
(2)这40天中该网点销售此书第几天获得的
利润最大 最大利润是多少
类型三
最大利润问题
图Z2-5
(1)请求出当1≤x≤20时,y与x的函数关系式,并求出第12天此书的销售单价;
图Z2-5
解:(1)当1≤x≤20时,设y=kx+b,将(1,30.5),
(20,40)代入,得解得
则y与x的函数关系式为:y=x+30(1≤x≤20),
当x=12时,y=6+30=36.
∴第12天此书的销售单价为36元.
(2)这40天中该网点销售此书第几天获得的利润最大 最大利润是多少
图Z2-5
解:(2)设该网店第x天获得的利润为w元.
当1≤x≤20时,w=(x+30-20)(50-x)=-x2+15x+500
=-(x-15)2+,∵-<0,∴当x=15时,w有最大值w1,且w1=612.5.
当21≤x≤40时,w=(20+-20)(50-x)=-315.
∵15750>0,∴随x的增大而减小,∴x=21时,最大.
于是,x=21时,w有最大值w2,且w2=-315=435.∵w1>w2,
∴这40天中该网点销售此书第15天获得的利润最大,最大利润是612.5元.
|题型精练|
1.[2022·连云港]某快餐店销售A,B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是
元.
1264
[解析]设每份A种快餐降价a元,则每天卖出(40+2a)份,每份B种快餐提高b元,则每天卖出(80-2b)份.
由题意,得40+2a+80-2b=40+80,解得a=b,
∴总利润W=(12-a)(40+2a)+(8+a)(80-2a)=-4a2+48a+1120
=-4(a-6)2+1264.
∵-4<0,∴当a=6时,W取得最大值1264,
即两种快餐一天的总利润最多为1264元.
2.[2022·聊城]为迎接建党一百周年,我市计划用两种花卉对某广场进行美化.已知用600元购买A种花卉与用900元购买B种花卉的数量相等,且B种花卉每盆比A种花卉多0.5元.
(1)A,B两种花卉每盆各多少元
(2)计划购买A,B两种花卉共6000盆,其中A种花卉的数量不超过B种花卉数量的,求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元.
(1)A,B两种花卉每盆各多少元
解:(1)设A种花卉每盆x元,则B种花卉每盆(x+0.5)元.
根据题意,得=.
解这个方程,得x=1.
经检验知,x=1是原分式方程的根,且符合题意.此时x+0.5=1.5(元).
所以,A种花卉每盆1元,B种花卉每盆1.5元.
(2)计划购买A,B两种花卉共6000盆,其中A种花卉的数量不超过B种花卉数量的,求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元.
解:(2)设购买A种花卉t盆,则购买B种花卉(6000-t)盆,设购买这批花卉的总费用为w元,则t≤(6000-t),解得t≤1500.
由题意,得w=t+1.5(6000-t)=-0.5t+9000.
因为w是t的一次函数,k=-0.5<0,所以w随t的增大而减小,
所以当t=1500时,w最小.w最小=-0.5×1500+9000=8250(元).
所以,购买A种花卉1500盆时购买这批花卉总费用最低,最低费用为8250元.
3.[2022·大连]某电商销售某种商品一段时间后,发现该商品每天的销售量y(单位:千克)和每千克的售价x(单位:元)满足一次函数关系(如图Z2-6所示),其中50≤x≤80.
(1)求y关于x的函数解析式;
(2)若该种商品的成本为每千克40元,该电
商如何定价才能使每天获得的利润最大
最大利润是多少
图Z2-6
(1)求y关于x的函数解析式;
图Z2-6
解:(1)设y=kx+b,将(50,100)、(80,40)代入,
得解得
∴y关于x的函数解析式为
y=-2x+200(50≤x≤80).
(2)若该种商品的成本为每千克40元,该电商如何定价才能使每天获得的利润最大 最大利润是多少
图Z2-6
解:(2)设电商每天获得的利润为w元,
则w=(x-40)(-2x+200)=-2x2+280x-8000=-2(x-70)2+1800.
∵-2<0,且对称轴是直线x=70,50≤x≤80,
∴当x=70时,w取得最大值,最大值为1800.
答:该电商定价该商品的售价为每千克70元时每天获得的利润最大,最大利润是1800元.
例4 [2022·河南]暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下:
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用
按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用
为y1(元),且y1=k1x+b;按照方案二所需费用为
y2(元),且y2=k2x.其函数图像如图Z2-7所示.
类型四
方案设计问题
图Z2-7
(1)求k1和b的值,并说明它们的实际意义.
(2)求打折前的每次健身费用和k2的值.
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少 说明理由.
(1)求k1和b的值,并说明它们的实际意义.
图Z2-7
解:(1)∵直线y1=k1x+b经过(0,30)和(10,180)
两点,
∴解得:
k1表示每次健身费用按六折优惠后的费用为
15元,b表示暑期专享卡每张30元.
(2)求打折前的每次健身费用和k2的值.
解(2)∵每次健身费用按六折优惠后的费用
为15元,
∴打折前的每次健身费用为15÷0.6=25(元).
∵不购买学生暑期专享卡,每次健身费用按
八折优惠,
∴k2=25×0.8=20.
图Z2-7
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少 说明理由.
解:(3)当x=8时,y1=15x+30=15×8+30=150,
y2=20x=20×8=160,
∵150<160,
∴选择方案一所需费用更少.
图Z2-7
|题型精练|
[2022·连云港]为了做好防疫工作,学校准备购进一批消毒液.已知2瓶A型消毒液和3瓶B型消毒液共需41元,5瓶A型消毒液和2瓶B型消毒液共需53元.
(1)这两种消毒液的单价各是多少元
(2)学校准备购进这两种消毒液共90瓶,且B型消毒液的数量不
少于A型消毒液数量的,请设计出最省钱的购买方案,并求出
最少费用.
(1)这两种消毒液的单价各是多少元
解:(1)设A型消毒液的单价是x元,B型消毒液的单价是y元,
由题意得 解得
答:A型消毒液的单价是7元,B型消毒液的单价是9元.
(2)学校准备购进这两种消毒液共90瓶,且B型消毒液的数量不
少于A型消毒液数量的,请设计出最省钱的购买方案,并求出
最少费用.
解:(2)设购进A型消毒液a瓶,费用为w元,则购进B型消毒液(90-a)瓶,依题意可得:w=7a+9(90-a)=-2a+810,
∴w随a的增大而减小.
∵B型消毒液的数量不少于A型消毒液数量的,
∴90-a≥a,解得a≤67.5,∴当x=67时,w取得最小值,此时,
w=-2×67+810=676,90-a=23,
答:最省钱的购买方案是购进A型消毒液67瓶,购进B型消毒液23瓶,最低费用为676元.
例5 [2022·无锡]有一块矩形地块ABCD,AB=20米,BC=30米.为美观,拟种植不同的花卉,如图Z2-8所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE和CDHG中种
植乙种花卉;在矩形EFGH中种植丙种花卉.甲、
乙、丙三种花卉的种植成本分别为20元/米2、60
元/米2、40元/米2,设三种花卉的种植总成本为y元.
类型五
几何面积问题
图Z2-8
(1)当x=5时,求种植总成本y;
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120米2,求三种花卉的最低种植总成本.
(1)当x=5时,求种植总成本y;
图Z2-8
解:(1)当x=5时,EF=20-2x=10,
EH=30-2x=20,
y=2×(EH+AD)×x×20+2×(GH+CD)×
x×60+EF·EH×40
=(20+30)×5×20+(10+20)×5×60+20×10×40=22000.
(2)求种植总成本y与x的函数表达式,并写出自变量x的取值范围;
图Z2-8
解:(2)EF=20-2x,EH=30-2x,
由题意得:y=2×(30+30-2x)·x·20+
2×(20+20-2x)·x·60+(30-2x)(20-2x)·40
=-400x+24000(0
图Z2-8
解:(3)甲种花卉的种植面积
S甲=2×(EH+AD)×x=(30-2x+30)x=-2x2+60x,
同理乙种花卉的种植面积S乙=-2x2+40x,
∵甲、乙两种花卉的种植面积之差不超过120米2,
∴-2x2+60x-(-2x2+40x)≤120,解得:x≤6,故0
故当x=6时,y的最小值为21600,
即三种花卉的最低种植总成本为21600元.
|题型精练|
[2022·沭阳模拟]如图Z2-9,在Rt△ABC中,∠A=90°,AB=8 cm,AC=6 cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B,A重合的情况),运动速度为2 cm/s,过点D作DE∥BC交AC于点E,连接BE,设动点D运动的时间为x(s),AE的长为y(cm).
(1)求y关于x的函数表达式,并写出自变量x
的取值范围.
(2)当x为何值时,△BDE的面积S有最大值
最大值为多少
图Z2-9
(1)求y关于x的函数表达式,并写出自变量x的取值范围.
图Z2-9
解:(1)动点D运动x s后,BD=2x.
∵AB=8,∴AD=8-2x.
∵DE∥BC,∴=,
∴AE==6-x,
∴y关于x的函数表达式为y=-x+6(0
图Z2-9
解:(2)S=·BD·AE
=×2x(-x+6)=-x2+6x
=-(x-2)2+6(0
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
