2021-2022学年鲁教版(五四制)九年级数学上册3.5 确定二次函数的表达式(1)课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学上册3.5 确定二次函数的表达式(1)课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 349.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 11:09:51 | ||
图片预览






文档简介
(共16张PPT)
3.5 确定二次函数的表达式(1)
学习目标
1.经历确定二次函数表达式的过程,体会求二次函数表达式的思想方法.
2.能根据已知条件,设出适当的二次函数表达式,从而更为便捷地解决问题.
重点:用待定系数法确定二次函数的表达式.
难点:根据条件特点,设出适当的二次函数表达式.
复习回顾
1.二次函数表达式的一般形式是什么
二次函数表达式的顶点式是什么
3.若抛物线与x轴两个交点的坐标为(x1,0),(x2,0),则其函数表达式可以表示成什么形式
y=ax +bx+c (a,b,c为常数,a≠0)
y=a(x-h)2+k (a≠0)
y=a(x-x1)(x-x2) (a≠0)
创设情境
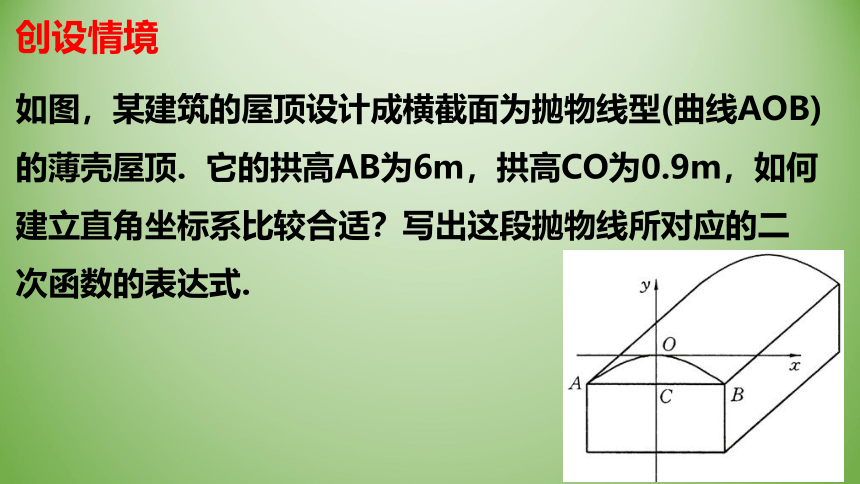
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶. 它的拱高AB为6m,拱高CO为0.9m,如何建立直角坐标系比较合适?写出这段抛物线所对应的二次函数的表达式.
讲解例题
例1 已知一个二次函数的图象的对称轴为x=-2,与y轴交点的纵坐标为2,且经过点(-3,-1),求这个二次函数的表达式.
解:设二次函数表达式为y=ax2+bx+c(a≠0)
∵ 与y轴交点的纵坐标为2
∴ c=2
∴ y=ax2+bx+2
∵ 图象的对称轴为x=-2
∴ -=-2,即b=4a ①
∵二次函数的图象经过点(-3,-1),
∴ 9a-3b+2=-1 ②
由①②,得a=1,b=4
∴ 二次函数表达式为y=x2+4x+2 .
跟踪练习1
已知抛物线与x轴相交于点A(-3,0),对称轴是直线x=-1,
且过点(2,5),求这个二次函数的表达式.
解:设二次函数表达式为y=ax2+bx+c(a≠0)
∵ 与x轴相交于点A(-3,0)
∴ 9a-3b+c=0 ①
∵ 图象的对称轴为x=-1
∴ -=-1 ,即b= 2a ②
∵二次函数的图象经过点(2,5)
∴ 4a+2b+c=5 ③
由①②③,得a=1,b=2,c=-3
∴ 二次函数表达式为y=x2+2x-3.
想一想
如果二次函数y=ax2+bx+c (a≠0)的图象的顶点坐标为(h,k),那么这个二次函数的表达式可表示成什么形式?
y=a(x-h)2+k (a≠0)
这个式子叫做二次函数的顶点式.
讲解例题
例2 已知一个二次函数的图象的顶点坐标是(-1,-6),并且该图象经过点(2,3),求这个二次函数的解析式.
解:∵ 图象的顶点坐标是(-1,-6)
∴ 可设二次函数得解析式为 y=a(x+1)2-6
∵ 函数图象过点(2,3)
∴ a(2+1)2 -6= 3
∴ a= 1
∴ 二次函数的解析式为y= (x+1)2 -6.
跟踪练习2
解:∵ 图象的顶点坐标是(-1,4)
∴可设二次函数得解析式为 y=a(x+1)2+4
∵ 函数图象过点(2,-5)
∴ a(2+1)2 +4= -5
∴ a= -1
∴ 二次函数的解析式为 y=- (x+1)2 +4
已知二次函数的图象以A (-1,4)为顶点,并且该图象经过点(2,-5),求该函数的表达式.
想一想
例1 已知一个二次函数的图象的对称轴为x=-2,与y轴交点的纵坐标为2,且经过点(-3,-1),求这个二次函数的表达式.
跟踪练习1 已知抛物线与x轴相交于点A(-3,0),对称轴是直线x=-1,且过点(2,5),求这个二次函数的表达式.
以上题目中给出了抛物线的对称轴,如果设y=a(x-h)2+k ,你能解决这两个问题吗?
解决问题
解:以线段AB的中垂线为y轴,以过点o且与y轴垂直的直线为x轴,建立直角坐标系.
设它的函数表达式为 y=ax (a≠0).
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶。它的拱高AB为6m,拱高CO为0.9m,如何建立直角坐标系比较合适?写出这段抛物线所对应的二次函数的表达式.
∵ AB=6 ∴ CB==3
又∵ OC=0.9
∴ B(3,-0.9)
∴ -0.9=a×3 ,a=-0.1
∴这段抛物线所对应的二次函数函数表达式为 y=-0.1x (-3≤x ≤ 3).
议一议
你能否总结出上述解题的一般步骤
1.若无坐标系,应先建立适当的直角坐标系;
2.设抛物线的表达式;
3.写出相关点的坐标;
4.列方程(或方程组);
5.解方程或方程组,求待定系数;
6.写出函数的表达式.
根据下列条件,分别求出对应的二次函数表达式:
(1)已知图象的顶点是坐标原点,且图象经过点(2,-5).
(2)已知图象的顶点坐标是(-1,-2),且图象经过点(1,10).
(3)抛物线的对称轴是直线x=-2,且经过(-1, -1), (-4,0)两点.
做一做
课堂小结
如何正确设定二次函数表达式 :
(1)已知二次函数的图象的顶点在坐标原点处,可以设二次函数的表达式为 .
(2)已知二次函数的图象的顶点在y轴上,可以设二次函数的表达式为 .
(3)已知二次函数的图象的顶点在x轴上,可以设二次函数的表达式为 .
(4)已知二次函数的图象的顶点不在坐标轴上,可以设二次函数的表达式为 .
2.确定二次函数表达式的一般方法是 .
当堂检测
1. 图象的顶点坐标为(-2,-2),且经过原点的二次函数表达式是( )
A.y= 0.5(x+2)2 –2 B.y= 0.5(x-2)2 –2
C.y= 2(x+2)2 –2 D.y= 2(x-2)2 –2
2. 已知一个二次函数的图象经过点(-1,6),并且当x=-3时,有最大值4,则该二次函数表达式为
.
3*. 已知抛物线与x轴只有1个交点(-2,0),且抛物线过点(0,4),求该抛物线表达式.
A
y=0.5(x+3)2+4
y= (x+2)2
布置作业
必做:课本P92 随堂练习
选做:课本P92 习题3.10
3.5 确定二次函数的表达式(1)
学习目标
1.经历确定二次函数表达式的过程,体会求二次函数表达式的思想方法.
2.能根据已知条件,设出适当的二次函数表达式,从而更为便捷地解决问题.
重点:用待定系数法确定二次函数的表达式.
难点:根据条件特点,设出适当的二次函数表达式.
复习回顾
1.二次函数表达式的一般形式是什么
二次函数表达式的顶点式是什么
3.若抛物线与x轴两个交点的坐标为(x1,0),(x2,0),则其函数表达式可以表示成什么形式
y=ax +bx+c (a,b,c为常数,a≠0)
y=a(x-h)2+k (a≠0)
y=a(x-x1)(x-x2) (a≠0)
创设情境
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶. 它的拱高AB为6m,拱高CO为0.9m,如何建立直角坐标系比较合适?写出这段抛物线所对应的二次函数的表达式.
讲解例题
例1 已知一个二次函数的图象的对称轴为x=-2,与y轴交点的纵坐标为2,且经过点(-3,-1),求这个二次函数的表达式.
解:设二次函数表达式为y=ax2+bx+c(a≠0)
∵ 与y轴交点的纵坐标为2
∴ c=2
∴ y=ax2+bx+2
∵ 图象的对称轴为x=-2
∴ -=-2,即b=4a ①
∵二次函数的图象经过点(-3,-1),
∴ 9a-3b+2=-1 ②
由①②,得a=1,b=4
∴ 二次函数表达式为y=x2+4x+2 .
跟踪练习1
已知抛物线与x轴相交于点A(-3,0),对称轴是直线x=-1,
且过点(2,5),求这个二次函数的表达式.
解:设二次函数表达式为y=ax2+bx+c(a≠0)
∵ 与x轴相交于点A(-3,0)
∴ 9a-3b+c=0 ①
∵ 图象的对称轴为x=-1
∴ -=-1 ,即b= 2a ②
∵二次函数的图象经过点(2,5)
∴ 4a+2b+c=5 ③
由①②③,得a=1,b=2,c=-3
∴ 二次函数表达式为y=x2+2x-3.
想一想
如果二次函数y=ax2+bx+c (a≠0)的图象的顶点坐标为(h,k),那么这个二次函数的表达式可表示成什么形式?
y=a(x-h)2+k (a≠0)
这个式子叫做二次函数的顶点式.
讲解例题
例2 已知一个二次函数的图象的顶点坐标是(-1,-6),并且该图象经过点(2,3),求这个二次函数的解析式.
解:∵ 图象的顶点坐标是(-1,-6)
∴ 可设二次函数得解析式为 y=a(x+1)2-6
∵ 函数图象过点(2,3)
∴ a(2+1)2 -6= 3
∴ a= 1
∴ 二次函数的解析式为y= (x+1)2 -6.
跟踪练习2
解:∵ 图象的顶点坐标是(-1,4)
∴可设二次函数得解析式为 y=a(x+1)2+4
∵ 函数图象过点(2,-5)
∴ a(2+1)2 +4= -5
∴ a= -1
∴ 二次函数的解析式为 y=- (x+1)2 +4
已知二次函数的图象以A (-1,4)为顶点,并且该图象经过点(2,-5),求该函数的表达式.
想一想
例1 已知一个二次函数的图象的对称轴为x=-2,与y轴交点的纵坐标为2,且经过点(-3,-1),求这个二次函数的表达式.
跟踪练习1 已知抛物线与x轴相交于点A(-3,0),对称轴是直线x=-1,且过点(2,5),求这个二次函数的表达式.
以上题目中给出了抛物线的对称轴,如果设y=a(x-h)2+k ,你能解决这两个问题吗?
解决问题
解:以线段AB的中垂线为y轴,以过点o且与y轴垂直的直线为x轴,建立直角坐标系.
设它的函数表达式为 y=ax (a≠0).
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶。它的拱高AB为6m,拱高CO为0.9m,如何建立直角坐标系比较合适?写出这段抛物线所对应的二次函数的表达式.
∵ AB=6 ∴ CB==3
又∵ OC=0.9
∴ B(3,-0.9)
∴ -0.9=a×3 ,a=-0.1
∴这段抛物线所对应的二次函数函数表达式为 y=-0.1x (-3≤x ≤ 3).
议一议
你能否总结出上述解题的一般步骤
1.若无坐标系,应先建立适当的直角坐标系;
2.设抛物线的表达式;
3.写出相关点的坐标;
4.列方程(或方程组);
5.解方程或方程组,求待定系数;
6.写出函数的表达式.
根据下列条件,分别求出对应的二次函数表达式:
(1)已知图象的顶点是坐标原点,且图象经过点(2,-5).
(2)已知图象的顶点坐标是(-1,-2),且图象经过点(1,10).
(3)抛物线的对称轴是直线x=-2,且经过(-1, -1), (-4,0)两点.
做一做
课堂小结
如何正确设定二次函数表达式 :
(1)已知二次函数的图象的顶点在坐标原点处,可以设二次函数的表达式为 .
(2)已知二次函数的图象的顶点在y轴上,可以设二次函数的表达式为 .
(3)已知二次函数的图象的顶点在x轴上,可以设二次函数的表达式为 .
(4)已知二次函数的图象的顶点不在坐标轴上,可以设二次函数的表达式为 .
2.确定二次函数表达式的一般方法是 .
当堂检测
1. 图象的顶点坐标为(-2,-2),且经过原点的二次函数表达式是( )
A.y= 0.5(x+2)2 –2 B.y= 0.5(x-2)2 –2
C.y= 2(x+2)2 –2 D.y= 2(x-2)2 –2
2. 已知一个二次函数的图象经过点(-1,6),并且当x=-3时,有最大值4,则该二次函数表达式为
.
3*. 已知抛物线与x轴只有1个交点(-2,0),且抛物线过点(0,4),求该抛物线表达式.
A
y=0.5(x+3)2+4
y= (x+2)2
布置作业
必做:课本P92 随堂练习
选做:课本P92 习题3.10
