2.2基本不等式 强化训练-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案)
文档属性
| 名称 | 2.2基本不等式 强化训练-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 324.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 11:42:32 | ||
图片预览


文档简介
2022-2023学年高一第一学期(新人教A版)
2.2基本不等式 强化训练
一、单项选择题(每小题5分,共40分)
1、已知,则y的最小值为( )
A.2 B.3 C.4 D.5
2、下列不等式恒成立的是
A. B.
C. D.
3、已知,那么的最小值是( )
A、 B、 C、 D、
4、已知正实数a、b满足,则的最小值是( )
A. B. C. 3 D. 5
5、若,则下列说法一定正确的是( )
A、 B、
C、的最小值为2 D、
6、已知方程(为实数)有两个正实数根,
则的最小值是( )
A、 B、 C、 D、
7、已知某产品的总成本(单位:元)与年产量(单位:件)之间的关系为. 设该产品年产量为时的平均成本为(单位:元/件),则的最小值是( )
A、 B、 C、 D、
8、已知,,,且,则的最小值为( )
A.16 B.12 C.10 D.8
二、多项选择题(每小题5分,共20分,有多项符合要求,全部选对得5分,部分选对得2分,有选错得0分)
9、若,下列不等式恒成立的是( )
A. B.
C. D.
10、已知,,且.则下列选项正确的是( )
A.的最小值为
B.的最小值为
C.
D.的最大值为
11、已知正实数a,b满足,则以下不等式正确的是( )
A. B.
C. D.
12、已知,,且,则下列结论正确的是( )
A、 B、的最小值为8
C、ab的最小值为16 D、的最小值为2
二、填空题(每小题5分,共20分)
13、已知,则函数的最小值为________.
14、若两个正数x,y满足=1,并且x+2y>2m--1恒成立,则实数m的取值范围是___
15、设,则的最小值为______________.
16、已知正实数a,b满足a+b=1,则的最小值为 .
三 解答题(共6小题,共计70分)
17、(10分)已知正数a, b满足a+b=1。
(1)求ab的取值范围;
(2)求的最小值.
18.(12分)设a, b, c且a+b+c=1,求证:
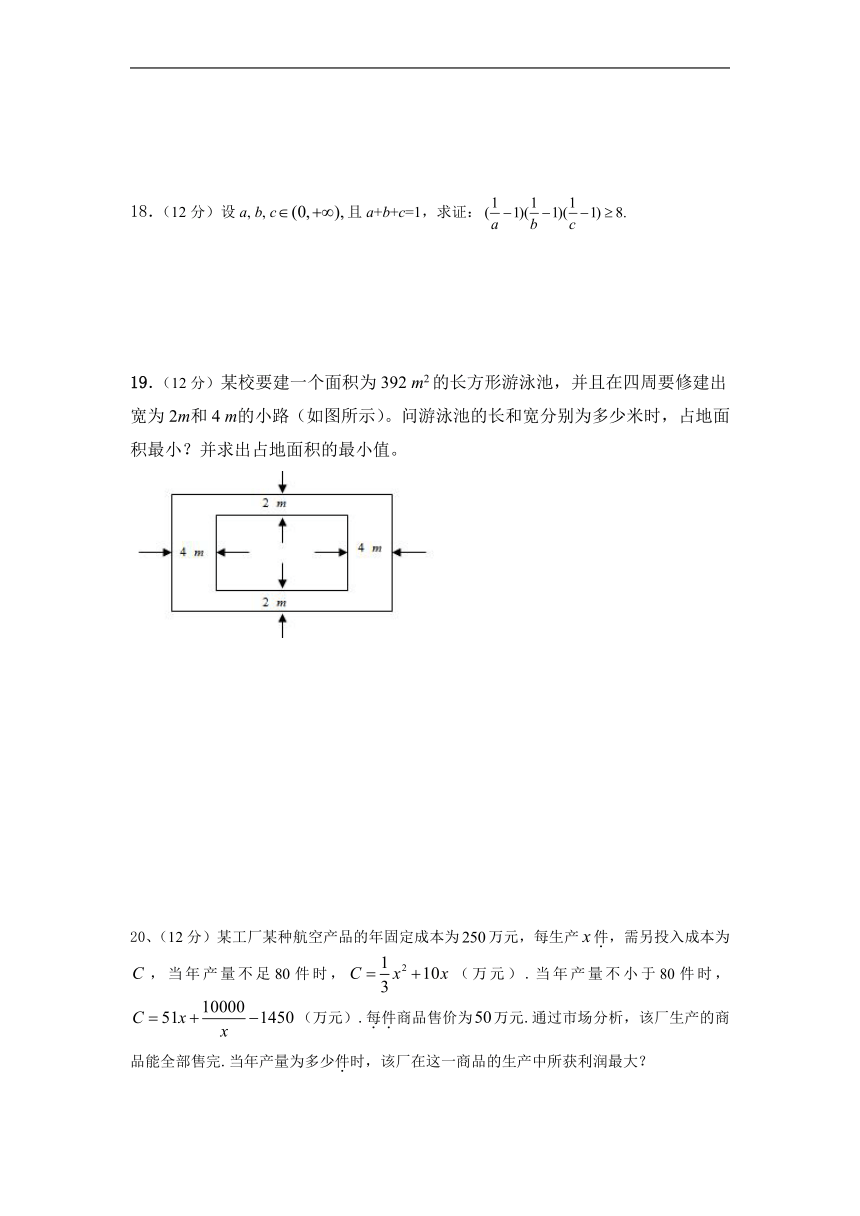
19.(12分)某校要建一个面积为392 m2的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,占地面积最小?并求出占地面积的最小值。
20、(12分)某工厂某种航空产品的年固定成本为万元,每生产件,需另投入成本为,当年产量不足件时,(万元).当年产量不小于件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.当年产量为多少件时,该厂在这一商品的生产中所获利润最大?
21、(12分)计划建造一个室内面积为1500平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为x米,两个养殖池的总面积为y平方米,如图所示,当x取何值时,y取最大值?最大值是多少
22、(12分)某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的)和两个半圆构成,设,且.
若内圈周长为,则取何值时,矩形的面积最大?
参考答案
1、D 2、D 3、A 4、C 5、D 6、B 7、B 8、A
9、AC 10、BD 11、BD 12、AC
13、5 14、m< 15、9 16、11
17、(1)1=,得,当时取等号,
又因为a, b为正数,
所以,ab的取值范围为
(2) =,
当,即时,的最小值为18.
18、证明:
当且仅当时取等号。
19、解:设游泳池的长为x m,则游泳池的宽为m,
又设占地面积为y m2,依题意,得=424+4(x+)≥424+224=648 当且仅当x=即x=28时取“=”.
答:游泳池的长为28 m宽为m时,占地面积最小为648 m2。
20、解:设该厂在这一商品的生产中所获利润为L,
当时,
利润为:
此时,当时,取得最大值万元.
当时,
利润为:
此时,当且仅当时,即时,取得最大值万元,
因为,所以年产量为件时,利润最大为万元.
21、解:依题意得温室的另一边长为米.
因此养殖池的总面积,
因为解得
因为,
所以,
当且仅当,即时上式等号成立,
所以.
当时,.
当x为30时,y取最大值为1215.
22、设半圆形半径为,矩形的面积为,内圈周长为.
由题意知:,且,即,
于是
当且仅当时,等号成立.
答:当时,矩形的面积最大.
2.2基本不等式 强化训练
一、单项选择题(每小题5分,共40分)
1、已知,则y的最小值为( )
A.2 B.3 C.4 D.5
2、下列不等式恒成立的是
A. B.
C. D.
3、已知,那么的最小值是( )
A、 B、 C、 D、
4、已知正实数a、b满足,则的最小值是( )
A. B. C. 3 D. 5
5、若,则下列说法一定正确的是( )
A、 B、
C、的最小值为2 D、
6、已知方程(为实数)有两个正实数根,
则的最小值是( )
A、 B、 C、 D、
7、已知某产品的总成本(单位:元)与年产量(单位:件)之间的关系为. 设该产品年产量为时的平均成本为(单位:元/件),则的最小值是( )
A、 B、 C、 D、
8、已知,,,且,则的最小值为( )
A.16 B.12 C.10 D.8
二、多项选择题(每小题5分,共20分,有多项符合要求,全部选对得5分,部分选对得2分,有选错得0分)
9、若,下列不等式恒成立的是( )
A. B.
C. D.
10、已知,,且.则下列选项正确的是( )
A.的最小值为
B.的最小值为
C.
D.的最大值为
11、已知正实数a,b满足,则以下不等式正确的是( )
A. B.
C. D.
12、已知,,且,则下列结论正确的是( )
A、 B、的最小值为8
C、ab的最小值为16 D、的最小值为2
二、填空题(每小题5分,共20分)
13、已知,则函数的最小值为________.
14、若两个正数x,y满足=1,并且x+2y>2m--1恒成立,则实数m的取值范围是___
15、设,则的最小值为______________.
16、已知正实数a,b满足a+b=1,则的最小值为 .
三 解答题(共6小题,共计70分)
17、(10分)已知正数a, b满足a+b=1。
(1)求ab的取值范围;
(2)求的最小值.
18.(12分)设a, b, c且a+b+c=1,求证:
19.(12分)某校要建一个面积为392 m2的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,占地面积最小?并求出占地面积的最小值。
20、(12分)某工厂某种航空产品的年固定成本为万元,每生产件,需另投入成本为,当年产量不足件时,(万元).当年产量不小于件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.当年产量为多少件时,该厂在这一商品的生产中所获利润最大?
21、(12分)计划建造一个室内面积为1500平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为x米,两个养殖池的总面积为y平方米,如图所示,当x取何值时,y取最大值?最大值是多少
22、(12分)某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的)和两个半圆构成,设,且.
若内圈周长为,则取何值时,矩形的面积最大?
参考答案
1、D 2、D 3、A 4、C 5、D 6、B 7、B 8、A
9、AC 10、BD 11、BD 12、AC
13、5 14、m< 15、9 16、11
17、(1)1=,得,当时取等号,
又因为a, b为正数,
所以,ab的取值范围为
(2) =,
当,即时,的最小值为18.
18、证明:
当且仅当时取等号。
19、解:设游泳池的长为x m,则游泳池的宽为m,
又设占地面积为y m2,依题意,得=424+4(x+)≥424+224=648 当且仅当x=即x=28时取“=”.
答:游泳池的长为28 m宽为m时,占地面积最小为648 m2。
20、解:设该厂在这一商品的生产中所获利润为L,
当时,
利润为:
此时,当时,取得最大值万元.
当时,
利润为:
此时,当且仅当时,即时,取得最大值万元,
因为,所以年产量为件时,利润最大为万元.
21、解:依题意得温室的另一边长为米.
因此养殖池的总面积,
因为解得
因为,
所以,
当且仅当,即时上式等号成立,
所以.
当时,.
当x为30时,y取最大值为1215.
22、设半圆形半径为,矩形的面积为,内圈周长为.
由题意知:,且,即,
于是
当且仅当时,等号成立.
答:当时,矩形的面积最大.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
