4.4.1对数函数的概念 课件(共25张PPT)
文档属性
| 名称 | 4.4.1对数函数的概念 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 683.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 14:01:24 | ||
图片预览








文档简介
(共25张PPT)
4.4 对数函数
4.4.1 对数函数的概念
明确目标 发展素养
1.通过具体实例,了解对数函数的概念. 2.会求对数函数的定义域、值域. 1.通过学习对数函数的概念,培养数学抽象素养.
2.借助对数函数的定义域的求解,培养数学运算素养.
(一)教材梳理填空
1.对数函数的概念:
一般地,函数y= (a>0,且a≠1)叫做对数函数,其中x是自变量,定义域为(0,+∞).
[微思考] 含有对数符号“log”的函数就是对数函数,对吗?
提示:不对,判断一个函数是否是对数函数不仅要含有对数符号“log”,还要符合对数函数的形式.
logax
2.特殊的对数函数:
常用对数函数 以 为底的对数函数 _______
自然对数函数 以 为底的对数函数________
10
y=lg x
无理数e
y=ln x
2.下列函数是对数函数的是 ( )
A.y=log2x B.y=ln(x+1)
C.y=logxe D.y=logxx
答案:A
3.函数f(x)=ln(x2-x)的定义域为 ( )
A.(0,1) B.(0,1]
C.(-∞,0)∪(1,+∞) D.(-∞,0)∪[1,+∞)
解析:由x2-x>0,可得x>1或x<0,故函数f(x)的定义域为{x|x<0或x>1},故选C.
答案:C
4.若对数函数的图象过点P(9,2),则此对数函数的解析式为________.
解析:设对数函数为y=logax(a>0,且a≠1),∴2=loga9,∴a=3,∴解析式为y=log3x.
答案:y=log3x
题型一 对数函数的概念
【学透用活】
对数函数概念的注意点
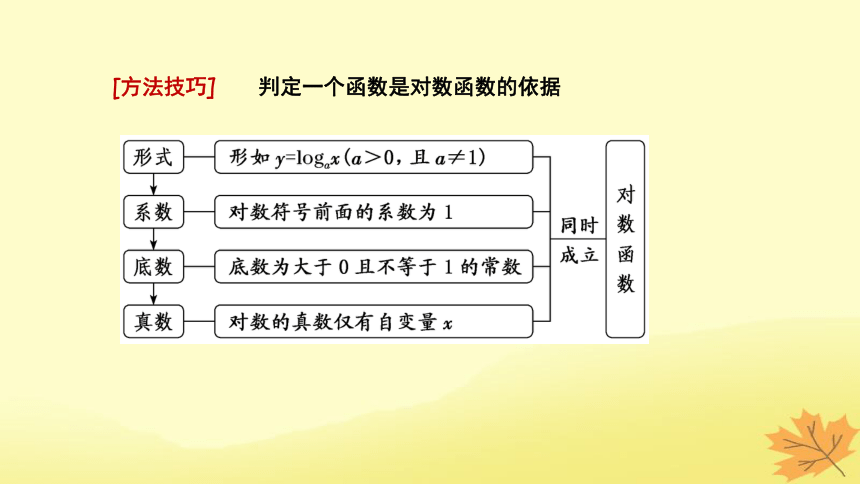
[方法技巧] 判定一个函数是对数函数的依据
【对点练清】
1.下列函数是对数函数的是 ( )
A.y=loga(2x) B.y=log22x
C.y=logx4 D.y=lg x
解析:选项A、B、C中的函数都不具有“y=logax(a>0,且a≠1)”的形式,只有D选项符合.
答案:D
2.函数f(x)=(a2-a+1)log(a+1)x是对数函数,则实数a=________.
解析:a2-a+1=1,解得a=0或1.
又a+1>0,且a+1≠1,∴a=1.
答案:1
题型二 对数型函数的定义域
[探究发现]
(1)对数函数y=logax的定义域是什么?
提示:y=logax的定义域是{x|x>0}.
(2)对数函数y=logax的底数a有什么要求?
提示:y=logax的底数a>0,且a≠1.
【学透用活】
[典例2] 求下列函数的定义域:
(1)y=loga(3-x)+loga(3+x);
(2)y=log2(16-4x);(3)y=log(1-x)5.
[方法技巧]
求对数型函数定义域的原则
(1)分母不能为0.
(2)根指数为偶数时,被开方数非负.
(3)对数的真数大于0,底数大于0且不为1.
(4)若需对函数进行变形,则需先求出定义域,再对函数进行恒等变形.
[方法技巧]
实际问题中对数模型要建模准确,计算时应充分利用对数的运算性质,注意变量的实际意义.
【对点练清】
某公司制订了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式;
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元?
【课堂思维激活】
一、综合性——强调融会贯通
1.若函数y=loga(x+a)(a>0且a≠1)的图象过点(-1,0).
(1)求a的值;
(2)求函数的定义域.
4.4 对数函数
4.4.1 对数函数的概念
明确目标 发展素养
1.通过具体实例,了解对数函数的概念. 2.会求对数函数的定义域、值域. 1.通过学习对数函数的概念,培养数学抽象素养.
2.借助对数函数的定义域的求解,培养数学运算素养.
(一)教材梳理填空
1.对数函数的概念:
一般地,函数y= (a>0,且a≠1)叫做对数函数,其中x是自变量,定义域为(0,+∞).
[微思考] 含有对数符号“log”的函数就是对数函数,对吗?
提示:不对,判断一个函数是否是对数函数不仅要含有对数符号“log”,还要符合对数函数的形式.
logax
2.特殊的对数函数:
常用对数函数 以 为底的对数函数 _______
自然对数函数 以 为底的对数函数________
10
y=lg x
无理数e
y=ln x
2.下列函数是对数函数的是 ( )
A.y=log2x B.y=ln(x+1)
C.y=logxe D.y=logxx
答案:A
3.函数f(x)=ln(x2-x)的定义域为 ( )
A.(0,1) B.(0,1]
C.(-∞,0)∪(1,+∞) D.(-∞,0)∪[1,+∞)
解析:由x2-x>0,可得x>1或x<0,故函数f(x)的定义域为{x|x<0或x>1},故选C.
答案:C
4.若对数函数的图象过点P(9,2),则此对数函数的解析式为________.
解析:设对数函数为y=logax(a>0,且a≠1),∴2=loga9,∴a=3,∴解析式为y=log3x.
答案:y=log3x
题型一 对数函数的概念
【学透用活】
对数函数概念的注意点
[方法技巧] 判定一个函数是对数函数的依据
【对点练清】
1.下列函数是对数函数的是 ( )
A.y=loga(2x) B.y=log22x
C.y=logx4 D.y=lg x
解析:选项A、B、C中的函数都不具有“y=logax(a>0,且a≠1)”的形式,只有D选项符合.
答案:D
2.函数f(x)=(a2-a+1)log(a+1)x是对数函数,则实数a=________.
解析:a2-a+1=1,解得a=0或1.
又a+1>0,且a+1≠1,∴a=1.
答案:1
题型二 对数型函数的定义域
[探究发现]
(1)对数函数y=logax的定义域是什么?
提示:y=logax的定义域是{x|x>0}.
(2)对数函数y=logax的底数a有什么要求?
提示:y=logax的底数a>0,且a≠1.
【学透用活】
[典例2] 求下列函数的定义域:
(1)y=loga(3-x)+loga(3+x);
(2)y=log2(16-4x);(3)y=log(1-x)5.
[方法技巧]
求对数型函数定义域的原则
(1)分母不能为0.
(2)根指数为偶数时,被开方数非负.
(3)对数的真数大于0,底数大于0且不为1.
(4)若需对函数进行变形,则需先求出定义域,再对函数进行恒等变形.
[方法技巧]
实际问题中对数模型要建模准确,计算时应充分利用对数的运算性质,注意变量的实际意义.
【对点练清】
某公司制订了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式;
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元?
【课堂思维激活】
一、综合性——强调融会贯通
1.若函数y=loga(x+a)(a>0且a≠1)的图象过点(-1,0).
(1)求a的值;
(2)求函数的定义域.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
