4.4.3不同函数增长的差异 课件(共27张PPT)
文档属性
| 名称 | 4.4.3不同函数增长的差异 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 583.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 14:02:56 | ||
图片预览








文档简介
(共27张PPT)
4.4.3 不同函数增长的差异
明确目标 发展素养
1.理解直线上升、指数爆炸、对数增长的含义. 2.区分指数函数、对数函数以及一次函数增长速度的差异. 3.会选择适当的函数模型分析和解决一些实际问题. 借助三个函数模型的增长特征,培养数学运算和数学建模素养.
(一)教材梳理填空
函数 y=kx(k>0) y=ax(a>1) y=logax(a>1)
在(0,+∞) 上的增减性 __________ __________ _________
随x的增大 函数图象 保持固定的增长速度 逐渐与 _____平行 逐渐与 _____平行
单调递增
单调递增
单调递增
y轴
x轴
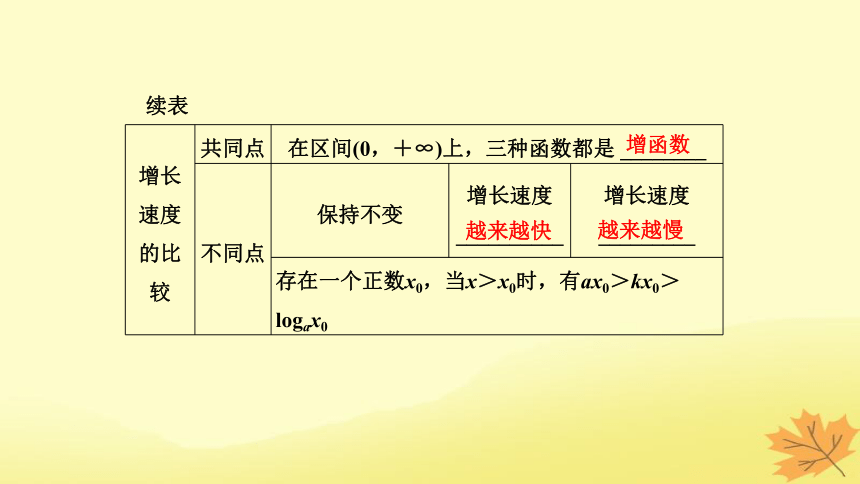
增长速度的比较 共同点 在区间(0,+∞)上,三种函数都是 ________ 不同点 保持不变 增长速度__________ 增长速度_________
存在一个正数x0,当x>x0时,有ax0>kx0>logax0 增函数
越来越快
越来越慢
续表
(二)基本知能小试
1.判断正误:
(1)对任意的x>0,kx>logax. ( )
(2)对任意的x>0,ax>logax. ( )
(3)函数y=log2x增长的速度越来越慢. ( )
答案:(1)× (2)× (3)√
2.下列函数中随x的增大而增大且速度最快的是 ( )
A.y=ex B.y=ln x
C.y=3x D.y=e-x
答案:A
3.某公司为了适应市场需求,对产品结构进行了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与产量x的关系,则可选用 ( )
A.一次函数模型 B.二次函数模型
C.指数函数模型 D.对数函数模型
答案:D
4.某种产品每件80元,每天可售出30件,如果每件定价120元,则每天可售出20件,如果售出件数是定价的一次函数,则这个函数解析式为________________.
题型一 三类函数模型增长差异的比较
【学透用活】
[典例1] (1)下列函数中,增长速度最快的是 ( )
A.y=2 021x B.y=x2 021
C.y=log2 021x D.y=2 021x
(2)四个自变量y1,y2,y3,y4随变量x变化的数据如表所示:
则关于x呈指数型函数变化的变量是________.
x 1 5 10 15 20 25 30
y1 2 26 101 226 401 626 901
y2 2 32 1 024 32 768 1.05×106 3.36×107 1.07×109
y3 2 10 20 30 40 50 60
y4 2 4.322 5.322 5.907 6.322 6.644 6.907
[解析] (1)比较一次函数、幂函数、指数函数与对数函数可知,指数函数增长速度最快,故选A.
(2)以爆炸式增长的变量呈指数函数变化.从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,且都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,画出它们的图象(图略),可知变量y2关于x呈指数型函数变化.
[答案] (1)A (2)y2
[方法技巧]
比较函数增长情况的方法
(1)解析法:直接看函数解析式是一次函数、指数型函数还是对数型函数,其中当x较大时,指数型函数增长速度最快,一次函数增长速度其次,对数型函数增长速度最慢.
(2)表格法:通过分析表格中的数据得出函数增长速度的差异.
(3)图象法:在同一直角坐标系中画出各函数的图象,观察图象并借助计算器,便能直观地得出这几个函数增长速度的差异.
【对点练清】
1.下列函数中,增长速度越来越慢的是 ( )
A.y=6x B.y=log6x
C.y=x2 D.y=6x
解析:D中一次函数的增长速度不变,A、C中函数的增长速度越来越快,只有B中对数函数的增长速度越来越慢,符合题意.
答案:B
2.“红豆生南国,春来发几枝”.如图给出了红豆生长时间t(月)与枝数y的关系图,那么最适合拟合红豆的枝数与生长时间的关系的函数是 ( )
A.指数函数y=2t
B.对数函数y=log2t
C.幂函数y=t3
D.二次函数y=2t2
解析:根据已知所给的关系图,观察得到图象在第一象限,且从左到右图象是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可得,用指数函数拟合最好,故选A.
答案:A
题型二 函数模型的选择
【学透用活】
[典例2] 某学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但奖金总数不超过3万元,同时奖金不超过利润的20%.现有三个奖励模型:y=0.2x,y=log5x,y=1.02x,其中哪个模型符合该校的要求?
[解] 作出函数y=3,y=0.2x,y=log5x,y=1.02x的图象(如图所示).观察图象可知,在区间[5,60]上,y=0.2x,y=1.02x的图象都有一部分在直线y=3的上方,只有y=log5x的图象始终在y=3和y=0.2x的下方,这说明只有按模型y=log5x进行奖励才符合学校的要求.
[方法技巧]
几类不同增长函数模型选择的方法
(1)增长速度不变,即自变量增加相同量时,函数值的增量相等,此时的函数模型是一次函数模型.
(2)增长速度越来越快,即自变量增加相同量时,函数值的增量成倍增加,此时的函数模型是指数函数模型.
(3)增长速度越来越慢,即自变量增加相同量时,函数值的增量越来越小,此时的函数模型是对数函数模型.
【对点练清】
某人对东北一种松树的生长进行了研究,收集了其高度h(米)与生长时间t(年)的相关数据,选择h=mt+b与h=loga(t+1)来拟合h与t的关系,你认为哪个符合?并预测第8年的松树高度.
t/年 1 2 3 4 5 6
h/米 0.6 1 1.3 1.5 1.6 1.7
解:在坐标轴上标出t(年)与h(米)之间的关系如图所示.
由图象可以看出增长的速度越来越慢,用一次函数模型
拟合不合适,则选用对数函数模型比较合理.
不妨将(2,1)代入h=loga(t+1)中,得1=loga3,解得a=3.
故可用函数h=log3(t+1)来拟合这个实际问题.
当t=8时,求得h=log3(8+1)=2,
故可预测第8年松树的高度为2米.
题型三 不同增长的函数模型的图象特征
【学透用活】
[典例3] 函数f(x)=lg x,g(x)=0.3x-1的图象如图所示.
(1)指出图中C1,C2分别对应哪一个函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
[解] (1)由函数图象特征及变化趋势,知曲线C1对应的函数为g(x)=0.3x-1,
曲线C2对应的函数为f(x)=lg x.
(2)当x∈(0,x1)时,g(x)>f(x);当x∈(x1,x2)时,g(x)<f(x);当x∈(x2,+∞)时,g(x)>f(x).
g(x)呈直线增长,函数值变化是均匀的;f(x)随着x的增大而逐渐增大,其函数值变化得越来越慢.
[方法技巧]
由图象判断一次函数、指数函数和对数函数的方法
根据图象判断增长型的一次函数、指数函数和对数函数时,通常是观察函数图象上升得快慢,即随着自变量的增大,图象最“陡”的函数是指数函数,图象趋于平缓的函数是对数函数.
【课堂思维激活】
一、应用性——强调学以致用
1.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
解:设第x天所得回报是y元.
由题意,方案一:y=40(x∈N+);
方案二:y=10x(x∈N+);
方案三:y=0.4×2x-1(x∈N+).
作出三个函数的图象如图:
由图可以看出,从每天回报看,在第一天到第三天,方案一最多,在第四天,方案一、二一样多,方案三最少,在第五天到第八天,方案二最多,第九天开始,方案三比其他两个方案所得回报多得多,经验证到第三十天,所得回报已超过2亿元,
∴若是短期投资可选择方案一或方案二,长期的投资则选择方案三.
通过计算器计算列出三种方案的累积收入表.
∴投资一天到六天,应选方案一,投资七天方案一、二均可,投资八天到十天应选方案二,投资十一天及其以上,应选方案三.
二、创新性——强调创新意识和创新思维
2.已知甲、乙两物体在同一直线上向同一方向做匀速
直线运动,其位移y(单位:km)和运动时间x(单
位:h)(0≤x≤5)的关系如图所示,给出以下说法:
①甲、乙运动的速度相同,都是5 km/h;
②甲、乙运动的时间相同,开始运动后相等时间内甲的位移比乙大;
③甲、乙运动的时间相同,乙的速度是4 km/h;
④当甲、乙运动了3 h后,甲的位移比乙大3 km,但乙在甲前方2 km处.
其中正确的说法是 ( )
A.③ B.①②③
C.①③④ D.②③④
解析:经图象分析③是对的,故①错;对于②,甲、乙运动的时间显然都是5 h,因为甲的速度为5 km/h,乙的速度为4 km/h,所以开始运动相等时间内甲的位移比乙大,故②正确;对于④,当甲、乙运动了3 h后,甲的位移为3×5=15(km),乙的位移为3×4=12(km).又因为乙是从甲前方5 km处开始运动的,所以甲的位移比乙大3 km,但乙在甲前方2 km处,所以④正确.
答案:D
4.4.3 不同函数增长的差异
明确目标 发展素养
1.理解直线上升、指数爆炸、对数增长的含义. 2.区分指数函数、对数函数以及一次函数增长速度的差异. 3.会选择适当的函数模型分析和解决一些实际问题. 借助三个函数模型的增长特征,培养数学运算和数学建模素养.
(一)教材梳理填空
函数 y=kx(k>0) y=ax(a>1) y=logax(a>1)
在(0,+∞) 上的增减性 __________ __________ _________
随x的增大 函数图象 保持固定的增长速度 逐渐与 _____平行 逐渐与 _____平行
单调递增
单调递增
单调递增
y轴
x轴
增长速度的比较 共同点 在区间(0,+∞)上,三种函数都是 ________ 不同点 保持不变 增长速度__________ 增长速度_________
存在一个正数x0,当x>x0时,有ax0>kx0>logax0 增函数
越来越快
越来越慢
续表
(二)基本知能小试
1.判断正误:
(1)对任意的x>0,kx>logax. ( )
(2)对任意的x>0,ax>logax. ( )
(3)函数y=log2x增长的速度越来越慢. ( )
答案:(1)× (2)× (3)√
2.下列函数中随x的增大而增大且速度最快的是 ( )
A.y=ex B.y=ln x
C.y=3x D.y=e-x
答案:A
3.某公司为了适应市场需求,对产品结构进行了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与产量x的关系,则可选用 ( )
A.一次函数模型 B.二次函数模型
C.指数函数模型 D.对数函数模型
答案:D
4.某种产品每件80元,每天可售出30件,如果每件定价120元,则每天可售出20件,如果售出件数是定价的一次函数,则这个函数解析式为________________.
题型一 三类函数模型增长差异的比较
【学透用活】
[典例1] (1)下列函数中,增长速度最快的是 ( )
A.y=2 021x B.y=x2 021
C.y=log2 021x D.y=2 021x
(2)四个自变量y1,y2,y3,y4随变量x变化的数据如表所示:
则关于x呈指数型函数变化的变量是________.
x 1 5 10 15 20 25 30
y1 2 26 101 226 401 626 901
y2 2 32 1 024 32 768 1.05×106 3.36×107 1.07×109
y3 2 10 20 30 40 50 60
y4 2 4.322 5.322 5.907 6.322 6.644 6.907
[解析] (1)比较一次函数、幂函数、指数函数与对数函数可知,指数函数增长速度最快,故选A.
(2)以爆炸式增长的变量呈指数函数变化.从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,且都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,画出它们的图象(图略),可知变量y2关于x呈指数型函数变化.
[答案] (1)A (2)y2
[方法技巧]
比较函数增长情况的方法
(1)解析法:直接看函数解析式是一次函数、指数型函数还是对数型函数,其中当x较大时,指数型函数增长速度最快,一次函数增长速度其次,对数型函数增长速度最慢.
(2)表格法:通过分析表格中的数据得出函数增长速度的差异.
(3)图象法:在同一直角坐标系中画出各函数的图象,观察图象并借助计算器,便能直观地得出这几个函数增长速度的差异.
【对点练清】
1.下列函数中,增长速度越来越慢的是 ( )
A.y=6x B.y=log6x
C.y=x2 D.y=6x
解析:D中一次函数的增长速度不变,A、C中函数的增长速度越来越快,只有B中对数函数的增长速度越来越慢,符合题意.
答案:B
2.“红豆生南国,春来发几枝”.如图给出了红豆生长时间t(月)与枝数y的关系图,那么最适合拟合红豆的枝数与生长时间的关系的函数是 ( )
A.指数函数y=2t
B.对数函数y=log2t
C.幂函数y=t3
D.二次函数y=2t2
解析:根据已知所给的关系图,观察得到图象在第一象限,且从左到右图象是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可得,用指数函数拟合最好,故选A.
答案:A
题型二 函数模型的选择
【学透用活】
[典例2] 某学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且奖金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但奖金总数不超过3万元,同时奖金不超过利润的20%.现有三个奖励模型:y=0.2x,y=log5x,y=1.02x,其中哪个模型符合该校的要求?
[解] 作出函数y=3,y=0.2x,y=log5x,y=1.02x的图象(如图所示).观察图象可知,在区间[5,60]上,y=0.2x,y=1.02x的图象都有一部分在直线y=3的上方,只有y=log5x的图象始终在y=3和y=0.2x的下方,这说明只有按模型y=log5x进行奖励才符合学校的要求.
[方法技巧]
几类不同增长函数模型选择的方法
(1)增长速度不变,即自变量增加相同量时,函数值的增量相等,此时的函数模型是一次函数模型.
(2)增长速度越来越快,即自变量增加相同量时,函数值的增量成倍增加,此时的函数模型是指数函数模型.
(3)增长速度越来越慢,即自变量增加相同量时,函数值的增量越来越小,此时的函数模型是对数函数模型.
【对点练清】
某人对东北一种松树的生长进行了研究,收集了其高度h(米)与生长时间t(年)的相关数据,选择h=mt+b与h=loga(t+1)来拟合h与t的关系,你认为哪个符合?并预测第8年的松树高度.
t/年 1 2 3 4 5 6
h/米 0.6 1 1.3 1.5 1.6 1.7
解:在坐标轴上标出t(年)与h(米)之间的关系如图所示.
由图象可以看出增长的速度越来越慢,用一次函数模型
拟合不合适,则选用对数函数模型比较合理.
不妨将(2,1)代入h=loga(t+1)中,得1=loga3,解得a=3.
故可用函数h=log3(t+1)来拟合这个实际问题.
当t=8时,求得h=log3(8+1)=2,
故可预测第8年松树的高度为2米.
题型三 不同增长的函数模型的图象特征
【学透用活】
[典例3] 函数f(x)=lg x,g(x)=0.3x-1的图象如图所示.
(1)指出图中C1,C2分别对应哪一个函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
[解] (1)由函数图象特征及变化趋势,知曲线C1对应的函数为g(x)=0.3x-1,
曲线C2对应的函数为f(x)=lg x.
(2)当x∈(0,x1)时,g(x)>f(x);当x∈(x1,x2)时,g(x)<f(x);当x∈(x2,+∞)时,g(x)>f(x).
g(x)呈直线增长,函数值变化是均匀的;f(x)随着x的增大而逐渐增大,其函数值变化得越来越慢.
[方法技巧]
由图象判断一次函数、指数函数和对数函数的方法
根据图象判断增长型的一次函数、指数函数和对数函数时,通常是观察函数图象上升得快慢,即随着自变量的增大,图象最“陡”的函数是指数函数,图象趋于平缓的函数是对数函数.
【课堂思维激活】
一、应用性——强调学以致用
1.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
解:设第x天所得回报是y元.
由题意,方案一:y=40(x∈N+);
方案二:y=10x(x∈N+);
方案三:y=0.4×2x-1(x∈N+).
作出三个函数的图象如图:
由图可以看出,从每天回报看,在第一天到第三天,方案一最多,在第四天,方案一、二一样多,方案三最少,在第五天到第八天,方案二最多,第九天开始,方案三比其他两个方案所得回报多得多,经验证到第三十天,所得回报已超过2亿元,
∴若是短期投资可选择方案一或方案二,长期的投资则选择方案三.
通过计算器计算列出三种方案的累积收入表.
∴投资一天到六天,应选方案一,投资七天方案一、二均可,投资八天到十天应选方案二,投资十一天及其以上,应选方案三.
二、创新性——强调创新意识和创新思维
2.已知甲、乙两物体在同一直线上向同一方向做匀速
直线运动,其位移y(单位:km)和运动时间x(单
位:h)(0≤x≤5)的关系如图所示,给出以下说法:
①甲、乙运动的速度相同,都是5 km/h;
②甲、乙运动的时间相同,开始运动后相等时间内甲的位移比乙大;
③甲、乙运动的时间相同,乙的速度是4 km/h;
④当甲、乙运动了3 h后,甲的位移比乙大3 km,但乙在甲前方2 km处.
其中正确的说法是 ( )
A.③ B.①②③
C.①③④ D.②③④
解析:经图象分析③是对的,故①错;对于②,甲、乙运动的时间显然都是5 h,因为甲的速度为5 km/h,乙的速度为4 km/h,所以开始运动相等时间内甲的位移比乙大,故②正确;对于④,当甲、乙运动了3 h后,甲的位移为3×5=15(km),乙的位移为3×4=12(km).又因为乙是从甲前方5 km处开始运动的,所以甲的位移比乙大3 km,但乙在甲前方2 km处,所以④正确.
答案:D
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
