4.3.2对数的运算 课件(共34张PPT)
文档属性
| 名称 | 4.3.2对数的运算 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 14:04:06 | ||
图片预览







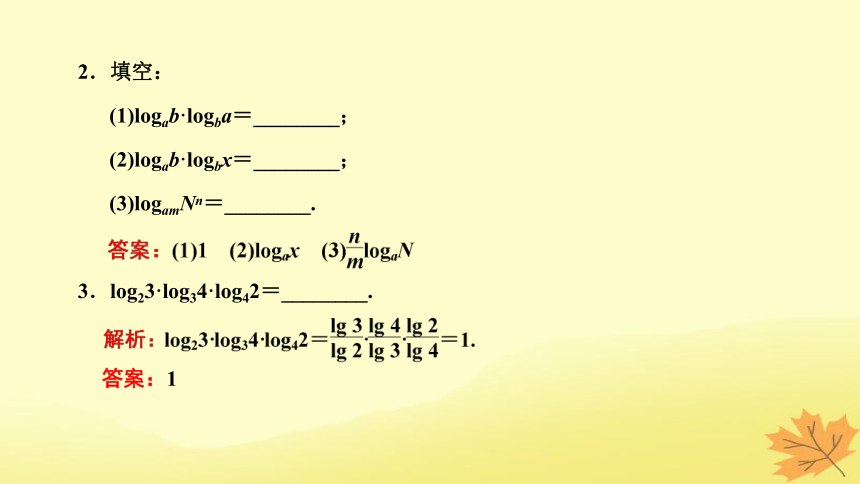

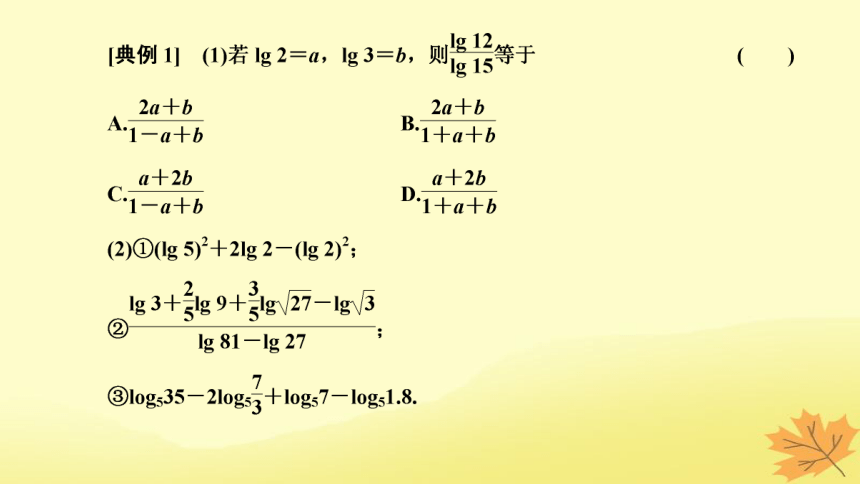
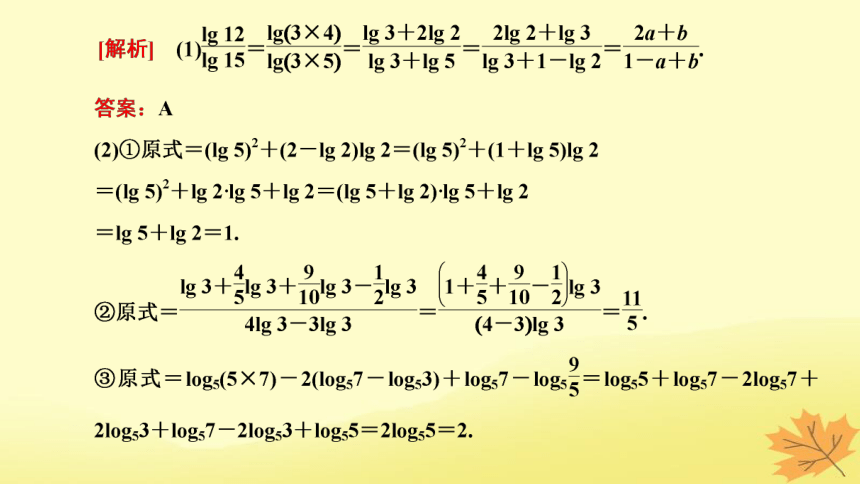

文档简介
(共34张PPT)
4.3.2 对数的运算
明确目标 发展素养
1.理解对数的运算性质. 2.能用换底公式将一般对数转化成自然对数或常用对数. 3.会运用运算性质进行一些简单的化简与证明. 1.借助对数的运算性质化简、求值,培养数学运算素养.
2.通过学习换底公式,培养逻辑推理素养.
logaM+logaN
logaM-logaN
nlogaM
[微提醒]
对数与指数运算对照表(a>0,且a≠1,m>0,N>0)
(二)基本知能小试
1.判断正误:
(1)log2x2=2log2x. ( )
(2)loga[(-2)×(-3)]=loga(-2)+loga(-3). ( )
(3)loga(xy)=logax·logay. ( )
(4)log2(-5)2=2log2(-5). ( )
答案:(1)× (2)× (3)× (3)×
2.计算log84+log82等于 ( )
A.log86 B.8 C.6 D.1
答案:D
知识点二 换底公式
(一)教材梳理填空
logab= (a>0,且a≠1;b>0;c>0,且c≠1).我们把上式叫做对数换底公式.
[微思考] 换底公式中底数c是特定数还是任意数?
提示:是大于0且不等于1的任意数.
2.填空:
(1)logab·logba=________;
(2)logab·logbx=________;
(3)logamNn=________.
3.log23·log34·log42=________.
答案:1
题型一 对数运算性质的应用
【学透用活】
1.对数运算性质的适用前提
对数的运算性质的适用条件是“同底,且真数为正”,即a>0,a≠1,M>0,N>0.若去掉此条件,性质不一定成立.
2.对数运算性质(1)的推广
性质(1)可以推广到若干个正因数的积:
loga(M1·M2·M3·…·Mn)=logaM1+logaM2+…+logaMn(a>0,且a≠1,Mi>0,i=1,2,…,n).
[方法技巧]
对数式化简与求值的基本原则和方法
基本原则 对数的化简求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行
常用方法 “收”,将同底的两对数的和(差)收成积(商)的对数
“拆”,将积(商)的对数拆成同底的两对数的和(差)
[方法技巧] 利用换底公式进行化简求值的原则和技巧
【对点练清】
1.若logab·logbc·logc3=2,则a的值为________.
[方法技巧]
1.解对数综合应用问题的3种方法
(1)统一化:所求为对数式,条件转为对数式.
(2)选底数:针对具体问题,选择恰当的底数.
(3)会结合:学会换底公式与对数运算法则结合使用.
2.解对数应用题的4个步骤
【课堂思维激活】
一、综合性——强调融会贯通
1.设a,b,c是直角三角形的三边,其中c为斜边,且c+b≠1,c-b≠1,求证:log(c+b)a+log(c-b)a=2log(c+b)a·log(c-b)a.
二、应用性——强调学以致用
2.[好题共享——选自苏教版新教材]如图,2000年我国国内生产总值(GDP)为89 442亿元.如果我国GDP年均增长7.8%,那么按照这个增长速度,在2000年的基础上,经过多少年以后,我国GDP就能实现比2000年翻两番的目标?
三、创新性——强调创新意识和创新思维
3.[好题共享——选自苏教版新教材]我们知道,任何一个正实数N可以表示成N=a×10n(1≤a<10,n∈Z),此时lg N=n+lg a(0≤lg a<1).当n>0时,N是n+1位数.
(1)试用上述方法,判断2100是多少位数(lg 2≈0.301 0);
(2)当n<0时,你有怎样的结论?
解:(1)N=2100>0,lg N=lg 2100=30.1.
∴n=30,lg a=0.1.∴n+1=31.
∴N是31位数.
(2)n<0时,N是-n位小数.
例如:N=0.002>0,N=2×10-3,lg N=-3+lg 2,
∴n=-3,显然N=0.002是三位小数.
4.3.2 对数的运算
明确目标 发展素养
1.理解对数的运算性质. 2.能用换底公式将一般对数转化成自然对数或常用对数. 3.会运用运算性质进行一些简单的化简与证明. 1.借助对数的运算性质化简、求值,培养数学运算素养.
2.通过学习换底公式,培养逻辑推理素养.
logaM+logaN
logaM-logaN
nlogaM
[微提醒]
对数与指数运算对照表(a>0,且a≠1,m>0,N>0)
(二)基本知能小试
1.判断正误:
(1)log2x2=2log2x. ( )
(2)loga[(-2)×(-3)]=loga(-2)+loga(-3). ( )
(3)loga(xy)=logax·logay. ( )
(4)log2(-5)2=2log2(-5). ( )
答案:(1)× (2)× (3)× (3)×
2.计算log84+log82等于 ( )
A.log86 B.8 C.6 D.1
答案:D
知识点二 换底公式
(一)教材梳理填空
logab= (a>0,且a≠1;b>0;c>0,且c≠1).我们把上式叫做对数换底公式.
[微思考] 换底公式中底数c是特定数还是任意数?
提示:是大于0且不等于1的任意数.
2.填空:
(1)logab·logba=________;
(2)logab·logbx=________;
(3)logamNn=________.
3.log23·log34·log42=________.
答案:1
题型一 对数运算性质的应用
【学透用活】
1.对数运算性质的适用前提
对数的运算性质的适用条件是“同底,且真数为正”,即a>0,a≠1,M>0,N>0.若去掉此条件,性质不一定成立.
2.对数运算性质(1)的推广
性质(1)可以推广到若干个正因数的积:
loga(M1·M2·M3·…·Mn)=logaM1+logaM2+…+logaMn(a>0,且a≠1,Mi>0,i=1,2,…,n).
[方法技巧]
对数式化简与求值的基本原则和方法
基本原则 对数的化简求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行
常用方法 “收”,将同底的两对数的和(差)收成积(商)的对数
“拆”,将积(商)的对数拆成同底的两对数的和(差)
[方法技巧] 利用换底公式进行化简求值的原则和技巧
【对点练清】
1.若logab·logbc·logc3=2,则a的值为________.
[方法技巧]
1.解对数综合应用问题的3种方法
(1)统一化:所求为对数式,条件转为对数式.
(2)选底数:针对具体问题,选择恰当的底数.
(3)会结合:学会换底公式与对数运算法则结合使用.
2.解对数应用题的4个步骤
【课堂思维激活】
一、综合性——强调融会贯通
1.设a,b,c是直角三角形的三边,其中c为斜边,且c+b≠1,c-b≠1,求证:log(c+b)a+log(c-b)a=2log(c+b)a·log(c-b)a.
二、应用性——强调学以致用
2.[好题共享——选自苏教版新教材]如图,2000年我国国内生产总值(GDP)为89 442亿元.如果我国GDP年均增长7.8%,那么按照这个增长速度,在2000年的基础上,经过多少年以后,我国GDP就能实现比2000年翻两番的目标?
三、创新性——强调创新意识和创新思维
3.[好题共享——选自苏教版新教材]我们知道,任何一个正实数N可以表示成N=a×10n(1≤a<10,n∈Z),此时lg N=n+lg a(0≤lg a<1).当n>0时,N是n+1位数.
(1)试用上述方法,判断2100是多少位数(lg 2≈0.301 0);
(2)当n<0时,你有怎样的结论?
解:(1)N=2100>0,lg N=lg 2100=30.1.
∴n=30,lg a=0.1.∴n+1=31.
∴N是31位数.
(2)n<0时,N是-n位小数.
例如:N=0.002>0,N=2×10-3,lg N=-3+lg 2,
∴n=-3,显然N=0.002是三位小数.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
