4.2.2指数函数的图象和性质 课件(共38张PPT)
文档属性
| 名称 | 4.2.2指数函数的图象和性质 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 14:07:21 | ||
图片预览










文档简介
(共38张PPT)
4.2.2 指数函数的图象和性质
明确目标 发展素养
1.掌握指数函数的定义域、值域的求法. 2.能画出具体的指数函数的图象,并根据指数函数的图象说出指数函数的性质. 3.掌握指数函数的性质并会应用,能利用函数的单调性比较大小. 1.通过学习指数函数的图象,培养直观想象素养.
2.借助指数函数的定义域、值域的求法,培养数学运算和逻辑推理素养.
3.借助指数函数的性质及应用,培养逻辑推理和数学运算素养.
(一)教材梳理填空
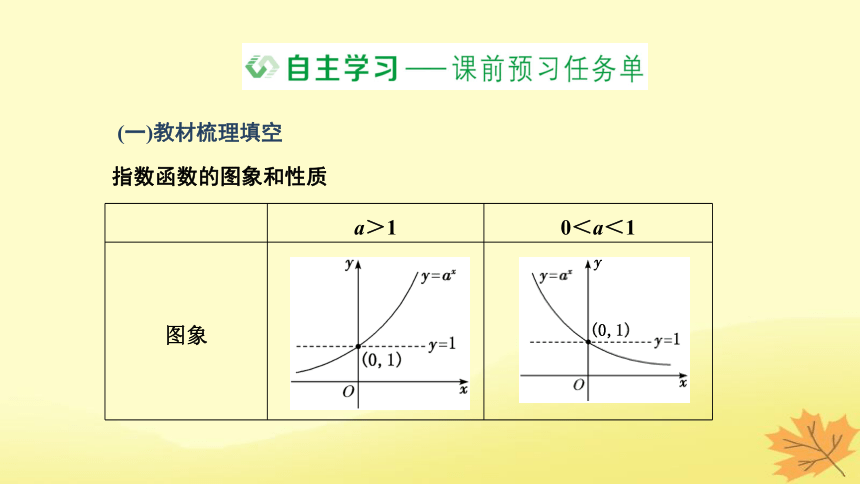
指数函数的图象和性质
a>1 0<a<1
图象
性 质 定义域 R 值域 _________ 过定点 ,即当x=0时,y=__ 单调性 在R上是 _______ 在R上是 _______
奇偶性 非奇非偶函数 对称性 函数y=ax与y=a-x的图象关于 对称 续表
(0,+∞)
(0,1)
1
增函数
减函数
y轴
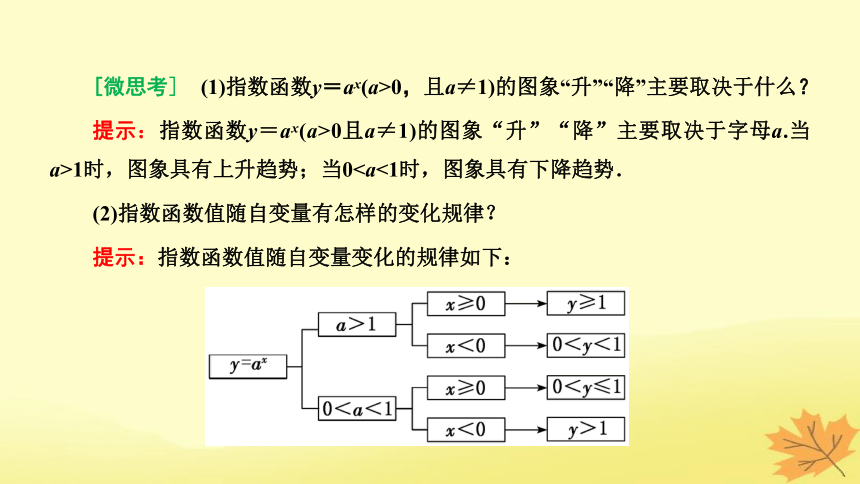
[微思考] (1)指数函数y=ax(a>0,且a≠1)的图象“升”“降”主要取决于什么?
提示:指数函数y=ax(a>0且a≠1)的图象“升”“降”主要取决于字母a.当a>1时,图象具有上升趋势;当0(2)指数函数值随自变量有怎样的变化规律?
提示:指数函数值随自变量变化的规律如下:
提醒:(1)通过建立不等关系求定义域时,要注意解集为各不等关系解集的交集.
(2)当指数型函数的底数含字母时,在求定义域、值域时要注意分类讨论.
题型二 指数函数的图象及应用
【学透用活】
1.指数函数图象的特征
同一坐标系中,画出不同底数的指数函数的图象如图所示.直线x=1与四个指数函数y=ax,y=bx,y=cx,y=dx的交点依次为(1,a),(1,b),(1,c),(1,d),所以有0<b<a<1<d<c,因此可得出以下结论:在y轴的右侧,底数越大,图象越高,简称“底大图高”.
2.指数函数图象的变换
(1)平移规律:设b>0,
(2)对称规律:
y=ax(a>0,且a≠1) 的图象 与y=a-x的图象关于y轴对称
与y=-ax的图象关于x轴对称
与y=-a-x的图象关于坐标原点对称
[方法技巧]
指数函数图象问题的处理技巧
(1)抓住图象上的特殊点,如指数函数的图象过定点.
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移).
(3)利用函数的奇偶性与单调性.奇偶性确定函数的对称情况,单调性决定函数图象的走势.
【对点练清】
1.已知0A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:函数恒过点(0,1+b),因为b<-1,所以点(0,1+b)在y轴负半轴上.故图象不经过第一象限.
答案:A
2.已知直线y=2a与函数y=|2x-2|的图象有两个公共点,则实数a的取值范围为________.
解析:函数y=|2x-2|的图象如图所示.要使直线y=2a与该图象有两个公共点,则有0<2a<2,即0<a<1,故实数a的取值范围为(0,1).
答案:(0,1)
3.画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.
(1)y=2x+1;(2)y=-2x.
解:画出函数的图象如图所示.
(1)y=2x+1的图象是由y=2x的图象向上平移1
个单位长度得到的.
(2)y=-2x的图象与y=2x的图象关于x轴对称.
题型三 指数函数的简单应用
【分类例析】
角度(一) 比较大小
[典例3] 比较下列各题中两个值的大小:
(1)1.70.3,0.93.1;(2)-1.8,-2.5;
(3)0.20.3,0.30.2.
[方法技巧]
角度(二) 解指数不等式
[典例4] 求满足下列条件的x的取值范围:
(1)3x-1>9x;(2)0.2x<25;
(3)a-5x>ax+7(a>0,且a≠1).
[解] (1)∵3x-1>9x,∴3x-1>32x,
又y=3x在定义域R上是增函数,
∴x-1>2x,∴x<-1.即x的取值范围是(-∞,-1).
[方法技巧] 指数不等式的三种求解方法
性质法 解形如ax>ab的不等式,可借助函数y=ax的单调性求解,如果a的取值不确定,需分a>1与0隐含 性质法 解形如ax>b的不等式,可先将b转化为以a为底数的指数幂的形式,再借助函数y=ax的单调性求解
图象法 解形如ax>bx的不等式,可利用对应的函数图象求解
(2)分情况讨论:
①当0∴x2-3x+1>x+6,
∴x2-4x-5>0,解得x<-1或x>5.
②当a>1时,函数f(x)=ax在R上是增函数,
∴x2-3x+1∴x2-4x-5<0,解得-1综上所述,当0{x|x<-1或x>5};
当a>1时,x的取值范围是{x|-1【课堂思维激活】
一、综合性——强调融会贯通
1.已知a,b,c,m都是正数,am=bm+cm,当m取何值时,长分别为a,b,c的三条线段能构成三角形?
二、应用性——强调学以致用
2.[好题共享——选自苏教版新教材]有些家用电器(如冰箱等)使用了氟化物,氟化物的释放破坏了大气上层的臭氧层,使臭氧含量Q呈指数函数型变化,在氟化物排放量维持某种水平时,具有关系式Q=Q0e-0.002 5t,其中Q0是臭氧的初始量.
(1)随时间t的增加,臭氧的含量是增加还是减少?
(2)试估计多少年以后将会有一半的臭氧消失.(用计算器计算)
[析题建模]
解:(1)画出y=h(x),y=p(x)的图象如图所示.
4个函数都是y=ax(a>0,a≠1)的形式,它们的性质有:
①定义域为R;
②值域为(0,+∞);
③都过定点(0,1);
④当a>1时,函数在定义域内单调递增,0<a<1时,
函数在定义域内单调递减;
⑤a>1时,若x<0,则0<y<1,若x>0,则y>1.
0<a<1时,若x>0,则0<y<1,若x<0,则y>1;
⑥对于函数y=ax(a>0,且a≠1),y=bx(b>0,且b≠1),
当a>b>1时,
若x<0,则0<ax<bx<1;若x=0,则ax=bx=1;
若x>0,则ax>bx>1.
当0<a<b<1时,
若x<0,则ax>bx>1;若x=0,则ax=bx=1;
若x>0,则0<ax<bx<1.
(2)举例:原来有一个细胞,细胞分裂的规则是细胞由一个分裂成2个,则经过x次分裂,细胞个数y,
则y=2x,是一个指数函数.
4.2.2 指数函数的图象和性质
明确目标 发展素养
1.掌握指数函数的定义域、值域的求法. 2.能画出具体的指数函数的图象,并根据指数函数的图象说出指数函数的性质. 3.掌握指数函数的性质并会应用,能利用函数的单调性比较大小. 1.通过学习指数函数的图象,培养直观想象素养.
2.借助指数函数的定义域、值域的求法,培养数学运算和逻辑推理素养.
3.借助指数函数的性质及应用,培养逻辑推理和数学运算素养.
(一)教材梳理填空
指数函数的图象和性质
a>1 0<a<1
图象
性 质 定义域 R 值域 _________ 过定点 ,即当x=0时,y=__ 单调性 在R上是 _______ 在R上是 _______
奇偶性 非奇非偶函数 对称性 函数y=ax与y=a-x的图象关于 对称 续表
(0,+∞)
(0,1)
1
增函数
减函数
y轴
[微思考] (1)指数函数y=ax(a>0,且a≠1)的图象“升”“降”主要取决于什么?
提示:指数函数y=ax(a>0且a≠1)的图象“升”“降”主要取决于字母a.当a>1时,图象具有上升趋势;当0
提示:指数函数值随自变量变化的规律如下:
提醒:(1)通过建立不等关系求定义域时,要注意解集为各不等关系解集的交集.
(2)当指数型函数的底数含字母时,在求定义域、值域时要注意分类讨论.
题型二 指数函数的图象及应用
【学透用活】
1.指数函数图象的特征
同一坐标系中,画出不同底数的指数函数的图象如图所示.直线x=1与四个指数函数y=ax,y=bx,y=cx,y=dx的交点依次为(1,a),(1,b),(1,c),(1,d),所以有0<b<a<1<d<c,因此可得出以下结论:在y轴的右侧,底数越大,图象越高,简称“底大图高”.
2.指数函数图象的变换
(1)平移规律:设b>0,
(2)对称规律:
y=ax(a>0,且a≠1) 的图象 与y=a-x的图象关于y轴对称
与y=-ax的图象关于x轴对称
与y=-a-x的图象关于坐标原点对称
[方法技巧]
指数函数图象问题的处理技巧
(1)抓住图象上的特殊点,如指数函数的图象过定点.
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移).
(3)利用函数的奇偶性与单调性.奇偶性确定函数的对称情况,单调性决定函数图象的走势.
【对点练清】
1.已知0
C.第三象限 D.第四象限
解析:函数恒过点(0,1+b),因为b<-1,所以点(0,1+b)在y轴负半轴上.故图象不经过第一象限.
答案:A
2.已知直线y=2a与函数y=|2x-2|的图象有两个公共点,则实数a的取值范围为________.
解析:函数y=|2x-2|的图象如图所示.要使直线y=2a与该图象有两个公共点,则有0<2a<2,即0<a<1,故实数a的取值范围为(0,1).
答案:(0,1)
3.画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.
(1)y=2x+1;(2)y=-2x.
解:画出函数的图象如图所示.
(1)y=2x+1的图象是由y=2x的图象向上平移1
个单位长度得到的.
(2)y=-2x的图象与y=2x的图象关于x轴对称.
题型三 指数函数的简单应用
【分类例析】
角度(一) 比较大小
[典例3] 比较下列各题中两个值的大小:
(1)1.70.3,0.93.1;(2)-1.8,-2.5;
(3)0.20.3,0.30.2.
[方法技巧]
角度(二) 解指数不等式
[典例4] 求满足下列条件的x的取值范围:
(1)3x-1>9x;(2)0.2x<25;
(3)a-5x>ax+7(a>0,且a≠1).
[解] (1)∵3x-1>9x,∴3x-1>32x,
又y=3x在定义域R上是增函数,
∴x-1>2x,∴x<-1.即x的取值范围是(-∞,-1).
[方法技巧] 指数不等式的三种求解方法
性质法 解形如ax>ab的不等式,可借助函数y=ax的单调性求解,如果a的取值不确定,需分a>1与0
图象法 解形如ax>bx的不等式,可利用对应的函数图象求解
(2)分情况讨论:
①当0
∴x2-4x-5>0,解得x<-1或x>5.
②当a>1时,函数f(x)=ax在R上是增函数,
∴x2-3x+1
当a>1时,x的取值范围是{x|-1
一、综合性——强调融会贯通
1.已知a,b,c,m都是正数,am=bm+cm,当m取何值时,长分别为a,b,c的三条线段能构成三角形?
二、应用性——强调学以致用
2.[好题共享——选自苏教版新教材]有些家用电器(如冰箱等)使用了氟化物,氟化物的释放破坏了大气上层的臭氧层,使臭氧含量Q呈指数函数型变化,在氟化物排放量维持某种水平时,具有关系式Q=Q0e-0.002 5t,其中Q0是臭氧的初始量.
(1)随时间t的增加,臭氧的含量是增加还是减少?
(2)试估计多少年以后将会有一半的臭氧消失.(用计算器计算)
[析题建模]
解:(1)画出y=h(x),y=p(x)的图象如图所示.
4个函数都是y=ax(a>0,a≠1)的形式,它们的性质有:
①定义域为R;
②值域为(0,+∞);
③都过定点(0,1);
④当a>1时,函数在定义域内单调递增,0<a<1时,
函数在定义域内单调递减;
⑤a>1时,若x<0,则0<y<1,若x>0,则y>1.
0<a<1时,若x>0,则0<y<1,若x<0,则y>1;
⑥对于函数y=ax(a>0,且a≠1),y=bx(b>0,且b≠1),
当a>b>1时,
若x<0,则0<ax<bx<1;若x=0,则ax=bx=1;
若x>0,则ax>bx>1.
当0<a<b<1时,
若x<0,则ax>bx>1;若x=0,则ax=bx=1;
若x>0,则0<ax<bx<1.
(2)举例:原来有一个细胞,细胞分裂的规则是细胞由一个分裂成2个,则经过x次分裂,细胞个数y,
则y=2x,是一个指数函数.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
