4.3.1对数的概念 课件(共26张PPT)
文档属性
| 名称 | 4.3.1对数的概念 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 755.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 14:07:52 | ||
图片预览








文档简介
(共26张PPT)
4.3 对数
4.3.1 对数的概念
明确目标 发展素养
1.理解对数的概念,掌握对数的性质,能进行简单的对数计算. 2.理解指数式与对数式的等价关系,会进行对数式与指数式的互化. 3.理解常用对数、自然对数的概念及记法. 1.借助指数式与对数式的互化,培养逻辑推理素养.
2.应用对数的性质解题,培养数学运算素养.
(一)教材梳理填空
1.对数的概念:
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x= ,其中a叫做对数的 ,N叫做 .
logaN
底数
真数
2.常用对数与自然对数:
名称 定义 记法
常用对数 以____为底的对数叫做常用对数 _
自然对数 以无理数e=2.718 28…为底的对数称为自然对数 _
10
lg N
ln N
3.对数的基本性质:
(1)当a>0,且a≠1时,ax=N .
(2)负数和0没有对数.
(3)特殊值:1的对数是 ,即loga1= ;底数的对数是1,即logaa=1.
(4)如果把ax=N中的x写成logaN,则有alogaN=N.(对数恒等式)
[微思考] 在对数的定义中,为什么不能取a≤0及a=1呢?
x=logaN
0
0
2.若a2=M(a>0,且a≠1),则有 ( )
A.log2M=a B.logaM=2 C.loga2=M D.log2a=M
答案:B
3.若log2x=2,则x=__________.
答案:4
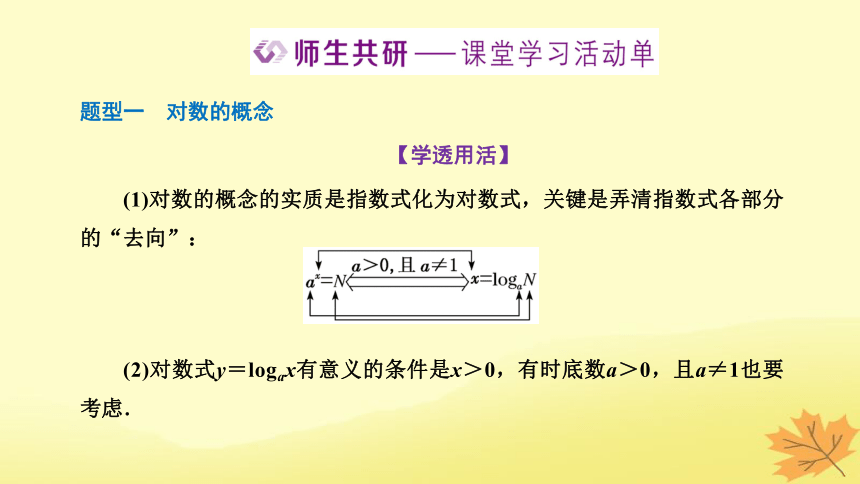
题型一 对数的概念
【学透用活】
(1)对数的概念的实质是指数式化为对数式,关键是弄清指数式各部分的“去向”:
(2)对数式y=logax有意义的条件是x>0,有时底数a>0,且a≠1也要考虑.
[方法技巧]
指数式与对数式互化的思路
(1)指数式化为对数式:将指数式的幂作为真数,指数作为对数,底数不变,写出对数式.
(2)对数式化为指数式:将对数式的真数作为幂,对数作为指数,底数不变,写出指数式.
[方法技巧]
利用指数与对数的互化求变量值的策略
(1)已知底数与指数,用指数式求幂.
(2)已知指数与幂,用指数式求底数.
(3)已知底数与幂,利用对数式表示指数.
题型三 对数的性质及对数恒等式
【学透用活】
[典例3] (1)求下列各式的值:
①2-log23;②e3ln 7;③lg 0.0012.
(2)求下列各式中x的值:
①log3(lg x)=1;②log3(log4(log5x))=0.
[方法技巧]
利用对数性质求解的两类问题的解法
(1)求多重对数式的值解题方法是由内到外,如求loga(logbc)的值,先求logbc的值,再求loga(logbc)的值.
(2)已知多重对数式的值,求变量值,应从外到内求,逐步脱去“log”后再求解.
2.[变设问]在本例(2)②条件下,计算625 log x3的值为________.
解析:因为x=625,则625 log 6253=3.
答案:3
3.[变条件]本例(2)②中若将“log3(log4(log5x))=0”改为“3log3(log4(log5x))=1”,则x=________.
解析:由3log3(log4(log5x))=1可得log4(log5x)=1,故log5x=4,所以x=54=625.
答案:625
【课堂思维激活】
一、综合性——强调融会贯通
1.某同学解等式“log(x-2)(x2-7x+13)=0中的x”,过程如下:
提示:不正确.忽略对数的底数a>0,且a≠1.
二、应用性——强调学以致用
2.分贝是计量声音强度相对大小的单位,物理学家引入了声压级来描述声音的大小;把声压p0=2×10-5帕作为参考声压.把所要测量的声压p与参考声压p0的比值取常用对数后乘20得到的数值成为声压级,声压级是听力学中最重要的参数之一,单位是分贝(dB),分贝值在60以下为无害区,60~110为过渡区,110以上为有害区.
(1)根据上述材料,列出分贝值y与声压p的函数关系式.
(2)某地声压p=0.002帕,试问:该地为以上所说的什么区?
(3)某电视台,现场录制节目时,现场多次响起响亮的掌声,某观众用仪器测量到最响亮的一次音量达到了90分贝,试求此时中央电视台演播大厅的声压是多少?
[析题建模]
三、创新性——强调创新意识和创新思维
3.对于任意实数x,符号[x]表示x的整数部分,即[x]是不超过x的最大整数.在实数轴R(箭头向右)上[x]是在点x左侧的第一个整数点,当x是整数时[x]就是x.这个函数[x]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用.求[lg 1]+[lg 2]+[lg 3]+…+[lg 10]+[lg 11]+[lg 12]+…+[lg 2 019]的值.
解:根据定义,[lg 1]=[lg 2]=[lg 3]=…[lg 9]=0;
[lg 10]=[lg 11]=[lg 12]=…[lg 99]=1;
[lg 100]=[lg 101]=[lg 102]=…=[lg 999]=2,
[lg 1 000]=[lg 1 001]=[lg 1 002]=…[lg 2 019]=3.
所以[lg 1]+[lg 2]+[lg 3]+…+[lg 10]+[lg 11]+[lg 12]+…+[lg 2 019]=1×(99-9)+2×(999-99)+3×(2 019-999)=90+2×900+3×1 020=4 950.
4.3 对数
4.3.1 对数的概念
明确目标 发展素养
1.理解对数的概念,掌握对数的性质,能进行简单的对数计算. 2.理解指数式与对数式的等价关系,会进行对数式与指数式的互化. 3.理解常用对数、自然对数的概念及记法. 1.借助指数式与对数式的互化,培养逻辑推理素养.
2.应用对数的性质解题,培养数学运算素养.
(一)教材梳理填空
1.对数的概念:
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x= ,其中a叫做对数的 ,N叫做 .
logaN
底数
真数
2.常用对数与自然对数:
名称 定义 记法
常用对数 以____为底的对数叫做常用对数 _
自然对数 以无理数e=2.718 28…为底的对数称为自然对数 _
10
lg N
ln N
3.对数的基本性质:
(1)当a>0,且a≠1时,ax=N .
(2)负数和0没有对数.
(3)特殊值:1的对数是 ,即loga1= ;底数的对数是1,即logaa=1.
(4)如果把ax=N中的x写成logaN,则有alogaN=N.(对数恒等式)
[微思考] 在对数的定义中,为什么不能取a≤0及a=1呢?
x=logaN
0
0
2.若a2=M(a>0,且a≠1),则有 ( )
A.log2M=a B.logaM=2 C.loga2=M D.log2a=M
答案:B
3.若log2x=2,则x=__________.
答案:4
题型一 对数的概念
【学透用活】
(1)对数的概念的实质是指数式化为对数式,关键是弄清指数式各部分的“去向”:
(2)对数式y=logax有意义的条件是x>0,有时底数a>0,且a≠1也要考虑.
[方法技巧]
指数式与对数式互化的思路
(1)指数式化为对数式:将指数式的幂作为真数,指数作为对数,底数不变,写出对数式.
(2)对数式化为指数式:将对数式的真数作为幂,对数作为指数,底数不变,写出指数式.
[方法技巧]
利用指数与对数的互化求变量值的策略
(1)已知底数与指数,用指数式求幂.
(2)已知指数与幂,用指数式求底数.
(3)已知底数与幂,利用对数式表示指数.
题型三 对数的性质及对数恒等式
【学透用活】
[典例3] (1)求下列各式的值:
①2-log23;②e3ln 7;③lg 0.0012.
(2)求下列各式中x的值:
①log3(lg x)=1;②log3(log4(log5x))=0.
[方法技巧]
利用对数性质求解的两类问题的解法
(1)求多重对数式的值解题方法是由内到外,如求loga(logbc)的值,先求logbc的值,再求loga(logbc)的值.
(2)已知多重对数式的值,求变量值,应从外到内求,逐步脱去“log”后再求解.
2.[变设问]在本例(2)②条件下,计算625 log x3的值为________.
解析:因为x=625,则625 log 6253=3.
答案:3
3.[变条件]本例(2)②中若将“log3(log4(log5x))=0”改为“3log3(log4(log5x))=1”,则x=________.
解析:由3log3(log4(log5x))=1可得log4(log5x)=1,故log5x=4,所以x=54=625.
答案:625
【课堂思维激活】
一、综合性——强调融会贯通
1.某同学解等式“log(x-2)(x2-7x+13)=0中的x”,过程如下:
提示:不正确.忽略对数的底数a>0,且a≠1.
二、应用性——强调学以致用
2.分贝是计量声音强度相对大小的单位,物理学家引入了声压级来描述声音的大小;把声压p0=2×10-5帕作为参考声压.把所要测量的声压p与参考声压p0的比值取常用对数后乘20得到的数值成为声压级,声压级是听力学中最重要的参数之一,单位是分贝(dB),分贝值在60以下为无害区,60~110为过渡区,110以上为有害区.
(1)根据上述材料,列出分贝值y与声压p的函数关系式.
(2)某地声压p=0.002帕,试问:该地为以上所说的什么区?
(3)某电视台,现场录制节目时,现场多次响起响亮的掌声,某观众用仪器测量到最响亮的一次音量达到了90分贝,试求此时中央电视台演播大厅的声压是多少?
[析题建模]
三、创新性——强调创新意识和创新思维
3.对于任意实数x,符号[x]表示x的整数部分,即[x]是不超过x的最大整数.在实数轴R(箭头向右)上[x]是在点x左侧的第一个整数点,当x是整数时[x]就是x.这个函数[x]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用.求[lg 1]+[lg 2]+[lg 3]+…+[lg 10]+[lg 11]+[lg 12]+…+[lg 2 019]的值.
解:根据定义,[lg 1]=[lg 2]=[lg 3]=…[lg 9]=0;
[lg 10]=[lg 11]=[lg 12]=…[lg 99]=1;
[lg 100]=[lg 101]=[lg 102]=…=[lg 999]=2,
[lg 1 000]=[lg 1 001]=[lg 1 002]=…[lg 2 019]=3.
所以[lg 1]+[lg 2]+[lg 3]+…+[lg 10]+[lg 11]+[lg 12]+…+[lg 2 019]=1×(99-9)+2×(999-99)+3×(2 019-999)=90+2×900+3×1 020=4 950.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
