3.1.2 用树状图或表格求概率 课件(共29张PPT)
文档属性
| 名称 | 3.1.2 用树状图或表格求概率 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 801.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:42:26 | ||
图片预览





文档简介
(共29张PPT)
北师大版九年级上册
第三章
概率的进一步认识
3.1用树状图或表格求概率(二)
一、知识回顾
利用树状图或表格,我们可以不重复、不遗漏地列出所有可能性相同的结果,从而比较方便地求出某些事件发生的概率.
用画树状图和列表的方法求概率时,应注意各种结果出现的可能性务必相同.
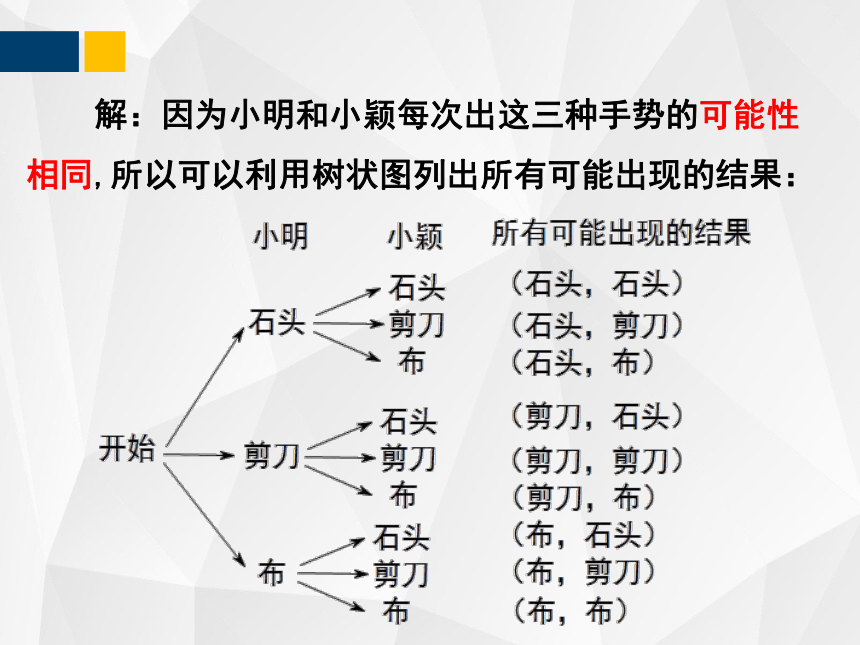
小明、小颖和小凡做“石头、剪刀、布”游戏.游戏规则如下:
由小明和小颖做“石头、剪刀、布”的游戏,如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者.
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?
二、探究新知
解:因为小明和小颖每次出这三种手势的可能性相同,所以可以利用树状图列出所有可能出现的结果:
总共有9种可能的结果,每种结果出现的可能性相同.
其中两人手势相同的结果有3种:(石头,石头)(剪刀,剪刀)(布,布),所以小凡获胜的概率为: ;
小明胜小颖的结果有3种:(石头,剪刀)(剪刀,布)(布,石头),所以小明获胜的概率为: ;
小颖胜小明的结果有3种:(剪刀,石头)(布,剪刀)(石头,布),所以小颖获胜的概率为: .
所以,这个游戏对三人是公平的.
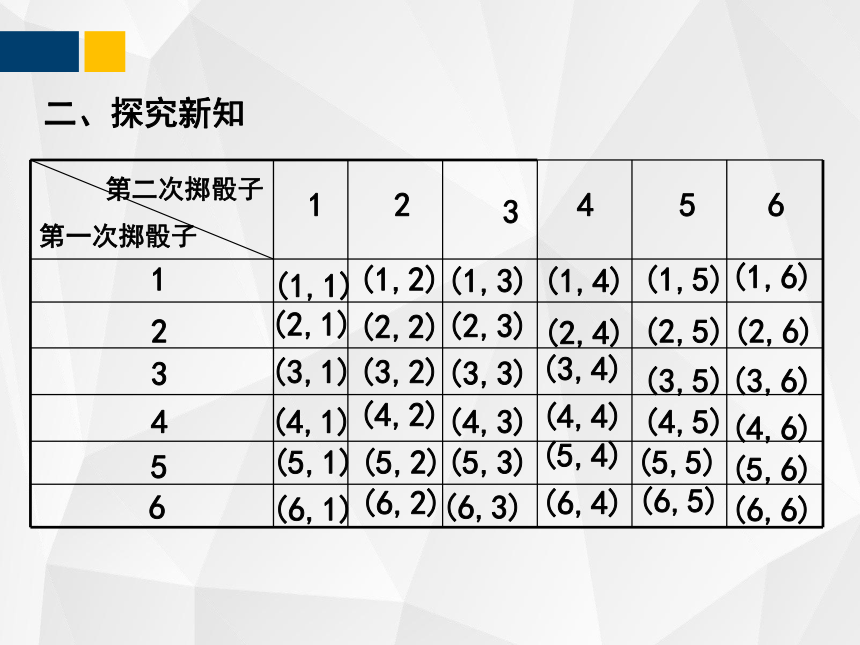
小明和小军两人一起做游戏.游戏规则如下:每人从1,2,…,12中任意选择一个数,然后两人各掷一次质地均匀的骰子,谁事先选择的数字等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负.如果你是游戏者,你会选择哪个数?
分析:这个问题看上去复杂,实际上,它等同于下面的问题:两人各掷一次均匀的骰子,将两人掷得的点数相加,点数为几的概率最大?
二、探究新知
第二次掷骰子 第一次掷骰子
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
3
(3,1)
(3,2)
4
4
6
5
(1,5)
(1,6)
(2,5)
(2,6)
(3,6)
(3,5)
(4,1)
(4,2)
(4,3)
(4,5)
(5,6)
(4,6)
(6,6)
(5,5)
(6,5)
(5,4)
(6,4)
(5,3)
(6,3)
(5,2)
(6,2)
(5,1)
(6,1)
5
6
(1,3)
(2,3)
(3,3)
(1,4)
(2,4)
(3,4)
(4,4)
二、探究新知
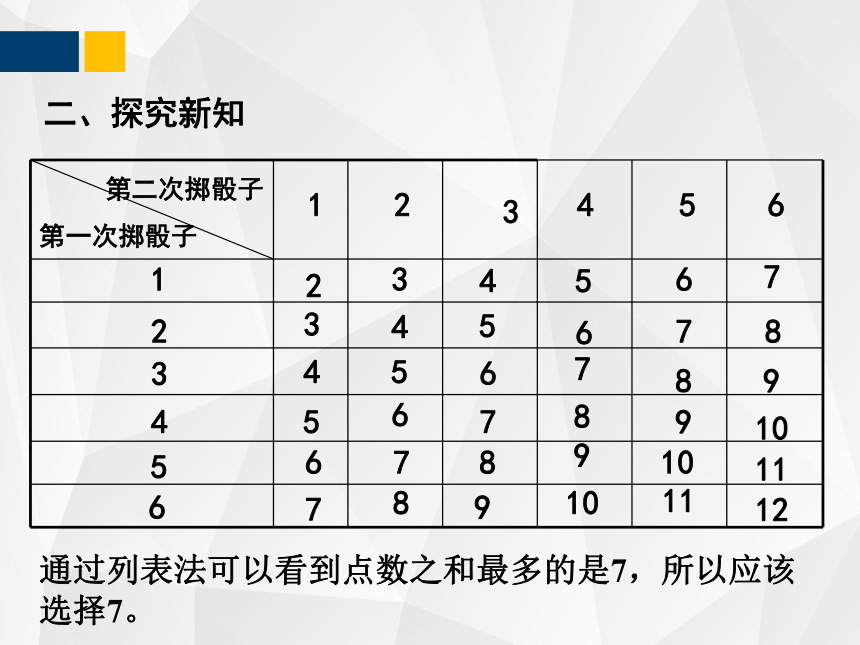
第二次掷骰子 第一次掷骰子
1
1
2
2
3
2
3
4
3
3
4
5
4
4
6
5
6
7
7
8
9
8
5
6
7
9
11
10
12
10
11
9
10
8
9
7
8
6
7
5
6
4
5
6
5
6
7
8
通过列表法可以看到点数之和最多的是7,所以应该选择7。
二、探究新知
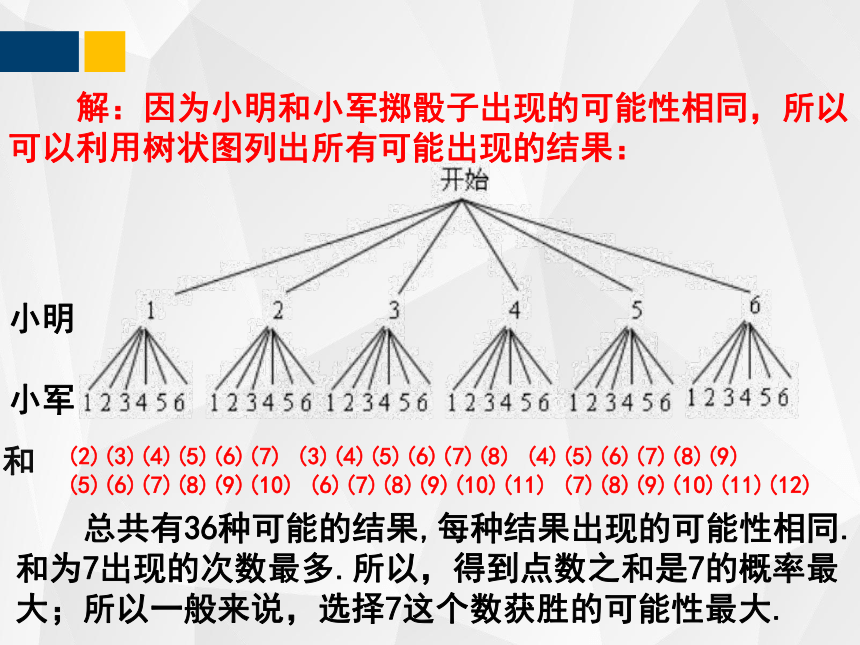
解:因为小明和小军掷骰子出现的可能性相同,所以可以利用树状图列出所有可能出现的结果:
小明
小军
和
(2)(3)(4)(5)(6)(7) (3)(4)(5)(6)(7)(8) (4)(5)(6)(7)(8)(9) (5)(6)(7)(8)(9)(10) (6)(7)(8)(9)(10)(11) (7)(8)(9)(10)(11)(12)
总共有36种可能的结果,每种结果出现的可能性相同.和为7出现的次数最多.所以,得到点数之和是7的概率最大;所以一般来说,选择7这个数获胜的可能性最大.
变式练习:
小可、子宣、欣怡三人在一起做游戏时,需要确定做游戏的先后顺序,她们约定用“石头、剪刀、布”的方式确定,那么在一个回合中,三个人都出“石头”的概率是多少?
二、探究新知
解:用树状图分析所有可能的结果,如图:
开始
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
...... ...... ...... ......
由树状图可知所有等可能的结果有27种,三人都出“石头”的结果只有1种,所以在一个回合中三个人都出“石头”的概率为 .
总结归纳:
当一次试验涉及两个因素时,用列表法较简便;当一次试验涉及3个或更多的因素时,用画树状图法较简便
解:画树状图如下:
共有6种情况,两次摸到不同颜色球的有4种,
∴P(两次摸到不同颜色的球)= =
一只箱子里共有3个球,其中有2个黑球,1个白球,它们除了颜色外均相同,从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出不同颜色球的概率;
三、典例讲解
1
2
黑1 黑2 白
黑1 —— (黑2,黑1) (白,黑1)
黑2 (黑1,黑2) —— (白,黑2)
白 (黑1,白) (黑2,白) ——
解:列表如下:
第二次
第一次
共有6种情况,两次摸到不同颜色球的有4种,
∴P(两次摸到不同颜色的球)= =
2.将正面分别标有数字6,7,8,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上,一次性抽出两张卡片,恰好都是偶数的概率是多少?
三、典例讲解
三、典例讲解
6 7 8
6 —— (6,7) (6,8)
7 (7,6) —— (7,8)
8 (8,6) (8,7) ——
解:列表如下:
第一次
第二次
共有6种情况,两次都是偶数有2种,
∴P(一次性抽出两张卡片都是偶数)= =
在求概率时要正确区分“放回”和“不放回”事件.
总结归纳:
1.从长度分别为1,3,5,7的四条线段中任选三条作边,能构成三角形的概率为( )
A. B. C. D.
C
四、课堂练习
2.某校举行“激情五月,唱响青春”为主题的演讲比赛,决赛阶段只剩下甲、乙、丙、丁四名同学,则甲、乙同学获得前两名的概率是( )
四、课堂练习
D
3.在一个不透明的袋中装有2个黄球和2个红球,它们除颜色外没有其他区别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸一个球,那么两次都摸到黄球的概率是 ( )
A. B. C. D.
C
四、课堂练习
4.袋中装有大小一样的白球和黑球各3个,从中任取2个球,则两个均为黑球的概率是( )
四、课堂练习
D
5.一个袋中有2个红球,2个黄球,每个球除颜色外都相同,从中一次摸出2个球,2个球都是红球的可能性是( )
A. B. C. D.
D
四、课堂练习
四、课堂练习
6.小雷有某文学名著上、中、下各1册,她随机将它们叠放在一起,从上到下的顺序恰好为“上册、中册、下册”的概率 。
7.一个布袋里装有4个大小、质地均匀相同的乒乓球,每个球上面分别标有1,2,3,4,先从布袋中随机抽取一个球(不放回),再随机抽取第二个球.
(1)请你列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
解:(1)画树状图如下:
共有12种情况.
(2)积有2,3,4,2,6,8,3,6,12,4,8,12,
P(两次取得乒乓球的数字之积为奇数)= =
8.把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上数字1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中各随机投取一张.
(1)试求取出的两张卡片数字之和为奇数概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
解:(1)用树状图列出所有的可能情形如下:
共有9种等可能事件,和为偶数有4种,所以
(2)由于
所以这个游戏不公平.
五、课堂小结
当一次试验涉及两个因素时,用列表法较简便;当一次试验涉及3个或更多的因素时,用画树状图法较简便
在求概率时要正确区分“放回”和“不放回”事件.
六、布置作业
课本P64 习题3.2 第1,2,3,4题
谢谢聆听
北师大版九年级上册
第三章
概率的进一步认识
3.1用树状图或表格求概率(二)
一、知识回顾
利用树状图或表格,我们可以不重复、不遗漏地列出所有可能性相同的结果,从而比较方便地求出某些事件发生的概率.
用画树状图和列表的方法求概率时,应注意各种结果出现的可能性务必相同.
小明、小颖和小凡做“石头、剪刀、布”游戏.游戏规则如下:
由小明和小颖做“石头、剪刀、布”的游戏,如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者.
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?
二、探究新知
解:因为小明和小颖每次出这三种手势的可能性相同,所以可以利用树状图列出所有可能出现的结果:
总共有9种可能的结果,每种结果出现的可能性相同.
其中两人手势相同的结果有3种:(石头,石头)(剪刀,剪刀)(布,布),所以小凡获胜的概率为: ;
小明胜小颖的结果有3种:(石头,剪刀)(剪刀,布)(布,石头),所以小明获胜的概率为: ;
小颖胜小明的结果有3种:(剪刀,石头)(布,剪刀)(石头,布),所以小颖获胜的概率为: .
所以,这个游戏对三人是公平的.
小明和小军两人一起做游戏.游戏规则如下:每人从1,2,…,12中任意选择一个数,然后两人各掷一次质地均匀的骰子,谁事先选择的数字等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负.如果你是游戏者,你会选择哪个数?
分析:这个问题看上去复杂,实际上,它等同于下面的问题:两人各掷一次均匀的骰子,将两人掷得的点数相加,点数为几的概率最大?
二、探究新知
第二次掷骰子 第一次掷骰子
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
3
(3,1)
(3,2)
4
4
6
5
(1,5)
(1,6)
(2,5)
(2,6)
(3,6)
(3,5)
(4,1)
(4,2)
(4,3)
(4,5)
(5,6)
(4,6)
(6,6)
(5,5)
(6,5)
(5,4)
(6,4)
(5,3)
(6,3)
(5,2)
(6,2)
(5,1)
(6,1)
5
6
(1,3)
(2,3)
(3,3)
(1,4)
(2,4)
(3,4)
(4,4)
二、探究新知
第二次掷骰子 第一次掷骰子
1
1
2
2
3
2
3
4
3
3
4
5
4
4
6
5
6
7
7
8
9
8
5
6
7
9
11
10
12
10
11
9
10
8
9
7
8
6
7
5
6
4
5
6
5
6
7
8
通过列表法可以看到点数之和最多的是7,所以应该选择7。
二、探究新知
解:因为小明和小军掷骰子出现的可能性相同,所以可以利用树状图列出所有可能出现的结果:
小明
小军
和
(2)(3)(4)(5)(6)(7) (3)(4)(5)(6)(7)(8) (4)(5)(6)(7)(8)(9) (5)(6)(7)(8)(9)(10) (6)(7)(8)(9)(10)(11) (7)(8)(9)(10)(11)(12)
总共有36种可能的结果,每种结果出现的可能性相同.和为7出现的次数最多.所以,得到点数之和是7的概率最大;所以一般来说,选择7这个数获胜的可能性最大.
变式练习:
小可、子宣、欣怡三人在一起做游戏时,需要确定做游戏的先后顺序,她们约定用“石头、剪刀、布”的方式确定,那么在一个回合中,三个人都出“石头”的概率是多少?
二、探究新知
解:用树状图分析所有可能的结果,如图:
开始
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
...... ...... ...... ......
由树状图可知所有等可能的结果有27种,三人都出“石头”的结果只有1种,所以在一个回合中三个人都出“石头”的概率为 .
总结归纳:
当一次试验涉及两个因素时,用列表法较简便;当一次试验涉及3个或更多的因素时,用画树状图法较简便
解:画树状图如下:
共有6种情况,两次摸到不同颜色球的有4种,
∴P(两次摸到不同颜色的球)= =
一只箱子里共有3个球,其中有2个黑球,1个白球,它们除了颜色外均相同,从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出不同颜色球的概率;
三、典例讲解
1
2
黑1 黑2 白
黑1 —— (黑2,黑1) (白,黑1)
黑2 (黑1,黑2) —— (白,黑2)
白 (黑1,白) (黑2,白) ——
解:列表如下:
第二次
第一次
共有6种情况,两次摸到不同颜色球的有4种,
∴P(两次摸到不同颜色的球)= =
2.将正面分别标有数字6,7,8,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上,一次性抽出两张卡片,恰好都是偶数的概率是多少?
三、典例讲解
三、典例讲解
6 7 8
6 —— (6,7) (6,8)
7 (7,6) —— (7,8)
8 (8,6) (8,7) ——
解:列表如下:
第一次
第二次
共有6种情况,两次都是偶数有2种,
∴P(一次性抽出两张卡片都是偶数)= =
在求概率时要正确区分“放回”和“不放回”事件.
总结归纳:
1.从长度分别为1,3,5,7的四条线段中任选三条作边,能构成三角形的概率为( )
A. B. C. D.
C
四、课堂练习
2.某校举行“激情五月,唱响青春”为主题的演讲比赛,决赛阶段只剩下甲、乙、丙、丁四名同学,则甲、乙同学获得前两名的概率是( )
四、课堂练习
D
3.在一个不透明的袋中装有2个黄球和2个红球,它们除颜色外没有其他区别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸一个球,那么两次都摸到黄球的概率是 ( )
A. B. C. D.
C
四、课堂练习
4.袋中装有大小一样的白球和黑球各3个,从中任取2个球,则两个均为黑球的概率是( )
四、课堂练习
D
5.一个袋中有2个红球,2个黄球,每个球除颜色外都相同,从中一次摸出2个球,2个球都是红球的可能性是( )
A. B. C. D.
D
四、课堂练习
四、课堂练习
6.小雷有某文学名著上、中、下各1册,她随机将它们叠放在一起,从上到下的顺序恰好为“上册、中册、下册”的概率 。
7.一个布袋里装有4个大小、质地均匀相同的乒乓球,每个球上面分别标有1,2,3,4,先从布袋中随机抽取一个球(不放回),再随机抽取第二个球.
(1)请你列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
解:(1)画树状图如下:
共有12种情况.
(2)积有2,3,4,2,6,8,3,6,12,4,8,12,
P(两次取得乒乓球的数字之积为奇数)= =
8.把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上数字1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中各随机投取一张.
(1)试求取出的两张卡片数字之和为奇数概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
解:(1)用树状图列出所有的可能情形如下:
共有9种等可能事件,和为偶数有4种,所以
(2)由于
所以这个游戏不公平.
五、课堂小结
当一次试验涉及两个因素时,用列表法较简便;当一次试验涉及3个或更多的因素时,用画树状图法较简便
在求概率时要正确区分“放回”和“不放回”事件.
六、布置作业
课本P64 习题3.2 第1,2,3,4题
谢谢聆听
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
