3.2 用频率估计概率 课件(共25张PPT)
文档属性
| 名称 | 3.2 用频率估计概率 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 669.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:40:16 | ||
图片预览








文档简介
(共25张PPT)
北师大版九年级上册
第三章
概率的进一步认识
3.2 用频率估计概率
频数:在实验中,每个对象出现的次数称为频数,
概率:事件发生的可能性,也称为事件发生的概率.
频率=
A可能发生的情况
可能发生的总情况
频率:所考察对象出现的次数与实验的总次数的比叫做频率
一、知识回顾
(1) 400个同学中,一定有2人的生日相同(可以不同年)吗?
(2) 300个同学中,一定有2人的生日相同吗?
(3)“ 50个同学中,有可能有2人的生日相同”你同意这个说法吗?
二、探究新知
思考下列问题:
活动探究:
50个同学中,有2人的生日相同的概率
方案:我们可以通过大量重复试验,用“50个人中有2个人的生日相同”的频率来估计这一事件的概率。
对于一些比较复杂的或不能计算出概率的事件,可以通过大量重复试验,当试验次数越多时,频率越稳定于概率,然后用频率来估计概率.
(3)根据表格中数据,“估计50个人中有2个人的生日相同”的概率.
实验总次数 50 100 150 200 250 …
“有2个生日相同”次数
“有2个生日相同”频率
(1)每天同学课外调查10个人的生日
(2)从全班的调查结果中随机选取50个调查人的生日,记录其中有无2个人的生日相同,每选取50个被调查人的生日为一次试验,重复尽可能多次试验
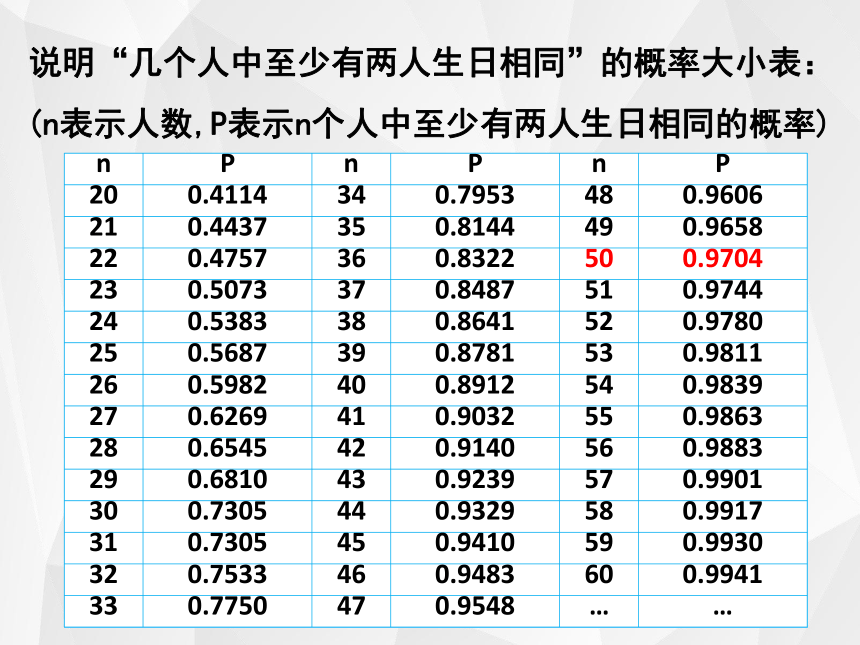
说明“几个人中至少有两人生日相同”的概率大小表:
(n表示人数,P表示n个人中至少有两人生日相同的概率)
n P n P n P
20 0.4114 34 0.7953 48 0.9606
21 0.4437 35 0.8144 49 0.9658
22 0.4757 36 0.8322 50 0.9704
23 0.5073 37 0.8487 51 0.9744
24 0.5383 38 0.8641 52 0.9780
25 0.5687 39 0.8781 53 0.9811
26 0.5982 40 0.8912 54 0.9839
27 0.6269 41 0.9032 55 0.9863
28 0.6545 42 0.9140 56 0.9883
29 0.6810 43 0.9239 57 0.9901
30 0.7305 44 0.9329 58 0.9917
31 0.7305 45 0.9410 59 0.9930
32 0.7533 46 0.9483 60 0.9941
33 0.7750 47 0.9548 … …
数学史实
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.这称为大数法则,亦称大数定律.
由频率可以估计概率是由瑞士数学家雅各布·伯努利(1654-1705)最早阐明的,因而他被公认为是概率论的先驱之一.
频率稳定性定理
联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率;
区别:某可能事件发生的概率是一个定值.而这一事件发生的频率是波动的,当试验次数不大时,事件发生的频率与概率的差异很大,要通过大量重复试验,才能用事件发生频率来估计的概率.
应用:试验频率≈理论概率.
试验频率与理论概率之间的关系
(1)当试验的可能结果发生的可能性相等时,且是很容易计算时,利用概率公式P(A)= 的方式得出概率.
(2)当试验的所有可能结果发生的可能性不相等时,或者可能结果发生的可能性相等但不好计算时,通过大量重复试验所得到的随机事件发生的频率来估计概率
总结归纳:
1.姚明在某段时间内进行定点投篮训练,其成绩如下:
试估计姚明在这段时间内定点投篮投中的概率是
_______(精确到0.1).
投篮次数 10 100 10 000
投中次数 9 89 9 012
0.9
三、典例讲解
三、典例讲解
2.在一个不透明的口袋中装有5个白球,若干个黑球,它们除颜色外其他完全相同,经过多次实验发现摸到白球的频率稳定在0.2附近,则黑球大约有________个.
20
3.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
三、典例讲解
(1)当n很大时,摸到白球的概率约为_____(精确到0.1)
(2)估算盒子里有白球________个;
0.6
24
三、典例讲解
(3)若向盒子里再放入x个除颜色以外其他完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是________.
三、典例讲解
(3)若向盒子里再放入x个除颜色以外其他完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是________.
三、典例讲解
1. 从生产的一批螺钉中抽取1 000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品的概率为( )
A. B. C. D.
B
四、课堂练习
2.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是 ( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
四、课堂练习
C
3.小亮是一名职业足球队员,根据以往比赛数据统计,小亮进球率为10%,他明天将参加一场比赛,下面几种说法正确的是( )
A.小亮明天的进球率为10%
B.小亮明天每射球10次必进球1次
C.小亮明天有可能进球
D.小亮明天肯定进球
四、课堂练习
4.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
0.8 B. 0.9 C. 0.95 D. 1
C
四、课堂练习
5. 在一个不透明的盒子中装有a个除颜色外完全相同的球,这a个球中只有3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为( )
A.12 B.15 C.18 D.21
B
四、课堂练习
6. 在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟试验次数与摸出黑球次数的列表:
根据列表,可以估计出n的值是________.
摸球试验次数 100 1 000 5000 10 000 50 000 100 000
摸出黑球次数 46 487 2 506 5 008 24 996 50 007
10
四、课堂练习
摸球的次数n 100 300 500 800 1 000
摸到白球的次数m 65 178 302 481 599
摸到白球的频率 0.65 0.593 0.604 0.601 0.599
7. 在一个不透明的盒子里装有黑、白两种球共40个,小颖做摸球实验,她从中随机摸出一个球记下颜色放回,不断重复上述过程,下表是实验中的统计数据:
(1)当n很大时,摸到白球的频率将会接近________;(精确到0.1)
(2)若你摸一次,你摸到白球的概率P(白球)=________;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
0.6
0.6
五、课堂小结
用频率估计概率:试验频率≈理论概率.
频率与概率的关系
当试验次数很多或试验时样本容量足够大时,一件事件发生的频率稳定于概率,此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
六、布置作业
课本P71 习题3.4 第1题
谢谢聆听
北师大版九年级上册
第三章
概率的进一步认识
3.2 用频率估计概率
频数:在实验中,每个对象出现的次数称为频数,
概率:事件发生的可能性,也称为事件发生的概率.
频率=
A可能发生的情况
可能发生的总情况
频率:所考察对象出现的次数与实验的总次数的比叫做频率
一、知识回顾
(1) 400个同学中,一定有2人的生日相同(可以不同年)吗?
(2) 300个同学中,一定有2人的生日相同吗?
(3)“ 50个同学中,有可能有2人的生日相同”你同意这个说法吗?
二、探究新知
思考下列问题:
活动探究:
50个同学中,有2人的生日相同的概率
方案:我们可以通过大量重复试验,用“50个人中有2个人的生日相同”的频率来估计这一事件的概率。
对于一些比较复杂的或不能计算出概率的事件,可以通过大量重复试验,当试验次数越多时,频率越稳定于概率,然后用频率来估计概率.
(3)根据表格中数据,“估计50个人中有2个人的生日相同”的概率.
实验总次数 50 100 150 200 250 …
“有2个生日相同”次数
“有2个生日相同”频率
(1)每天同学课外调查10个人的生日
(2)从全班的调查结果中随机选取50个调查人的生日,记录其中有无2个人的生日相同,每选取50个被调查人的生日为一次试验,重复尽可能多次试验
说明“几个人中至少有两人生日相同”的概率大小表:
(n表示人数,P表示n个人中至少有两人生日相同的概率)
n P n P n P
20 0.4114 34 0.7953 48 0.9606
21 0.4437 35 0.8144 49 0.9658
22 0.4757 36 0.8322 50 0.9704
23 0.5073 37 0.8487 51 0.9744
24 0.5383 38 0.8641 52 0.9780
25 0.5687 39 0.8781 53 0.9811
26 0.5982 40 0.8912 54 0.9839
27 0.6269 41 0.9032 55 0.9863
28 0.6545 42 0.9140 56 0.9883
29 0.6810 43 0.9239 57 0.9901
30 0.7305 44 0.9329 58 0.9917
31 0.7305 45 0.9410 59 0.9930
32 0.7533 46 0.9483 60 0.9941
33 0.7750 47 0.9548 … …
数学史实
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.这称为大数法则,亦称大数定律.
由频率可以估计概率是由瑞士数学家雅各布·伯努利(1654-1705)最早阐明的,因而他被公认为是概率论的先驱之一.
频率稳定性定理
联系:当试验次数很大时,事件发生的频率稳定在相应概率的附近,即试验频率稳定于理论概率;
区别:某可能事件发生的概率是一个定值.而这一事件发生的频率是波动的,当试验次数不大时,事件发生的频率与概率的差异很大,要通过大量重复试验,才能用事件发生频率来估计的概率.
应用:试验频率≈理论概率.
试验频率与理论概率之间的关系
(1)当试验的可能结果发生的可能性相等时,且是很容易计算时,利用概率公式P(A)= 的方式得出概率.
(2)当试验的所有可能结果发生的可能性不相等时,或者可能结果发生的可能性相等但不好计算时,通过大量重复试验所得到的随机事件发生的频率来估计概率
总结归纳:
1.姚明在某段时间内进行定点投篮训练,其成绩如下:
试估计姚明在这段时间内定点投篮投中的概率是
_______(精确到0.1).
投篮次数 10 100 10 000
投中次数 9 89 9 012
0.9
三、典例讲解
三、典例讲解
2.在一个不透明的口袋中装有5个白球,若干个黑球,它们除颜色外其他完全相同,经过多次实验发现摸到白球的频率稳定在0.2附近,则黑球大约有________个.
20
3.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
三、典例讲解
(1)当n很大时,摸到白球的概率约为_____(精确到0.1)
(2)估算盒子里有白球________个;
0.6
24
三、典例讲解
(3)若向盒子里再放入x个除颜色以外其他完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是________.
三、典例讲解
(3)若向盒子里再放入x个除颜色以外其他完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是________.
三、典例讲解
1. 从生产的一批螺钉中抽取1 000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品的概率为( )
A. B. C. D.
B
四、课堂练习
2.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是 ( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
四、课堂练习
C
3.小亮是一名职业足球队员,根据以往比赛数据统计,小亮进球率为10%,他明天将参加一场比赛,下面几种说法正确的是( )
A.小亮明天的进球率为10%
B.小亮明天每射球10次必进球1次
C.小亮明天有可能进球
D.小亮明天肯定进球
四、课堂练习
4.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
0.8 B. 0.9 C. 0.95 D. 1
C
四、课堂练习
5. 在一个不透明的盒子中装有a个除颜色外完全相同的球,这a个球中只有3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为( )
A.12 B.15 C.18 D.21
B
四、课堂练习
6. 在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟试验次数与摸出黑球次数的列表:
根据列表,可以估计出n的值是________.
摸球试验次数 100 1 000 5000 10 000 50 000 100 000
摸出黑球次数 46 487 2 506 5 008 24 996 50 007
10
四、课堂练习
摸球的次数n 100 300 500 800 1 000
摸到白球的次数m 65 178 302 481 599
摸到白球的频率 0.65 0.593 0.604 0.601 0.599
7. 在一个不透明的盒子里装有黑、白两种球共40个,小颖做摸球实验,她从中随机摸出一个球记下颜色放回,不断重复上述过程,下表是实验中的统计数据:
(1)当n很大时,摸到白球的频率将会接近________;(精确到0.1)
(2)若你摸一次,你摸到白球的概率P(白球)=________;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
0.6
0.6
五、课堂小结
用频率估计概率:试验频率≈理论概率.
频率与概率的关系
当试验次数很多或试验时样本容量足够大时,一件事件发生的频率稳定于概率,此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
六、布置作业
课本P71 习题3.4 第1题
谢谢聆听
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
