1.1空间向量及其运算-1.1.2空间向量的数量积运算 课件(共27页)
文档属性
| 名称 | 1.1空间向量及其运算-1.1.2空间向量的数量积运算 课件(共27页) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:26:06 | ||
图片预览






文档简介
(共27张PPT)
1.1
空间向量及其运算
第一章
1.1.2 空间向量的数量积运算
学习目标
1.会识别空间向量的夹角.
2.掌握空间向量的数量积的定义、性质、运算律及计算方法.
3.能用空间向量数量积解决简单的立体几何问题.
核心素养:数学运算、逻辑推理、直观想象
新知讲解
一 空间向量的夹角
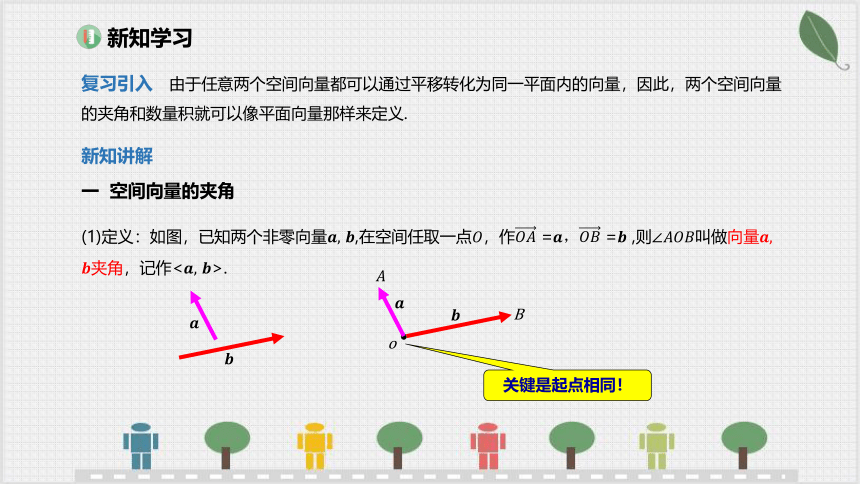
(1)定义:如图,已知两个非零向量 ,在空间任取一点,作 = = ,则∠叫做向量 夹角,记作< >.
o
B
关键是起点相同!
复习引入 由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
新知学习
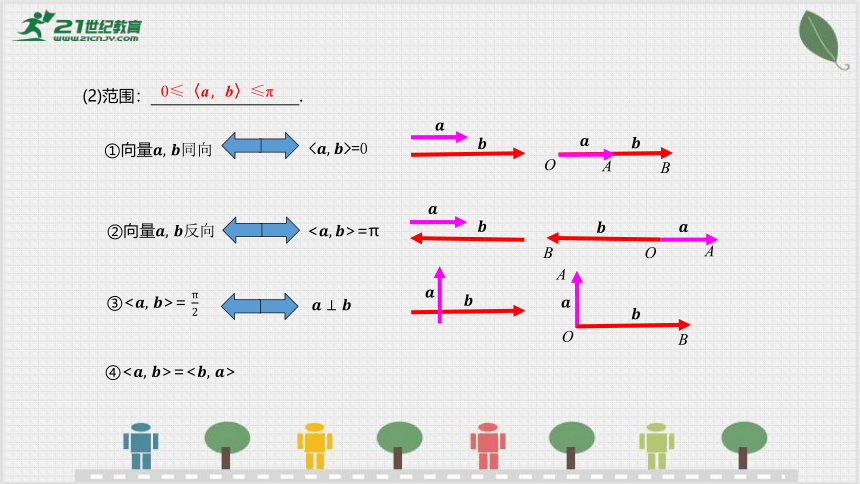
(2)范围: .
0≤〈a,b〉≤π
①向量
O
A
B
< >=0
A
B
O
A
B
<>=π
③< >=
④< >=< >
②向量
O
二 两个向量的数量积
(1)定义:已知两个非零向量 ,则 ||cos< >叫做 的数量积,记作.
即= ||cos< >.
注意:①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于0.即=0.
(2) 性质
两个向量数量积的性质 ①若,是非零向量,则⊥ _______.
②若与同向,则·=______;若反向,则·=________.
③特别地,·=____或||=__ _.
④若〈,〉为,的夹角,则cos〈,〉=_______.
⑤|·|≤||·||
a·b=0
|a|·|b|
-|a|·|b|
|a|2
(判断向量垂直)
(向量的模长公式)
(向量的夹角公式)
三 空间向量数量积运算律
向量数量积的运算不满足消去律、作商和乘法的结合律 ,即= =,= ,都不成立.
(1)=
(2)()·=
(3) ·(+)=
() =·()
+
(交换律)
(分配律)
思考 对应向量成立吗
(数乘结合律)
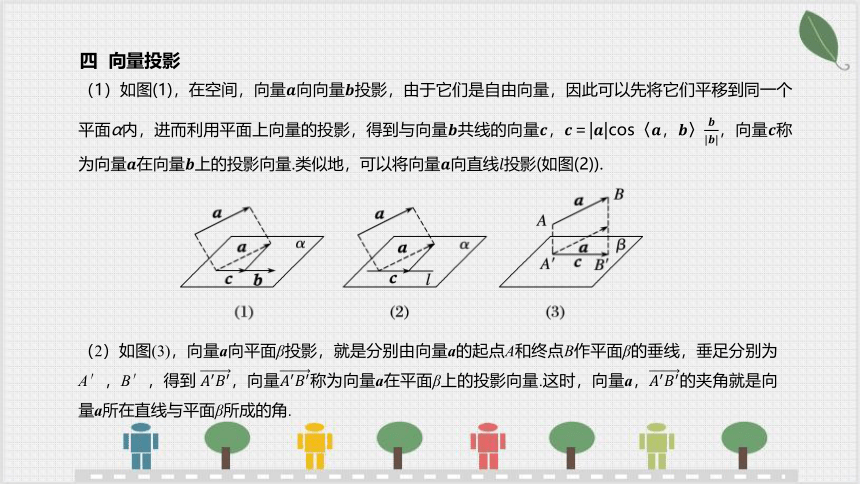
(1)如图(1),在空间,向量向向量投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量共线的向量,=||cos〈,〉,向量称为向量在向量上的投影向量.类似地,可以将向量向直线投影(如图(2)).
四 向量投影
(2)如图(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到 ,向量称为向量a在平面β上的投影向量.这时,向量a,的夹角就是向量a所在直线与平面β所成的角.
即时巩固
2.若=0,则=0或=0.( )
3.对于非零向量,由=,可得.( )
4.若非零向量,为共线且同向的向量,则=||||.( )
×
√
×
√
一、数量积的计算
例1 如图所示,在棱长为1的正四面体中,,分别是,的中点,求:
典例剖析
=cos 60°-cos 60°=0.
反思感悟 求空间向量数量积的步骤
(1)将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入=求解.
跟踪训练 (1)已知a=3p-2q,b=p+q,p和q是相互垂直的单位向量,则a·b等于( )
A.1 B.2 C.3 D.4
A
解析 ∵且
∴
=3+0-2=1.
2
=4-0+0-2=2.
二、利用数量积证明垂直问题
例2 如图所示,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,求证:A1O⊥平面GBD.
则a·b=0,b·c=0,a·c=0,|a|=|b|=|c|.
又∵OG∩BD=O,OG 平面GBD,BD 平面GBD,∴A1O⊥平面GBD.
反思感悟
反思感悟 用向量法证明几何中垂直关系问题的思路
(1)要证两直线垂直,可分别构造与两直线平行的向量,只要证明这两个向量的数量积为0即可.
(2)用向量法证明线面垂直,需将线面垂直转化为线线垂直,然后利用向量数量积证明线线垂直即可.
跟踪训练 如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.求证:PA⊥BD.
证明 在△ADB中,∠DAB=60°,AB=2AD,
所以AD2+BD2=AB2,
三、用数量积求解夹角和模
例3 如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,点N为AA1的中点.
延伸探究
2.(变条件)本例中,若CA=CB=AA1=1,其他条件不变,求异面直线CA1与AB的夹角.
所以异面直线CA1与AB的夹角为60°.
反思感悟 求向量的夹角和模
(1)求两个向量的夹角:利用公式cos〈a,b〉= 求cos〈a,b〉,进而确定〈a,b〉.
(2)求线段长度(距离):①取此线段对应的向量; ②用其他已知夹角和模的向量表示该向量;③利用|a|= ,计算出|a|,即得所求长度(距离).
A.30° B.60° C.90° D.120°
D
跟踪训练
1.如图所示,在正方体ABCD-A1B1C1D1中,下列各组向量的夹角为45°的是( )
A
随堂小测
2.设ABCD-A1B1C1D1是棱长为a的正方体,则有( )
C
D
4.若a,b,c为空间两两夹角都是60°的三个单位向量,则|a-b+2c|=_____.
解析 |a-b+2c|2=(a-b+2c)2=a2+b2+4c2-2a·b+4a·c-4b·c=5.
60°
1
即△PA1D为等边三角形,从而∠PA1D=60°,
方法二 根据向量的线性运算可得
7.如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=7,AC=BD=24,线段BD与α所成的角为30°,求CD的长.
解 由AC⊥α,可知AC⊥AB,过点D作DD1⊥α,
D1为垂足,连接BD1,则∠DBD1为BD与α所成的角,
即∠DBD1=30°,所以∠BDD1=60°,
因为AC⊥α,DD1⊥α,所以AC∥DD1,
因为BD⊥AB,AC⊥AB,
=242+72+242+2×24×24×cos 120°=625,
1.知识清单:
(1)空间向量的夹角、投影.
(2)空间向量数量积、性质及运算律.
2.方法归纳:化归转化.
3.常见误区:空间向量的数量积的注意点
(1)数量积的符号由夹角的余弦值决定.
(2)当a≠0,由a·b=0可得a⊥b或b=0.
课堂小结
谢 谢!
1.1
空间向量及其运算
第一章
1.1.2 空间向量的数量积运算
学习目标
1.会识别空间向量的夹角.
2.掌握空间向量的数量积的定义、性质、运算律及计算方法.
3.能用空间向量数量积解决简单的立体几何问题.
核心素养:数学运算、逻辑推理、直观想象
新知讲解
一 空间向量的夹角
(1)定义:如图,已知两个非零向量 ,在空间任取一点,作 = = ,则∠叫做向量 夹角,记作< >.
o
B
关键是起点相同!
复习引入 由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
新知学习
(2)范围: .
0≤〈a,b〉≤π
①向量
O
A
B
< >=0
A
B
O
A
B
<>=π
③< >=
④< >=< >
②向量
O
二 两个向量的数量积
(1)定义:已知两个非零向量 ,则 ||cos< >叫做 的数量积,记作.
即= ||cos< >.
注意:①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于0.即=0.
(2) 性质
两个向量数量积的性质 ①若,是非零向量,则⊥ _______.
②若与同向,则·=______;若反向,则·=________.
③特别地,·=____或||=__ _.
④若〈,〉为,的夹角,则cos〈,〉=_______.
⑤|·|≤||·||
a·b=0
|a|·|b|
-|a|·|b|
|a|2
(判断向量垂直)
(向量的模长公式)
(向量的夹角公式)
三 空间向量数量积运算律
向量数量积的运算不满足消去律、作商和乘法的结合律 ,即= =,= ,都不成立.
(1)=
(2)()·=
(3) ·(+)=
() =·()
+
(交换律)
(分配律)
思考 对应向量成立吗
(数乘结合律)
(1)如图(1),在空间,向量向向量投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量共线的向量,=||cos〈,〉,向量称为向量在向量上的投影向量.类似地,可以将向量向直线投影(如图(2)).
四 向量投影
(2)如图(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到 ,向量称为向量a在平面β上的投影向量.这时,向量a,的夹角就是向量a所在直线与平面β所成的角.
即时巩固
2.若=0,则=0或=0.( )
3.对于非零向量,由=,可得.( )
4.若非零向量,为共线且同向的向量,则=||||.( )
×
√
×
√
一、数量积的计算
例1 如图所示,在棱长为1的正四面体中,,分别是,的中点,求:
典例剖析
=cos 60°-cos 60°=0.
反思感悟 求空间向量数量积的步骤
(1)将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入=求解.
跟踪训练 (1)已知a=3p-2q,b=p+q,p和q是相互垂直的单位向量,则a·b等于( )
A.1 B.2 C.3 D.4
A
解析 ∵且
∴
=3+0-2=1.
2
=4-0+0-2=2.
二、利用数量积证明垂直问题
例2 如图所示,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,求证:A1O⊥平面GBD.
则a·b=0,b·c=0,a·c=0,|a|=|b|=|c|.
又∵OG∩BD=O,OG 平面GBD,BD 平面GBD,∴A1O⊥平面GBD.
反思感悟
反思感悟 用向量法证明几何中垂直关系问题的思路
(1)要证两直线垂直,可分别构造与两直线平行的向量,只要证明这两个向量的数量积为0即可.
(2)用向量法证明线面垂直,需将线面垂直转化为线线垂直,然后利用向量数量积证明线线垂直即可.
跟踪训练 如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.求证:PA⊥BD.
证明 在△ADB中,∠DAB=60°,AB=2AD,
所以AD2+BD2=AB2,
三、用数量积求解夹角和模
例3 如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,点N为AA1的中点.
延伸探究
2.(变条件)本例中,若CA=CB=AA1=1,其他条件不变,求异面直线CA1与AB的夹角.
所以异面直线CA1与AB的夹角为60°.
反思感悟 求向量的夹角和模
(1)求两个向量的夹角:利用公式cos〈a,b〉= 求cos〈a,b〉,进而确定〈a,b〉.
(2)求线段长度(距离):①取此线段对应的向量; ②用其他已知夹角和模的向量表示该向量;③利用|a|= ,计算出|a|,即得所求长度(距离).
A.30° B.60° C.90° D.120°
D
跟踪训练
1.如图所示,在正方体ABCD-A1B1C1D1中,下列各组向量的夹角为45°的是( )
A
随堂小测
2.设ABCD-A1B1C1D1是棱长为a的正方体,则有( )
C
D
4.若a,b,c为空间两两夹角都是60°的三个单位向量,则|a-b+2c|=_____.
解析 |a-b+2c|2=(a-b+2c)2=a2+b2+4c2-2a·b+4a·c-4b·c=5.
60°
1
即△PA1D为等边三角形,从而∠PA1D=60°,
方法二 根据向量的线性运算可得
7.如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=7,AC=BD=24,线段BD与α所成的角为30°,求CD的长.
解 由AC⊥α,可知AC⊥AB,过点D作DD1⊥α,
D1为垂足,连接BD1,则∠DBD1为BD与α所成的角,
即∠DBD1=30°,所以∠BDD1=60°,
因为AC⊥α,DD1⊥α,所以AC∥DD1,
因为BD⊥AB,AC⊥AB,
=242+72+242+2×24×24×cos 120°=625,
1.知识清单:
(1)空间向量的夹角、投影.
(2)空间向量数量积、性质及运算律.
2.方法归纳:化归转化.
3.常见误区:空间向量的数量积的注意点
(1)数量积的符号由夹角的余弦值决定.
(2)当a≠0,由a·b=0可得a⊥b或b=0.
课堂小结
谢 谢!
