2.2.1直线的点斜式方程 课件(共19页)
文档属性
| 名称 | 2.2.1直线的点斜式方程 课件(共19页) |  | |
| 格式 | pptx | ||
| 文件大小 | 812.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:26:06 | ||
图片预览





文档简介
(共19张PPT)
2.2.1 直线的点斜式方程
第二章
2.2
直线的方程
学习目标
1.掌握直线方程的点斜式和斜截式,并会用它们求直线的方程.
2.了解直线的斜截式方程与一次函数的关系.
3. 会用直线的点斜式方程与斜截式方程解决直线的平行与垂直问题.
核心素养:数学抽象、数学运算、逻辑推理
1.直线的斜率公式
注意:不是所有的直线都有斜率,
斜率不存在的直线为与轴垂直的直线.
新知学习
链接回顾
(1)tan
(2)( )
2.两条直线平行与垂直的判定
对于两条不重合的直线,
或
(1)
(2)l1⊥ l2
或
问题1:在直角坐标系内确定一条直线,需要哪些几何要素?
(1)已知直线上一点 和直线的倾斜角(或斜率 ).
(2)已知直线上两点.
问题2:能否用给定的条件(点 和斜率 或的坐标),将直线上所有点的
坐标满足的关系表示出来 ?
问题引入
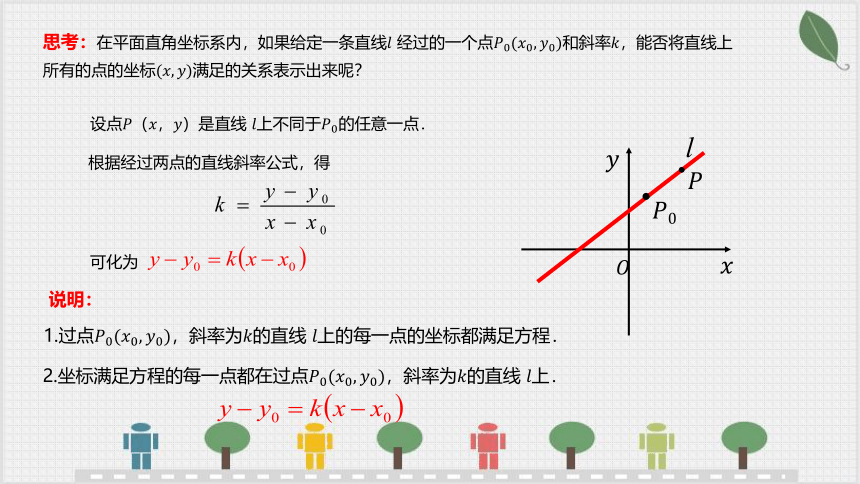
根据经过两点的直线斜率公式,得
设点是直线 上不同于的任意一点.
.
.
可化为
l
思考:在平面直角坐标系内,如果给定一条直线 经过的一个点和斜率,能否将直线上
所有的点的坐标满足的关系表示出来呢?
1.过点,斜率为的直线 上的每一点的坐标都满足方程.
说明:
2.坐标满足方程的每一点都在过点,斜率为的直线 上.
方程由直线上一点及其斜率确定,因此,我们把它叫做直线的点斜式方程,简称点斜式.
新知讲解
直线的点斜式方程:
过点,斜率为的直线
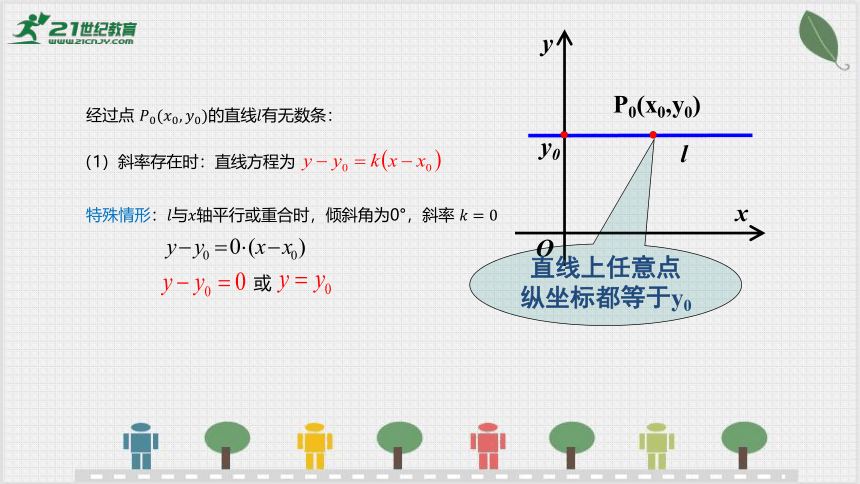
特殊情形:轴平行或重合时,倾斜角为0°,斜率
经过点 的直线有无数条:
或
(1)斜率存在时:直线方程为
l
x
y
O
P0(x0,y0)
y0
直线上任意点
纵坐标都等于y0
x
y
l
直线上任意点
横坐标都等于x0
O
P0(x0,y0)
或
直线与轴垂直,斜率不存在,
不能用点斜式求方程
(2)斜率不存在时:直线的倾斜角为90°,
例1 直线经过点p0(-2,3),且倾斜角α=45°,求直线 的点斜式方程,并画出图形 .
代入点斜式方程得:
y-3=x+2
解:直线经过点p0(-2,3) ,斜率k=tan45°=1,
y
1
2
3
4
x
O
-1
-2
l
典例剖析
如图所示.
例2 已知直线点A(3,-5)和B(-2,5),求直线的方程.
解:∵直线过点A(3,-5)和B(-2,5)
将A(3,-5),代入点斜式方程,得
1.写出下列直线的点斜式方程:
(1)
2.说出下列点斜式方程所对应的直线的斜率和倾斜角:
跟踪训练
(1)斜率为1,倾斜角为
(2)方程可变形为
斜率为,倾斜角为
O
x
y
.
(0,b)
已知直线 过点斜率为,这时直线 与 轴的交点,
代入点斜式方程,得:
即 .
我们把直线与轴交点的纵坐标叫做直线在轴上的截距.
方程由直线的斜率与它在轴上的截距确定,我们把该方程叫做直线的斜截式方程,
简称斜截式.
l
点斜式的特殊情形:
新知讲解
斜截式方程:
y的系数为1
直线的斜率
在y轴上的截距
斜截式方程的特点
直线与y轴的交点是(0,b)
截距是不是距离?
是不是一定要为正?
思考1 :能否用斜截式方程表示直角坐标平面内的所有直线
不能,直线的斜率k必须存在.
思考2:直线的斜截式方程与一次函数有什么关系?
直线方程的斜截式即是一次函数的解析式.
例3 求斜率是5,在轴上的截距是4的直线方程.
解:由已知得k =5, b= 4,
代入斜截式方程,得
y= 5x+4
典例剖析
跟踪训练
1.写出下列直线的斜截式方程:
2.写出下列直线的斜率和在轴上的截距:
解:(1)斜率:在轴上的截距:
(2)斜率:3; 在轴上的截距:0
(3)斜率:0; 在轴上的截距:3
(4)可变形为斜率:在轴上的截距:
∥
1
l
2
1
2
1
-
=
^
k
k
l
∥
,
l
2
1
2
1
2
1
=
b
b
k
k
l
且
判断下列各直线是否平行或垂直
(1)
(2)
跟踪训练
注意:直线的点斜式,斜截式方程在直线斜率存在时才可以应用.
2.斜截式方程:
1.点斜式方程:
4.直线
几何意义:
3.直线与轴垂直时,倾斜角α=90°
或
课堂小结
是直线的斜率,是直线在轴上的截距
谢 谢!
2.2.1 直线的点斜式方程
第二章
2.2
直线的方程
学习目标
1.掌握直线方程的点斜式和斜截式,并会用它们求直线的方程.
2.了解直线的斜截式方程与一次函数的关系.
3. 会用直线的点斜式方程与斜截式方程解决直线的平行与垂直问题.
核心素养:数学抽象、数学运算、逻辑推理
1.直线的斜率公式
注意:不是所有的直线都有斜率,
斜率不存在的直线为与轴垂直的直线.
新知学习
链接回顾
(1)tan
(2)( )
2.两条直线平行与垂直的判定
对于两条不重合的直线,
或
(1)
(2)l1⊥ l2
或
问题1:在直角坐标系内确定一条直线,需要哪些几何要素?
(1)已知直线上一点 和直线的倾斜角(或斜率 ).
(2)已知直线上两点.
问题2:能否用给定的条件(点 和斜率 或的坐标),将直线上所有点的
坐标满足的关系表示出来 ?
问题引入
根据经过两点的直线斜率公式,得
设点是直线 上不同于的任意一点.
.
.
可化为
l
思考:在平面直角坐标系内,如果给定一条直线 经过的一个点和斜率,能否将直线上
所有的点的坐标满足的关系表示出来呢?
1.过点,斜率为的直线 上的每一点的坐标都满足方程.
说明:
2.坐标满足方程的每一点都在过点,斜率为的直线 上.
方程由直线上一点及其斜率确定,因此,我们把它叫做直线的点斜式方程,简称点斜式.
新知讲解
直线的点斜式方程:
过点,斜率为的直线
特殊情形:轴平行或重合时,倾斜角为0°,斜率
经过点 的直线有无数条:
或
(1)斜率存在时:直线方程为
l
x
y
O
P0(x0,y0)
y0
直线上任意点
纵坐标都等于y0
x
y
l
直线上任意点
横坐标都等于x0
O
P0(x0,y0)
或
直线与轴垂直,斜率不存在,
不能用点斜式求方程
(2)斜率不存在时:直线的倾斜角为90°,
例1 直线经过点p0(-2,3),且倾斜角α=45°,求直线 的点斜式方程,并画出图形 .
代入点斜式方程得:
y-3=x+2
解:直线经过点p0(-2,3) ,斜率k=tan45°=1,
y
1
2
3
4
x
O
-1
-2
l
典例剖析
如图所示.
例2 已知直线点A(3,-5)和B(-2,5),求直线的方程.
解:∵直线过点A(3,-5)和B(-2,5)
将A(3,-5),代入点斜式方程,得
1.写出下列直线的点斜式方程:
(1)
2.说出下列点斜式方程所对应的直线的斜率和倾斜角:
跟踪训练
(1)斜率为1,倾斜角为
(2)方程可变形为
斜率为,倾斜角为
O
x
y
.
(0,b)
已知直线 过点斜率为,这时直线 与 轴的交点,
代入点斜式方程,得:
即 .
我们把直线与轴交点的纵坐标叫做直线在轴上的截距.
方程由直线的斜率与它在轴上的截距确定,我们把该方程叫做直线的斜截式方程,
简称斜截式.
l
点斜式的特殊情形:
新知讲解
斜截式方程:
y的系数为1
直线的斜率
在y轴上的截距
斜截式方程的特点
直线与y轴的交点是(0,b)
截距是不是距离?
是不是一定要为正?
思考1 :能否用斜截式方程表示直角坐标平面内的所有直线
不能,直线的斜率k必须存在.
思考2:直线的斜截式方程与一次函数有什么关系?
直线方程的斜截式即是一次函数的解析式.
例3 求斜率是5,在轴上的截距是4的直线方程.
解:由已知得k =5, b= 4,
代入斜截式方程,得
y= 5x+4
典例剖析
跟踪训练
1.写出下列直线的斜截式方程:
2.写出下列直线的斜率和在轴上的截距:
解:(1)斜率:在轴上的截距:
(2)斜率:3; 在轴上的截距:0
(3)斜率:0; 在轴上的截距:3
(4)可变形为斜率:在轴上的截距:
∥
1
l
2
1
2
1
-
=
^
k
k
l
∥
,
l
2
1
2
1
2
1
=
b
b
k
k
l
且
判断下列各直线是否平行或垂直
(1)
(2)
跟踪训练
注意:直线的点斜式,斜截式方程在直线斜率存在时才可以应用.
2.斜截式方程:
1.点斜式方程:
4.直线
几何意义:
3.直线与轴垂直时,倾斜角α=90°
或
课堂小结
是直线的斜率,是直线在轴上的截距
谢 谢!
