2.1.2两条直线平行和垂直的判定 课件(共20页)
文档属性
| 名称 | 2.1.2两条直线平行和垂直的判定 课件(共20页) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:26:06 | ||
图片预览





文档简介
(共20张PPT)
2.1.2 两条直线平行和垂直的判定
第二章
2.1
直线的倾斜角与斜率
学习目标
1.理解两条直线平行与垂直的条件.
2.能根据直线的斜率判定两条直线平行或垂直.
3.能利用两直线平行或垂直的条件解决问题.
核心素养:数学抽象、数学运算、逻辑推理
1.直线的倾斜角的定义
2.直线的斜率的定义
3.过两点P1 ( x1 ,y1), P2 ( x2 ,y2)的直线的斜率公式
· 当直线与轴相交时,我们取轴作为基准,轴正向与直线 向上方向之间所成的
角α 叫做直线 的倾斜角.
· 当直线与x轴重合或平行时,规定它的倾斜角为0°.
倾斜角α不是90°的直线,它的倾斜角α的正切值叫做这条直线的斜率,=tanα (α≠90°)
新知学习
链接回顾
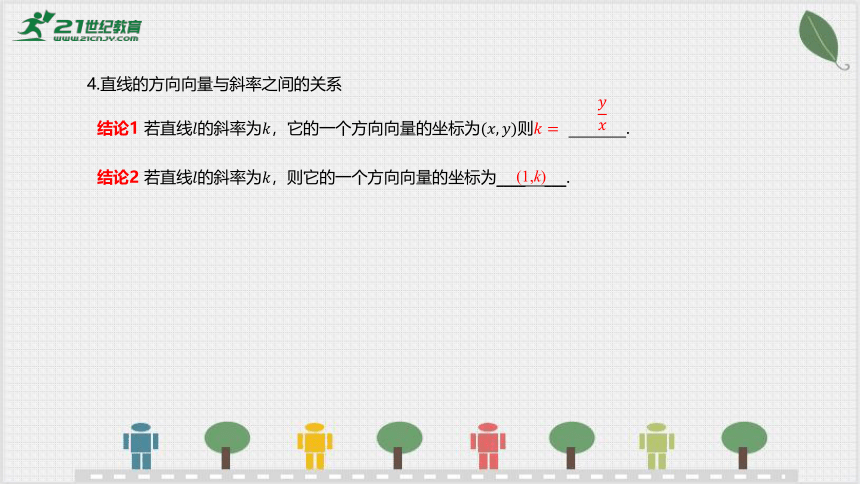
4.直线的方向向量与斜率之间的关系
结论2 若直线的斜率为,则它的一个方向向量的坐标为____ ___.
(1,k)
结论1 若直线的斜率为,它的一个方向向量的坐标为则 .
过山车是一项富有刺激性的娱乐项目.实际上,过山车的运动包含了许多数学和物理学原理.过山车的两条铁轨是相互平行的轨道,它们靠着一根根巨大的柱形钢筋支撑着,为了使设备安全,柱子之间还有一些小的钢筋连接,这些钢筋有的互相平行,有的互相垂直,你能感受到过山车中的平行和垂直吗 两条直线的平行与垂直用什么来刻画呢
情景引入
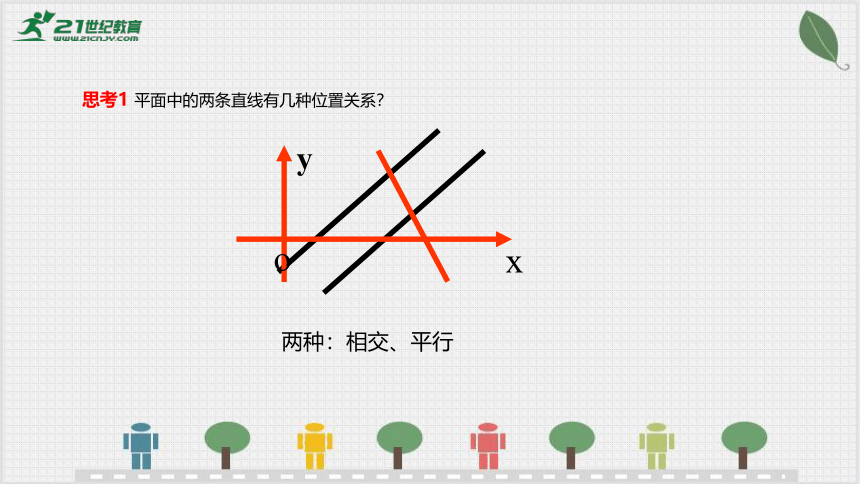
思考1 平面中的两条直线有几种位置关系?
o
x
y
两种:相交、平行
o
x
y
l1
l2
l1
l2
l1
l2
l1
l2
l1
l2
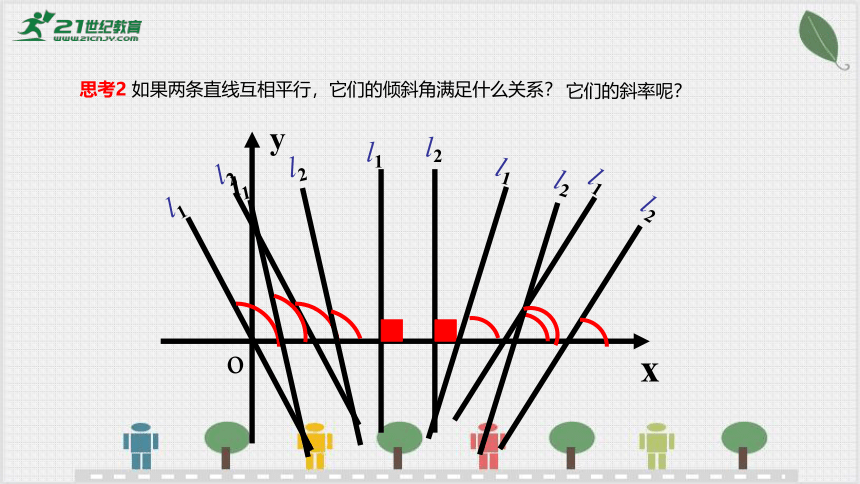
思考2 如果两条直线互相平行,它们的倾斜角满足什么关系?
它们的斜率呢?
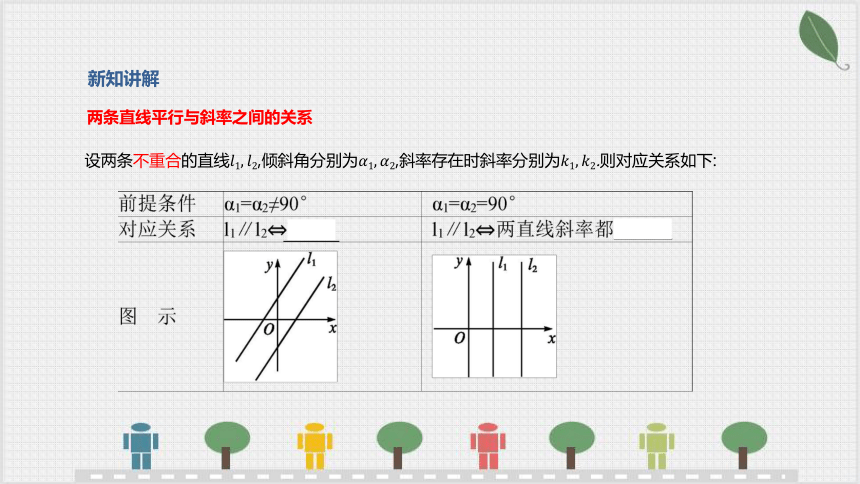
两条直线平行与斜率之间的关系
设两条不重合的直线,倾斜角分别为,斜率存在时斜率分别为.则对应关系如下:
新知讲解
1.对于两条不重合的直线“”是“两条直线斜率相等”的什么条件
2.已知直线经过两点直线经过两点且 ,
则 .
解析:由题意知l1⊥x轴.又l1∥l2,所以l2⊥x轴,故x=2.
解:如果两不重合直线斜率相等,则两直线一定平行;反过来,两直线平行,有可能两直线斜率均不存在.
故“”是“两条直线斜率相等”的必要不充分条件.
2
即时巩固
例1 已知试判断直线
的位置关系,并证明你的结论.
O
A
B
P
Q
∴结合
典例剖析
例2 已知四边形的四个顶点分别为,试判断四边形的形状,并给出证明.
O
x
y
D
C
A
B
∥
∥
已知三点,这三点是否在同一条直线上,为什么?
解:
又 ∵直线与有公共点,
∴三点在一条直线上.
跟踪训练
y
l2
O
x
l1
α2
当两条直线相交时,它们的斜率不相等;反之,当两条直线的斜率不相等时,它们相交.
在相交直线中,垂直是最特殊的情形.
α1
α1
思考3 当直线时,它们的斜率除了不相等外,是否还存在特殊的数量关系?
设两条直线的斜率分别为.则:
(1,k1)
直线的一个方向向量= .
(1,k2)
直线的一个方向向量= ;
l1⊥ l2
=0
1×1+k1k2=0
k1k2=
新知探究
两条直线垂直与斜率之间的关系
注意:“两条直线的斜率之积等于-1”是“这两条直线垂直”的充分不必要条件.因为两条直线
垂直时,除了斜率之积等于-1,还有可能一条直线的斜率不存在,另一条直线的斜率为0.
新知讲解
3.若直线的斜率是方程的两根,则与的位置关系是 .
解析:由一元二次方程根与系数的关系,知k1k2=-1,
所以l1⊥l2.
4.已知直线, ⊥ ,且的斜率是,则直线的斜率是___________________.
解析:当a=0时,直线l1垂直于y轴,由于l1⊥l2 ,所以l2⊥x轴,即直线l2的斜率不存在;
当a≠0时,由于l1⊥l2 ,所以k1k2=-1 ,所以k2=-.
不存在
l1⊥l2
即时巩固
例3 已知判断直线与的位置关系.
解:直线AB的斜率
直线PQ的斜率
例4 已知三点,试判断的形状.
C ·
·A
B ·
跟踪训练
试确定的值,使过点的直线与过点的直线
(1)平行; (2)垂直.
解:过点的直线的斜率
(1)若过点的直线与过点的直线平行,则
即
解得
所以当 时,过点的直线与过点的直线平行.
(2)若过点的直线与过点的直线垂直,则
即
解得
所以当 时,过点的直线与过点的直线垂直.
结论1:对于两条不重合的直线,
l1∥l2 k1=k2.
条件:不重合、都有斜率
l1⊥l2 k1k2=-1.
条件:都有斜率
l1⊥ l2
或
或
结论2:对于任意两条直线,
课堂小结
谢 谢!
2.1.2 两条直线平行和垂直的判定
第二章
2.1
直线的倾斜角与斜率
学习目标
1.理解两条直线平行与垂直的条件.
2.能根据直线的斜率判定两条直线平行或垂直.
3.能利用两直线平行或垂直的条件解决问题.
核心素养:数学抽象、数学运算、逻辑推理
1.直线的倾斜角的定义
2.直线的斜率的定义
3.过两点P1 ( x1 ,y1), P2 ( x2 ,y2)的直线的斜率公式
· 当直线与轴相交时,我们取轴作为基准,轴正向与直线 向上方向之间所成的
角α 叫做直线 的倾斜角.
· 当直线与x轴重合或平行时,规定它的倾斜角为0°.
倾斜角α不是90°的直线,它的倾斜角α的正切值叫做这条直线的斜率,=tanα (α≠90°)
新知学习
链接回顾
4.直线的方向向量与斜率之间的关系
结论2 若直线的斜率为,则它的一个方向向量的坐标为____ ___.
(1,k)
结论1 若直线的斜率为,它的一个方向向量的坐标为则 .
过山车是一项富有刺激性的娱乐项目.实际上,过山车的运动包含了许多数学和物理学原理.过山车的两条铁轨是相互平行的轨道,它们靠着一根根巨大的柱形钢筋支撑着,为了使设备安全,柱子之间还有一些小的钢筋连接,这些钢筋有的互相平行,有的互相垂直,你能感受到过山车中的平行和垂直吗 两条直线的平行与垂直用什么来刻画呢
情景引入
思考1 平面中的两条直线有几种位置关系?
o
x
y
两种:相交、平行
o
x
y
l1
l2
l1
l2
l1
l2
l1
l2
l1
l2
思考2 如果两条直线互相平行,它们的倾斜角满足什么关系?
它们的斜率呢?
两条直线平行与斜率之间的关系
设两条不重合的直线,倾斜角分别为,斜率存在时斜率分别为.则对应关系如下:
新知讲解
1.对于两条不重合的直线“”是“两条直线斜率相等”的什么条件
2.已知直线经过两点直线经过两点且 ,
则 .
解析:由题意知l1⊥x轴.又l1∥l2,所以l2⊥x轴,故x=2.
解:如果两不重合直线斜率相等,则两直线一定平行;反过来,两直线平行,有可能两直线斜率均不存在.
故“”是“两条直线斜率相等”的必要不充分条件.
2
即时巩固
例1 已知试判断直线
的位置关系,并证明你的结论.
O
A
B
P
Q
∴结合
典例剖析
例2 已知四边形的四个顶点分别为,试判断四边形的形状,并给出证明.
O
x
y
D
C
A
B
∥
∥
已知三点,这三点是否在同一条直线上,为什么?
解:
又 ∵直线与有公共点,
∴三点在一条直线上.
跟踪训练
y
l2
O
x
l1
α2
当两条直线相交时,它们的斜率不相等;反之,当两条直线的斜率不相等时,它们相交.
在相交直线中,垂直是最特殊的情形.
α1
α1
思考3 当直线时,它们的斜率除了不相等外,是否还存在特殊的数量关系?
设两条直线的斜率分别为.则:
(1,k1)
直线的一个方向向量= .
(1,k2)
直线的一个方向向量= ;
l1⊥ l2
=0
1×1+k1k2=0
k1k2=
新知探究
两条直线垂直与斜率之间的关系
注意:“两条直线的斜率之积等于-1”是“这两条直线垂直”的充分不必要条件.因为两条直线
垂直时,除了斜率之积等于-1,还有可能一条直线的斜率不存在,另一条直线的斜率为0.
新知讲解
3.若直线的斜率是方程的两根,则与的位置关系是 .
解析:由一元二次方程根与系数的关系,知k1k2=-1,
所以l1⊥l2.
4.已知直线, ⊥ ,且的斜率是,则直线的斜率是___________________.
解析:当a=0时,直线l1垂直于y轴,由于l1⊥l2 ,所以l2⊥x轴,即直线l2的斜率不存在;
当a≠0时,由于l1⊥l2 ,所以k1k2=-1 ,所以k2=-.
不存在
l1⊥l2
即时巩固
例3 已知判断直线与的位置关系.
解:直线AB的斜率
直线PQ的斜率
例4 已知三点,试判断的形状.
C ·
·A
B ·
跟踪训练
试确定的值,使过点的直线与过点的直线
(1)平行; (2)垂直.
解:过点的直线的斜率
(1)若过点的直线与过点的直线平行,则
即
解得
所以当 时,过点的直线与过点的直线平行.
(2)若过点的直线与过点的直线垂直,则
即
解得
所以当 时,过点的直线与过点的直线垂直.
结论1:对于两条不重合的直线,
l1∥l2 k1=k2.
条件:不重合、都有斜率
l1⊥l2 k1k2=-1.
条件:都有斜率
l1⊥ l2
或
或
结论2:对于任意两条直线,
课堂小结
谢 谢!
