2.3.1两条直线的交点坐标 课件(共23页)
文档属性
| 名称 | 2.3.1两条直线的交点坐标 课件(共23页) |  | |
| 格式 | pptx | ||
| 文件大小 | 960.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:26:06 | ||
图片预览






文档简介
(共23张PPT)
2.3.1 两条直线的交点坐标
第二章
2.3
直线的交点坐标与距离公式
学习目标
1.能用解方程组的方法判断两直线的位置关系.
2.能用解方程组的方法求两相交直线的交点坐标.
核心素养:数学运算、逻辑推理
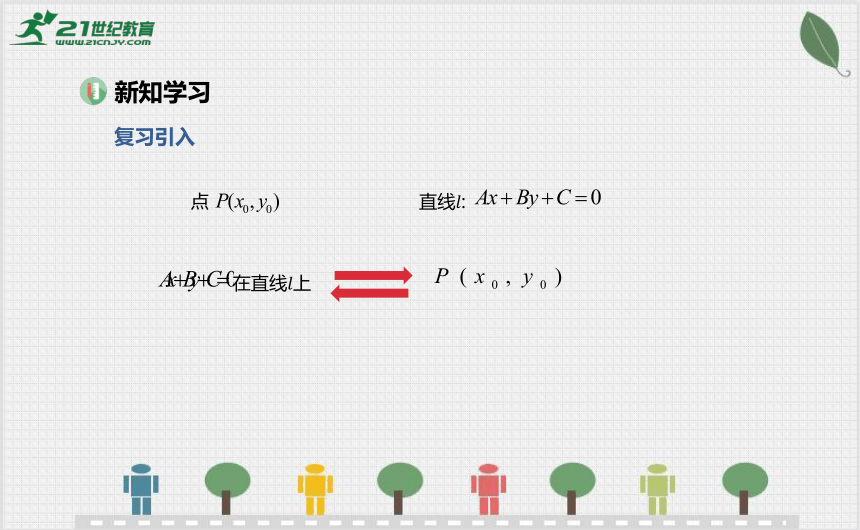
点
直线:
在直线上
新知学习
复习引入
思考1:已知两条直线 , 相交,它们的交点坐标与直线的方程有什么关系?你能由此得到求两条相交直线交点坐标的方法吗?
设这两条直线的交点为,则点既在直线上,也在直线上.
所以点的坐标既满足直线的方程,也满足直线的方程,
即点的坐标是方程组 的解.
解这个方程组就可以得到这两条直线的交点坐标.
新知讲解
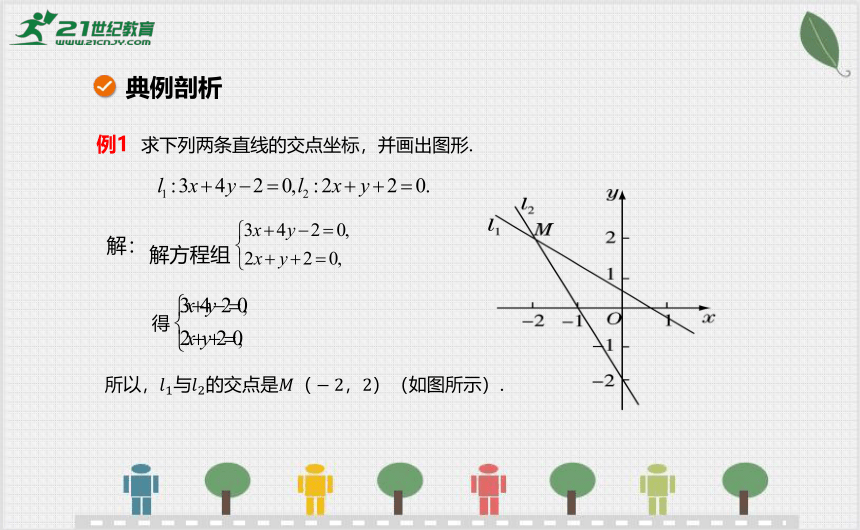
例1 求下列两条直线的交点坐标,并画出图形.
解:
典例剖析
得
所以,与的交点是(如图所示).
直线和相交.
两条直线
相交
方程组有
唯一解
的唯一解.
直线和存在唯一交点,记为
点 既在上,又在
两条直线没有公共点
不存在点同时满足两条直线方程
方程组无解
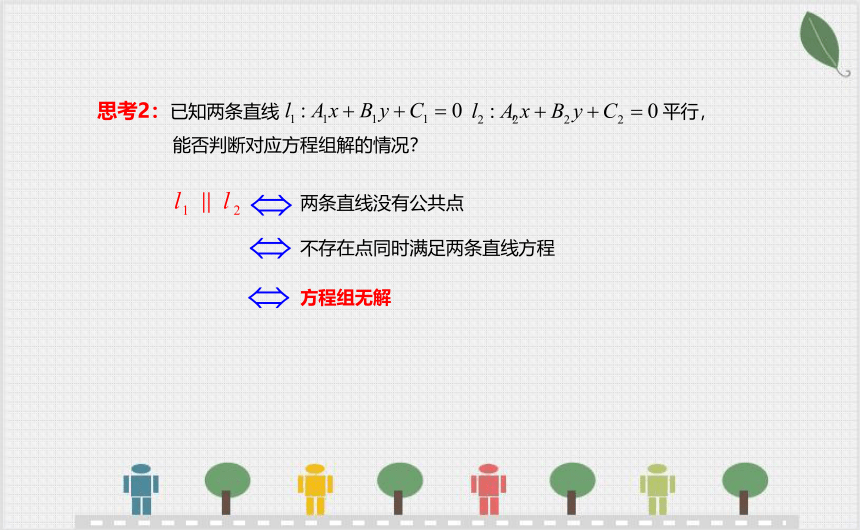
思考2:已知两条直线 , 平行,
能否判断对应方程组解的情况?
两条直线没有公共点
不存在点同时满足两条直线方程
方程组无解
思考2:已知两条直线 , 平行,
能否判断对应方程组解的情况?
两条直线没有公共点
不存在点同时满足两条直线方程
方程组无解
思考2:已知两条直线 , 平行,
能否判断对应方程组解的情况?
两条直线有无数个公共点
存在无数个点同时满足两条直线方程
方程组有无数组解
直线和重合
方程组
已知两条直线 , ,
解的组数与两条直线的位置关系如下表:
方程组的解 一组 无数组 无解
直线与的公共点的个数 无数个
直线的位置关系
一个
相交
重合
零个
平行
例2 判断下列各对直线的位置关系.如果相交,求出交点的坐标.
所以,直线与相交,交点坐标为 .
得
,
矛盾,这个方程组无解,
所以直线与无公共点,
解:(1) 将两条直线方程化为斜截式:
斜率不相等, 与 相交.
例2 判断下列各对直线的位置关系.如果相交,求出交点的坐标.
思考:能否用直线的
斜率判断两对直线的
位置关系?
(2)
斜率相等,截距不相等,则 平行.
斜率判断 解方程组判断
与 重合,有无数个交点.
两个方程相同,
方程组有无数个解.
能否用直线的斜率和解方程组,这两种方法判断两条直线
的位置关系,并确定
交点个数呢?
跟踪训练
思考:比较用斜率判断和解方程组判断两直线位置关系这两种方法,你有什么体会?
代数方法
关注直线方程系数关系,快速判断两条直线平行或相交(垂直).
关注解的个数与交点个数的对应,判断两条直线平行或相交;求相交直线交点坐标.
斜率判断
解方程组判断
例3 求满足下列条件的直线的方程:
经过两条直线和的交点,且平行于直线.
经过两条直线和的交点,且垂直于直线.
求交点
求斜率
点斜式
由直线 与直线平行知,的斜率为
整理得
解得交点坐标为 .
所以直线的方程为
.
例3 求满足下列条件的直线的方程:
经过两条直线和的交点,且平行于直线.
经过两条直线和的交点,且垂直于直线.
求交点
求斜率
点斜式
由直线 与直线知,的斜率为
整理得
解得交点坐标为.
所以直线的方程为
.
例3 求满足下列条件的直线的方程:
经过两条直线和的交点,且平行于直线.
经过两条直线和的交点,且垂直于直线.
求交点
设直线系方程
求参数
平行直线系
垂直直线系
求经过两条直线和的交点,
且垂直于直线的直线方程.
跟踪训练
3
随堂小测
1.若三条直线,,相交于一点,则( )
A. B. C.2 D.
B
2.已知直线与直线互相垂直,垂足为,
则的值为( )
A.20 B.C.0 D.24
B
3.设直线与的交点为,则过点且与直线平行的直线的方程为 ;过点且在两坐标轴上的截距互为相反数的直线的方程为 .
求相交直线交点坐标
解方程组
判断两条直线的位置关系
(相交、平行、重合)
解的个数与交点个数的对应
课堂小结
方程组
已知两条直线 , ,
解的组数与两条直线的位置关系如下表:
方程组的解 一组 无数组 无解
直线与的公共点的个数 无数个
直线的位置关系
一个
相交
重合
零个
平行
谢 谢!
2.3.1 两条直线的交点坐标
第二章
2.3
直线的交点坐标与距离公式
学习目标
1.能用解方程组的方法判断两直线的位置关系.
2.能用解方程组的方法求两相交直线的交点坐标.
核心素养:数学运算、逻辑推理
点
直线:
在直线上
新知学习
复习引入
思考1:已知两条直线 , 相交,它们的交点坐标与直线的方程有什么关系?你能由此得到求两条相交直线交点坐标的方法吗?
设这两条直线的交点为,则点既在直线上,也在直线上.
所以点的坐标既满足直线的方程,也满足直线的方程,
即点的坐标是方程组 的解.
解这个方程组就可以得到这两条直线的交点坐标.
新知讲解
例1 求下列两条直线的交点坐标,并画出图形.
解:
典例剖析
得
所以,与的交点是(如图所示).
直线和相交.
两条直线
相交
方程组有
唯一解
的唯一解.
直线和存在唯一交点,记为
点 既在上,又在
两条直线没有公共点
不存在点同时满足两条直线方程
方程组无解
思考2:已知两条直线 , 平行,
能否判断对应方程组解的情况?
两条直线没有公共点
不存在点同时满足两条直线方程
方程组无解
思考2:已知两条直线 , 平行,
能否判断对应方程组解的情况?
两条直线没有公共点
不存在点同时满足两条直线方程
方程组无解
思考2:已知两条直线 , 平行,
能否判断对应方程组解的情况?
两条直线有无数个公共点
存在无数个点同时满足两条直线方程
方程组有无数组解
直线和重合
方程组
已知两条直线 , ,
解的组数与两条直线的位置关系如下表:
方程组的解 一组 无数组 无解
直线与的公共点的个数 无数个
直线的位置关系
一个
相交
重合
零个
平行
例2 判断下列各对直线的位置关系.如果相交,求出交点的坐标.
所以,直线与相交,交点坐标为 .
得
,
矛盾,这个方程组无解,
所以直线与无公共点,
解:(1) 将两条直线方程化为斜截式:
斜率不相等, 与 相交.
例2 判断下列各对直线的位置关系.如果相交,求出交点的坐标.
思考:能否用直线的
斜率判断两对直线的
位置关系?
(2)
斜率相等,截距不相等,则 平行.
斜率判断 解方程组判断
与 重合,有无数个交点.
两个方程相同,
方程组有无数个解.
能否用直线的斜率和解方程组,这两种方法判断两条直线
的位置关系,并确定
交点个数呢?
跟踪训练
思考:比较用斜率判断和解方程组判断两直线位置关系这两种方法,你有什么体会?
代数方法
关注直线方程系数关系,快速判断两条直线平行或相交(垂直).
关注解的个数与交点个数的对应,判断两条直线平行或相交;求相交直线交点坐标.
斜率判断
解方程组判断
例3 求满足下列条件的直线的方程:
经过两条直线和的交点,且平行于直线.
经过两条直线和的交点,且垂直于直线.
求交点
求斜率
点斜式
由直线 与直线平行知,的斜率为
整理得
解得交点坐标为 .
所以直线的方程为
.
例3 求满足下列条件的直线的方程:
经过两条直线和的交点,且平行于直线.
经过两条直线和的交点,且垂直于直线.
求交点
求斜率
点斜式
由直线 与直线知,的斜率为
整理得
解得交点坐标为.
所以直线的方程为
.
例3 求满足下列条件的直线的方程:
经过两条直线和的交点,且平行于直线.
经过两条直线和的交点,且垂直于直线.
求交点
设直线系方程
求参数
平行直线系
垂直直线系
求经过两条直线和的交点,
且垂直于直线的直线方程.
跟踪训练
3
随堂小测
1.若三条直线,,相交于一点,则( )
A. B. C.2 D.
B
2.已知直线与直线互相垂直,垂足为,
则的值为( )
A.20 B.C.0 D.24
B
3.设直线与的交点为,则过点且与直线平行的直线的方程为 ;过点且在两坐标轴上的截距互为相反数的直线的方程为 .
求相交直线交点坐标
解方程组
判断两条直线的位置关系
(相交、平行、重合)
解的个数与交点个数的对应
课堂小结
方程组
已知两条直线 , ,
解的组数与两条直线的位置关系如下表:
方程组的解 一组 无数组 无解
直线与的公共点的个数 无数个
直线的位置关系
一个
相交
重合
零个
平行
谢 谢!
