2.3.2两点间的距离公式 课件(共14页)
文档属性
| 名称 | 2.3.2两点间的距离公式 课件(共14页) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:26:06 | ||
图片预览






文档简介
(共14张PPT)
2.3.2 两点间的距离公式
第二章
2.3
直线的交点坐标与距离公式
学习目标
1.探索并掌握两点间的距离公式.
2.会用坐标法解决平面几何中的问题.
核心素养:数学抽象、数学运算、逻辑推理
探究: 已知平面内两点,如何求间的距离呢
如图所示,
于是,.
由此得到两点间的距离公式
由点,得.
特别地,
①原点与任一点间的距离.
③当直线垂直于轴时,| |=||.
两点间的距离公式与两点的先后顺序无关
②当直线垂直于轴时,| |=||.
新知学习
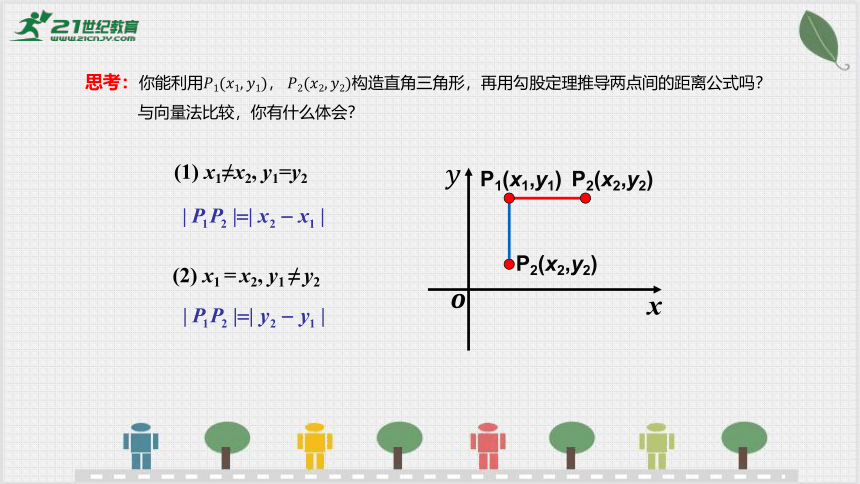
(1) x1≠x2, y1=y2
(2) x1 = x2, y1 ≠ y2
P1(x1,y1)
P2(x2,y2)
P2(x2,y2)
x
思考:你能利用构造直角三角形,再用勾股定理推导两点间的距离公式吗?
与向量法比较,你有什么体会?
(3) x1 ≠ x2, y1 ≠ y2
Q
(x2,y1)
y
x
P1
P2
(x1,y1)
(x2,y2)
思考:你能利用构造直角三角形,再用勾股定理推导两点间的距离公式吗?
与向量法比较,你有什么体会?
求下列两点间的距离:
(1) ;
(2) ;
(3) ;
(4)
即时巩固
∴所求点为,
典例剖析
解:设点的坐标为,
例1 已知点在轴上求一点,使,并求的值.
,
.
由,得
.
解得.
且
例2 证明:平行四边形四条边的平方和等于两条对角线的平方和.
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
解:如图,以顶点为坐标原点,边所在的直线为轴,建立平面直角坐标系,
则有A(0,0).
设
由平行四边形的性质,得
.
例2 证明:平行四边形四条边的平方和等于两条对角线的平方和.
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
由两点间的距离公式,得
,
,
,
即平行四边形四条边的平方和等于两条对角线的平方和.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算的结果“翻译”成几何结论.
反思感悟 利用“坐标法”解决平面几何问题的基本步骤
1.已知点和间的距离为5,则 .
随堂小测
或
2.已知点.求证:为直角三角形.
3.在中,是边上任意一点(不重合),且
求证:为等腰三角形.
设.
证明两边相等.
1.两点间的距离公式
2
2
|
|
y
x
OP
+
=
(2)原点与任一点间的距离
课堂小结
(1)平面内两点间的距离
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算的结果“翻译”成几何结论.
2.利用“坐标法”解决平面几何问题的基本步骤
谢 谢!
2.3.2 两点间的距离公式
第二章
2.3
直线的交点坐标与距离公式
学习目标
1.探索并掌握两点间的距离公式.
2.会用坐标法解决平面几何中的问题.
核心素养:数学抽象、数学运算、逻辑推理
探究: 已知平面内两点,如何求间的距离呢
如图所示,
于是,.
由此得到两点间的距离公式
由点,得.
特别地,
①原点与任一点间的距离.
③当直线垂直于轴时,| |=||.
两点间的距离公式与两点的先后顺序无关
②当直线垂直于轴时,| |=||.
新知学习
(1) x1≠x2, y1=y2
(2) x1 = x2, y1 ≠ y2
P1(x1,y1)
P2(x2,y2)
P2(x2,y2)
x
思考:你能利用构造直角三角形,再用勾股定理推导两点间的距离公式吗?
与向量法比较,你有什么体会?
(3) x1 ≠ x2, y1 ≠ y2
Q
(x2,y1)
y
x
P1
P2
(x1,y1)
(x2,y2)
思考:你能利用构造直角三角形,再用勾股定理推导两点间的距离公式吗?
与向量法比较,你有什么体会?
求下列两点间的距离:
(1) ;
(2) ;
(3) ;
(4)
即时巩固
∴所求点为,
典例剖析
解:设点的坐标为,
例1 已知点在轴上求一点,使,并求的值.
,
.
由,得
.
解得.
且
例2 证明:平行四边形四条边的平方和等于两条对角线的平方和.
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
解:如图,以顶点为坐标原点,边所在的直线为轴,建立平面直角坐标系,
则有A(0,0).
设
由平行四边形的性质,得
.
例2 证明:平行四边形四条边的平方和等于两条对角线的平方和.
y
x
o
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
由两点间的距离公式,得
,
,
,
即平行四边形四条边的平方和等于两条对角线的平方和.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算的结果“翻译”成几何结论.
反思感悟 利用“坐标法”解决平面几何问题的基本步骤
1.已知点和间的距离为5,则 .
随堂小测
或
2.已知点.求证:为直角三角形.
3.在中,是边上任意一点(不重合),且
求证:为等腰三角形.
设.
证明两边相等.
1.两点间的距离公式
2
2
|
|
y
x
OP
+
=
(2)原点与任一点间的距离
课堂小结
(1)平面内两点间的距离
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算的结果“翻译”成几何结论.
2.利用“坐标法”解决平面几何问题的基本步骤
谢 谢!
