2.4.1圆标准方程 课件(共19页)
文档属性
| 名称 | 2.4.1圆标准方程 课件(共19页) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 08:47:00 | ||
图片预览






文档简介
(共19张PPT)
2.4
圆的方程
第二章
2.4.1 圆的标准方程
1.会用定义推导圆的标准方程,并掌握圆的标准方程的特征.
2.能根据所给条件求圆的标准方程.
3.掌握点与圆的位置关系并能解决相关问题.
核心素养:数学抽象、数学运算
学习目标
月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写.如果把天空看作一个平面,月亮当做一个圆,建立一个平面直角坐标系,那么圆的坐标满足的方程如何表示
《古朗月行》
唐 李白
小时不识月,
呼作白玉盘。
又疑瑶台镜,
飞在青云端。
A
r
x
y
O
情境导学
新知学习
问题1 什么是圆?初中时我们是怎样给圆下定义的?
平面内与定点距离等于定长的点的集合(轨迹)是圆.
问题2 平面直角坐标系中,如何确定一个圆?
圆心:确定圆的位置
半径:确定圆的大小
定点
定长
确定圆的几何要素:圆心和半径
A
r
探究新知
问题3 圆心是A(a,b),半径是r的圆的方程是什么?
x
y
O
A(a,b)
M(x,y)
P = { M | |MA| = r }
圆上所有点的集合
设点M (x,y)为圆A上任一点,则|MA|= r.
r
思考 是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上?
点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.
x
y
O
A(a,b)
M(x,y)
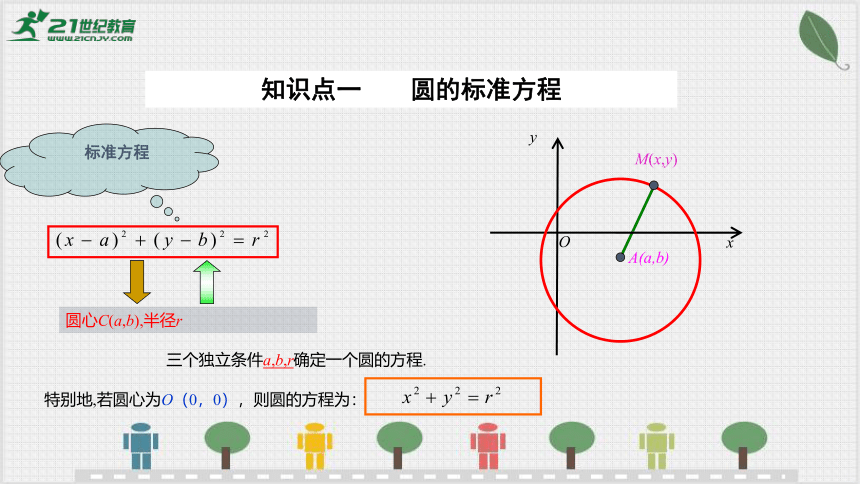
圆心C(a,b),半径r
特别地,若圆心为O(0,0),则圆的方程为:
标准方程
知识点一 圆的标准方程
三个独立条件a,b,r确定一个圆的方程.
1 .(口答) 说出下列圆的圆心及半径
(5)x2 + y2 4x + 10y + 28 = 0
圆心C(2, 5), r = 1
圆心C(a, 0),
(6)(x a)2 + y 2 = m2
(7) x 2 + (y+3a) 2 = -4m (m<0)
圆心C( 0,-3a),
2 .写出下列圆的方程
(1) 圆心在(-3,4),半径为;
(2) 圆心在原点,半径为3;
(3) 圆心在点C(3, -4), 半径为7.
(1
(2) x 2 + y 2 =9
(3) (x 3)2 +( y+4) 2 = 49
即时巩固
例1 写出圆心为,半径长等于5的圆的方程,并判断点是否在这个圆上.
解:圆心是,半径长等于5的圆的标准方程是:
把点的坐标代入方程 左右两边相等,点的坐标适合圆的方程,所以点 在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点的坐标不适合圆的方程,所以点不在这个圆上.
典例剖析
探究 在平面几何中,如何确定点与圆的位置关系?
M
A
|AM||AM|=r
A
M
A
M
|AM|>r
点在圆内
点在圆上
点在圆外
探究新知
点M在圆A内;
点M在圆A上;
点M在圆A外.
M
A
A
M
A
M
知识点二 点与圆的位置关系
1.点P(-2,-2)和圆x2+y2=4的位置关系是( )
A.在圆上 B.在圆外 C.在圆内 D.以上都不对
[0,1)
解析:将点P的坐标代入圆的方程,则(-2)2+(-2)2=8>4,故点P在圆外.
B
跟踪训练
2.已知点M(5+1,)在圆(x-1)2+y2=26的内部,则a的取值范围是 .
解析:由题意知解得0≤a<1.
待定系数法
解:设所求圆的方程为:
因为都在圆上
所求圆的方程为
例2 的三个顶点的坐标分别是求它的外接圆的方程.
典例剖析
解法1:设圆心C的坐标为.
因为圆心C在直线上,所以.①
因为是圆上两点,所以|.
根据两点间距离公式,有,即.②
由①②可得.
所以圆心C的坐标是.圆的半径.
所以,所求圆的标准方程是.
例3 已知圆心为C的圆经过两点,且圆心C在直线上,求此圆的
标准方程.
典例剖析
【分析】设圆心C的坐标为.由已知条件可知,|,且.由此可求出圆心坐标和半径.
另外,因为线段是圆的一条弦,根据平面几何知识,的中点与圆心的连线垂直于,由此可得到另一种解法.
待定系数法
解法2:如图,设线段AB的中点为.
由两点的坐标为
可得点的坐标为直线的斜率为.
因此,线段的垂直平分线l′的方程是,即.
由垂径定理可知,圆心也在线段的垂直平分线上,
所以它的坐标是方程组的解.解这个方程组,得
所以圆心C的坐标是.圆的半径.
所以,所求圆的标准方程是.
例3 已知圆心为C的圆经过两点,且圆心C在直线上,求此圆的
标准方程.
典例剖析
几何性质法
归纳总结 圆的标准方程的两种求法
(1)几何法
它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
跟踪训练 已知的顶点坐标分别是 求外接圆的方程.
求出圆的圆心和半径
课堂小结
谢 谢!
2.4
圆的方程
第二章
2.4.1 圆的标准方程
1.会用定义推导圆的标准方程,并掌握圆的标准方程的特征.
2.能根据所给条件求圆的标准方程.
3.掌握点与圆的位置关系并能解决相关问题.
核心素养:数学抽象、数学运算
学习目标
月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写.如果把天空看作一个平面,月亮当做一个圆,建立一个平面直角坐标系,那么圆的坐标满足的方程如何表示
《古朗月行》
唐 李白
小时不识月,
呼作白玉盘。
又疑瑶台镜,
飞在青云端。
A
r
x
y
O
情境导学
新知学习
问题1 什么是圆?初中时我们是怎样给圆下定义的?
平面内与定点距离等于定长的点的集合(轨迹)是圆.
问题2 平面直角坐标系中,如何确定一个圆?
圆心:确定圆的位置
半径:确定圆的大小
定点
定长
确定圆的几何要素:圆心和半径
A
r
探究新知
问题3 圆心是A(a,b),半径是r的圆的方程是什么?
x
y
O
A(a,b)
M(x,y)
P = { M | |MA| = r }
圆上所有点的集合
设点M (x,y)为圆A上任一点,则|MA|= r.
r
思考 是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上?
点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.
x
y
O
A(a,b)
M(x,y)
圆心C(a,b),半径r
特别地,若圆心为O(0,0),则圆的方程为:
标准方程
知识点一 圆的标准方程
三个独立条件a,b,r确定一个圆的方程.
1 .(口答) 说出下列圆的圆心及半径
(5)x2 + y2 4x + 10y + 28 = 0
圆心C(2, 5), r = 1
圆心C(a, 0),
(6)(x a)2 + y 2 = m2
(7) x 2 + (y+3a) 2 = -4m (m<0)
圆心C( 0,-3a),
2 .写出下列圆的方程
(1) 圆心在(-3,4),半径为;
(2) 圆心在原点,半径为3;
(3) 圆心在点C(3, -4), 半径为7.
(1
(2) x 2 + y 2 =9
(3) (x 3)2 +( y+4) 2 = 49
即时巩固
例1 写出圆心为,半径长等于5的圆的方程,并判断点是否在这个圆上.
解:圆心是,半径长等于5的圆的标准方程是:
把点的坐标代入方程 左右两边相等,点的坐标适合圆的方程,所以点 在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点的坐标不适合圆的方程,所以点不在这个圆上.
典例剖析
探究 在平面几何中,如何确定点与圆的位置关系?
M
A
|AM|
A
M
A
M
|AM|>r
点在圆内
点在圆上
点在圆外
探究新知
点M在圆A内;
点M在圆A上;
点M在圆A外.
M
A
A
M
A
M
知识点二 点与圆的位置关系
1.点P(-2,-2)和圆x2+y2=4的位置关系是( )
A.在圆上 B.在圆外 C.在圆内 D.以上都不对
[0,1)
解析:将点P的坐标代入圆的方程,则(-2)2+(-2)2=8>4,故点P在圆外.
B
跟踪训练
2.已知点M(5+1,)在圆(x-1)2+y2=26的内部,则a的取值范围是 .
解析:由题意知解得0≤a<1.
待定系数法
解:设所求圆的方程为:
因为都在圆上
所求圆的方程为
例2 的三个顶点的坐标分别是求它的外接圆的方程.
典例剖析
解法1:设圆心C的坐标为.
因为圆心C在直线上,所以.①
因为是圆上两点,所以|.
根据两点间距离公式,有,即.②
由①②可得.
所以圆心C的坐标是.圆的半径.
所以,所求圆的标准方程是.
例3 已知圆心为C的圆经过两点,且圆心C在直线上,求此圆的
标准方程.
典例剖析
【分析】设圆心C的坐标为.由已知条件可知,|,且.由此可求出圆心坐标和半径.
另外,因为线段是圆的一条弦,根据平面几何知识,的中点与圆心的连线垂直于,由此可得到另一种解法.
待定系数法
解法2:如图,设线段AB的中点为.
由两点的坐标为
可得点的坐标为直线的斜率为.
因此,线段的垂直平分线l′的方程是,即.
由垂径定理可知,圆心也在线段的垂直平分线上,
所以它的坐标是方程组的解.解这个方程组,得
所以圆心C的坐标是.圆的半径.
所以,所求圆的标准方程是.
例3 已知圆心为C的圆经过两点,且圆心C在直线上,求此圆的
标准方程.
典例剖析
几何性质法
归纳总结 圆的标准方程的两种求法
(1)几何法
它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
跟踪训练 已知的顶点坐标分别是 求外接圆的方程.
求出圆的圆心和半径
课堂小结
谢 谢!
