2.3.3点到直线的距离公式 2.3.4两条平行直线间的距离 课件(共19页)
文档属性
| 名称 | 2.3.3点到直线的距离公式 2.3.4两条平行直线间的距离 课件(共19页) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
2.3.3 点到直线的距离公式
2.3.4 两条平行直线间距离公式
第二章
2.3
直线的交点坐标与距离公式
学习目标
1.探索并掌握点到直线的距离公式.
2.会求两平行直线间的距离
3.能根据点到直线的距离公式和两平行直线间的距离公式解决相关问题.
核心素养:数学抽象、数学运算、逻辑推理
思考:如何求出?
探究:已知点,直线.如何求点到直线的距离?
新知学习
点到直线的距离,是指从点到直线的垂线段的长度,其中是垂足(如图所示).
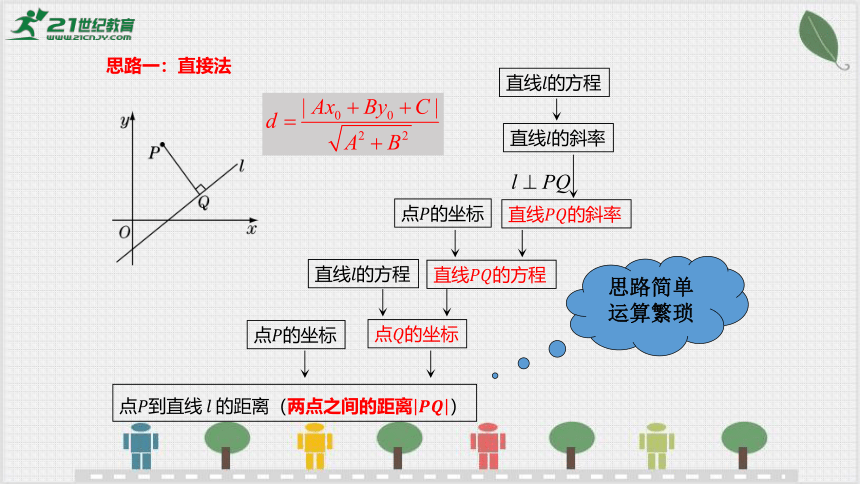
思路一:直接法
直线的方程
直线的斜率
直线的方程
直线的方程
点到直线的距离(两点之间的距离)
点的坐标
直线的斜率
点的坐标
点的坐标
思路简单运算繁琐
探究 我们知道,向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
如图所示,点到直线的距离,就是向量的模.
设是直线上的任意一点,是与直线的方向向量垂直的单位向量,则是在上的投影向量,
||=|·|.
思考 如何利用直线的方程得到与的方向向量垂直的单位向量?
探究 我们知道,向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
||=|·|
思考 如何利用直线的方程得到与的方向向量垂直的单位向量?
取
设是直线 上的任意两点,
是直线 的方向向量
把两式相减,
得.
向量与向量垂直.
向量就是与直线的方向向量垂直的一个单位向量.
·
=||=|·|
思路二:向量法
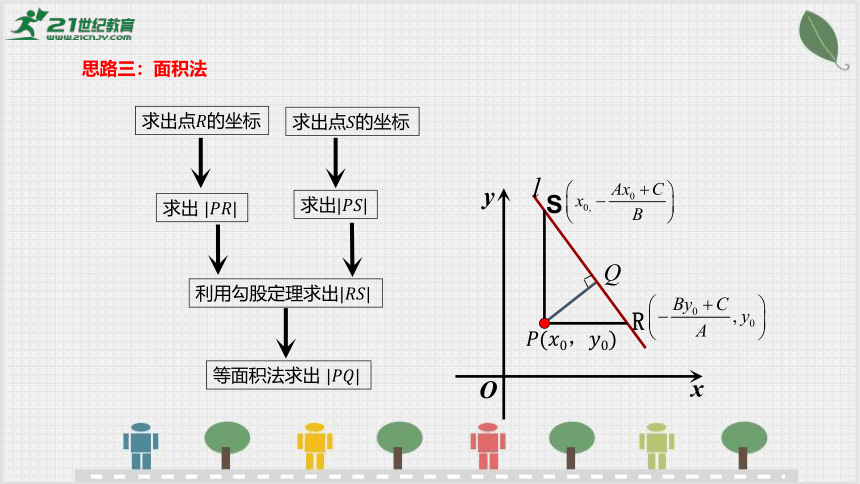
思路三:面积法
x
y
O
等面积法求出
求出
求出
利用勾股定理求出
S
R
求出点的坐标
求出点的坐标
(1) 当A=0或B=0时,公式也成立;
说明:
(2) 直线的方程要化成一般式.
点,直线的距离
例1 求点到下列直线的距离:
(1); (2).
解: (1)根据点到直线的距离公式,得
(2)如图,直线
O
y
x
l:3x=2
P(-1,2)
典例剖析
即平行于轴,
2.求点到直线的距离.
1.求点到直线的距离.
3.点到直线的距离是.
跟踪训练
解:设边上的高为
的方程为
x
y
C
O
-1
1
2
2
3
3
1
B (3,1)
A (1,3)
还有其他方法吗?
例2 已知点,求三角形的面积.
两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
方法一:求两条平行直线间的距离可转化为点到直线的距离;
两条平行线与
之间的距离是
方法二:利用两条平行直线间的距离公式.
新知讲解
两平行直线间的距离:
思考:已知两条平行直线的方程,如何求与间的距离?
(2) 两直线方程中要求的系数要相同.
(1) 把直线方程要化成一般式;
说明:
证明:两条平行线与之间的距离是
证明:在直线上任取一点
点到直线的距离就是这两条平行直线间的距离,
因为点在直线上,所以,
即,
例3 已知两条平行直线 , ,求 l1与 l2 间的距离.
典例剖析
解:(方法一)先求与轴的交点的坐标.
容易知道,点的坐标为.
点到直线的距离
(方法二)直线 可化为
如何取点,可使计算简单?
由两条平行直线间的距离得
1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;
2.两平行线3x+4y=10和6x+8y=0的距离是____.
2
跟踪训练
例4 求与直线平行,且到的距离为2的直线的方程.
解:设所求直线方程为
所求直线为.
即,解得.
3.求经过两直线的交点,且和点A(-3,1)的距离为5的直线的方程.
1.若直线平行,则与之间的距离为( )
A. B. C. D.
2.与直线平行且到的距离等于的直线方程为 ( )
A. B.
C. D.
随堂小测
B
D
1.点到直线的距离公式
2.两条平行直线间的距离公式
两条平行线的距离:
点到直线直线的距离:
课堂小结
谢 谢!
2.3.3 点到直线的距离公式
2.3.4 两条平行直线间距离公式
第二章
2.3
直线的交点坐标与距离公式
学习目标
1.探索并掌握点到直线的距离公式.
2.会求两平行直线间的距离
3.能根据点到直线的距离公式和两平行直线间的距离公式解决相关问题.
核心素养:数学抽象、数学运算、逻辑推理
思考:如何求出?
探究:已知点,直线.如何求点到直线的距离?
新知学习
点到直线的距离,是指从点到直线的垂线段的长度,其中是垂足(如图所示).
思路一:直接法
直线的方程
直线的斜率
直线的方程
直线的方程
点到直线的距离(两点之间的距离)
点的坐标
直线的斜率
点的坐标
点的坐标
思路简单运算繁琐
探究 我们知道,向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
如图所示,点到直线的距离,就是向量的模.
设是直线上的任意一点,是与直线的方向向量垂直的单位向量,则是在上的投影向量,
||=|·|.
思考 如何利用直线的方程得到与的方向向量垂直的单位向量?
探究 我们知道,向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
||=|·|
思考 如何利用直线的方程得到与的方向向量垂直的单位向量?
取
设是直线 上的任意两点,
是直线 的方向向量
把两式相减,
得.
向量与向量垂直.
向量就是与直线的方向向量垂直的一个单位向量.
·
=||=|·|
思路二:向量法
思路三:面积法
x
y
O
等面积法求出
求出
求出
利用勾股定理求出
S
R
求出点的坐标
求出点的坐标
(1) 当A=0或B=0时,公式也成立;
说明:
(2) 直线的方程要化成一般式.
点,直线的距离
例1 求点到下列直线的距离:
(1); (2).
解: (1)根据点到直线的距离公式,得
(2)如图,直线
O
y
x
l:3x=2
P(-1,2)
典例剖析
即平行于轴,
2.求点到直线的距离.
1.求点到直线的距离.
3.点到直线的距离是.
跟踪训练
解:设边上的高为
的方程为
x
y
C
O
-1
1
2
2
3
3
1
B (3,1)
A (1,3)
还有其他方法吗?
例2 已知点,求三角形的面积.
两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
方法一:求两条平行直线间的距离可转化为点到直线的距离;
两条平行线与
之间的距离是
方法二:利用两条平行直线间的距离公式.
新知讲解
两平行直线间的距离:
思考:已知两条平行直线的方程,如何求与间的距离?
(2) 两直线方程中要求的系数要相同.
(1) 把直线方程要化成一般式;
说明:
证明:两条平行线与之间的距离是
证明:在直线上任取一点
点到直线的距离就是这两条平行直线间的距离,
因为点在直线上,所以,
即,
例3 已知两条平行直线 , ,求 l1与 l2 间的距离.
典例剖析
解:(方法一)先求与轴的交点的坐标.
容易知道,点的坐标为.
点到直线的距离
(方法二)直线 可化为
如何取点,可使计算简单?
由两条平行直线间的距离得
1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;
2.两平行线3x+4y=10和6x+8y=0的距离是____.
2
跟踪训练
例4 求与直线平行,且到的距离为2的直线的方程.
解:设所求直线方程为
所求直线为.
即,解得.
3.求经过两直线的交点,且和点A(-3,1)的距离为5的直线的方程.
1.若直线平行,则与之间的距离为( )
A. B. C. D.
2.与直线平行且到的距离等于的直线方程为 ( )
A. B.
C. D.
随堂小测
B
D
1.点到直线的距离公式
2.两条平行直线间的距离公式
两条平行线的距离:
点到直线直线的距离:
课堂小结
谢 谢!
