2.5.2圆与圆位置关系 课件(共17页)
文档属性
| 名称 | 2.5.2圆与圆位置关系 课件(共17页) |  | |
| 格式 | pptx | ||
| 文件大小 | 700.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 08:47:00 | ||
图片预览





文档简介
(共17张PPT)
2.5
直线与圆、圆与圆的位置关系
第二章
2.5.2圆与圆的位置关系
学习目标
1.理解圆与圆的位置关系的种类.
2.掌握圆与圆的位置关系的代数判断方法与几何判断方法.
3.能够利用上述方法判断两圆的位置关系.
4.体会根据圆的对称性灵活处理问题的方法和它的优越性.
核心素养:逻辑推理、数学建模
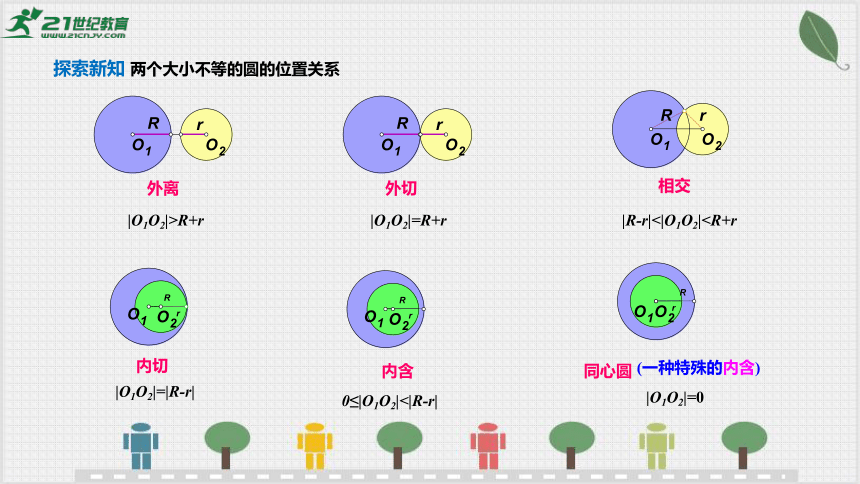
外离
探索新知 两个大小不等的圆的位置关系
|O1O2|>R+r
|O1O2|=R+r
|R-r|<|O1O2||O1O2|=|R-r|
0≤|O1O2|<|R-r|
|O1O2|=0
外切
相交
内切
内含
同心圆
(一种特殊的内含)
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
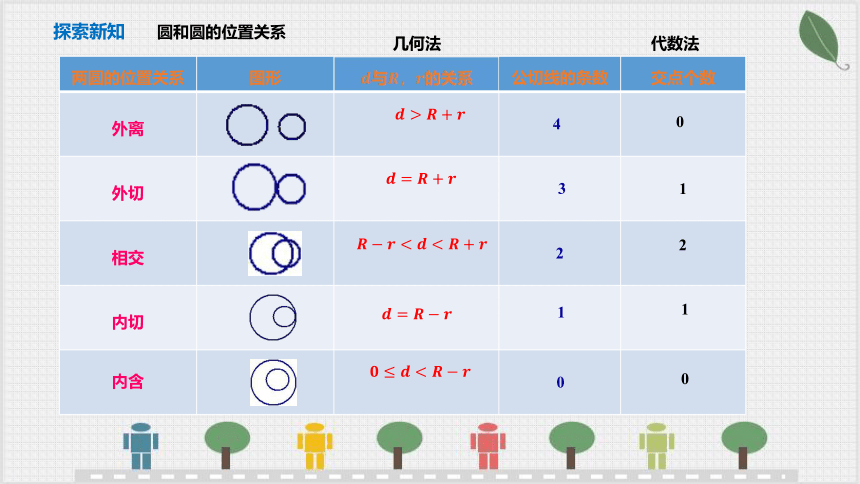
探索新知 圆和圆的位置关系
几何法
代数法
两圆的位置关系 图形 与的关系 公切线的条数 交点个数
外离
内切
外切
内含
相交
2
4
3
0
1
1
0
2
1
0
2和的半径分别为3cm 和 5 cm ,
当时,两圆的位置关是_______.
当时,两圆的位置关是_______.
当时,两圆的位置关是_______.
1.两圆有两个交点,则两圆的位置关系是______.
两圆没有交点,则两圆的位置关系是__________.
两圆只有一个交点,则两圆的位置关系是_________.
相交
外离或内含
内切或外切
外切
内切
外离
即时巩固
例1 已知圆和圆,试判断圆与圆的位置关系.
解法一:圆与圆的方程联立,得
(1)-(2),得
所以,方程(4)有两个不相等的实数根,
因此圆与圆有两个不同的公共点.
所以圆与圆相交,它们有两个公共点.
⑶
判断两圆位置关系的方法
典例剖析
解法二:
把圆C1和圆C2的方程化为标准方程:
∴ 圆与圆相交,它们有两个公共点.
例1 已知圆和圆,试判断圆与圆的位置关系.
判断两圆位置关系的方法
典例剖析
解惑提高 研究两圆的位置关系可以有两种方法
(2)几何法:判断圆心距与两圆半径的和与差的绝对值的大小关系.
(1)代数法:联立两者方程看是否有解.
代数法判断两圆的位置关系的一般步骤
(1)把两圆的方程联立成方程组;
(2)消去y(或x)得到关于x(或y)的一元二次方程;
(3)求出△;
(4)判断△的符号,得出结论:
①若△<0,则两圆内含或外离;
②若△=0,则两圆内切或外切;
③若△>0,则两圆相交.
几何法判断两圆的位置关系的一般步骤
(1)把两圆的方程化成标准方程;
(2)求出两圆的圆心坐标及半径;
(3)求两圆的圆心距;
(4)比较与,的大小关系,得出结论:
①若,则两圆外离;
②若,则两圆外切;
③若,则两圆相交;
④若,则两圆内切;
⑤若,则两圆内含.
思考 判断两圆的位置关系,代数法与几何法有哪些优缺点,如何选用?
代数法能求出两圆的交点,但当△<0或△=0,不能判断出两圆的确切的位置关系;
几何法直观,能够准确判断两圆的位置关系,但不能求出两圆的交点.
1.已知圆,圆,试判断圆与圆的位置关系.
相交
2.点在圆心为的圆上,点在圆心为的圆上,求 的最大值.
y
x
O
M
N
C1
C2
解:把圆的方程都化成标准形式,为
如图,的坐标是,半径是3;
的坐标是,半径是2;
因此, 的最大值是.
即时巩固
例1 设圆圆,
试判断圆与圆的关系.
A
B
y
x
2.你发现了什么?你能说明什么吗?
先动手后动脑
1.画出两圆的图象和方程表示的直线的图象
探索新知
理论迁移
1.求两圆的公共弦所在的直线方程.
2.求以两圆公共弦为直径的圆方程.
3.求过两圆交点且面积最小的圆方程.
例1 设圆,圆,试判断圆与圆的关系.
例2 已知圆O的直径AB=4,动点与点A的距离是它与点B的距离的.试探究点的轨迹,并判断该轨迹与圆O的位置关系.
求动点的轨迹方程
分析:我们可以通过建立适当的平面直角坐标系,求得满足条件的动点M的轨迹方程,从而得到点M的轨迹;通过研究它的轨迹方程与圆O方程的关系,判断这个轨迹与圆O的位置关系.
解:如图,以线段AB的中点O为原点, AB所在直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系.
由AB=4,得A(-2,0),B(2,0).
设点M的坐标为(x,y),由|MA|=|MB|,得
化简,得x2-12x+y2+4=0,即(x-6)2+y2=32
所以点M的轨迹是以P(6,0)为圆心,半径为4的一个圆.
因为两圆的圆心距为|PO|=6,两圆的半径分别为r1=2, r2=4,
所以r1 +r2 <|PO|< r1 +r2,
所以点M的轨迹与圆相交.
第一步:建立坐标系,用坐标和方程表示有关的量.
第二步:进行有关代数运算
第三步:把代数运算结果翻译成几何关系.
——坐标法
x
y
M
A
B
O
.
.
P
典例剖析
解惑提高 坐标法解决平面几何问题的“三步曲”:
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
第一步 :建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为
代数问题;
1.圆和圆的位置关系及其对应的数量关系
(1)两圆外离
(2)两圆外切
(3)两圆相交
(4)两圆内切
(5)两圆内含
2.坐标法解决平面几何问题的“三步曲”
课堂小结
谢 谢!
2.5
直线与圆、圆与圆的位置关系
第二章
2.5.2圆与圆的位置关系
学习目标
1.理解圆与圆的位置关系的种类.
2.掌握圆与圆的位置关系的代数判断方法与几何判断方法.
3.能够利用上述方法判断两圆的位置关系.
4.体会根据圆的对称性灵活处理问题的方法和它的优越性.
核心素养:逻辑推理、数学建模
外离
探索新知 两个大小不等的圆的位置关系
|O1O2|>R+r
|O1O2|=R+r
|R-r|<|O1O2|
0≤|O1O2|<|R-r|
|O1O2|=0
外切
相交
内切
内含
同心圆
(一种特殊的内含)
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
探索新知 圆和圆的位置关系
几何法
代数法
两圆的位置关系 图形 与的关系 公切线的条数 交点个数
外离
内切
外切
内含
相交
2
4
3
0
1
1
0
2
1
0
2和的半径分别为3cm 和 5 cm ,
当时,两圆的位置关是_______.
当时,两圆的位置关是_______.
当时,两圆的位置关是_______.
1.两圆有两个交点,则两圆的位置关系是______.
两圆没有交点,则两圆的位置关系是__________.
两圆只有一个交点,则两圆的位置关系是_________.
相交
外离或内含
内切或外切
外切
内切
外离
即时巩固
例1 已知圆和圆,试判断圆与圆的位置关系.
解法一:圆与圆的方程联立,得
(1)-(2),得
所以,方程(4)有两个不相等的实数根,
因此圆与圆有两个不同的公共点.
所以圆与圆相交,它们有两个公共点.
⑶
判断两圆位置关系的方法
典例剖析
解法二:
把圆C1和圆C2的方程化为标准方程:
∴ 圆与圆相交,它们有两个公共点.
例1 已知圆和圆,试判断圆与圆的位置关系.
判断两圆位置关系的方法
典例剖析
解惑提高 研究两圆的位置关系可以有两种方法
(2)几何法:判断圆心距与两圆半径的和与差的绝对值的大小关系.
(1)代数法:联立两者方程看是否有解.
代数法判断两圆的位置关系的一般步骤
(1)把两圆的方程联立成方程组;
(2)消去y(或x)得到关于x(或y)的一元二次方程;
(3)求出△;
(4)判断△的符号,得出结论:
①若△<0,则两圆内含或外离;
②若△=0,则两圆内切或外切;
③若△>0,则两圆相交.
几何法判断两圆的位置关系的一般步骤
(1)把两圆的方程化成标准方程;
(2)求出两圆的圆心坐标及半径;
(3)求两圆的圆心距;
(4)比较与,的大小关系,得出结论:
①若,则两圆外离;
②若,则两圆外切;
③若,则两圆相交;
④若,则两圆内切;
⑤若,则两圆内含.
思考 判断两圆的位置关系,代数法与几何法有哪些优缺点,如何选用?
代数法能求出两圆的交点,但当△<0或△=0,不能判断出两圆的确切的位置关系;
几何法直观,能够准确判断两圆的位置关系,但不能求出两圆的交点.
1.已知圆,圆,试判断圆与圆的位置关系.
相交
2.点在圆心为的圆上,点在圆心为的圆上,求 的最大值.
y
x
O
M
N
C1
C2
解:把圆的方程都化成标准形式,为
如图,的坐标是,半径是3;
的坐标是,半径是2;
因此, 的最大值是.
即时巩固
例1 设圆圆,
试判断圆与圆的关系.
A
B
y
x
2.你发现了什么?你能说明什么吗?
先动手后动脑
1.画出两圆的图象和方程表示的直线的图象
探索新知
理论迁移
1.求两圆的公共弦所在的直线方程.
2.求以两圆公共弦为直径的圆方程.
3.求过两圆交点且面积最小的圆方程.
例1 设圆,圆,试判断圆与圆的关系.
例2 已知圆O的直径AB=4,动点与点A的距离是它与点B的距离的.试探究点的轨迹,并判断该轨迹与圆O的位置关系.
求动点的轨迹方程
分析:我们可以通过建立适当的平面直角坐标系,求得满足条件的动点M的轨迹方程,从而得到点M的轨迹;通过研究它的轨迹方程与圆O方程的关系,判断这个轨迹与圆O的位置关系.
解:如图,以线段AB的中点O为原点, AB所在直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系.
由AB=4,得A(-2,0),B(2,0).
设点M的坐标为(x,y),由|MA|=|MB|,得
化简,得x2-12x+y2+4=0,即(x-6)2+y2=32
所以点M的轨迹是以P(6,0)为圆心,半径为4的一个圆.
因为两圆的圆心距为|PO|=6,两圆的半径分别为r1=2, r2=4,
所以r1 +r2 <|PO|< r1 +r2,
所以点M的轨迹与圆相交.
第一步:建立坐标系,用坐标和方程表示有关的量.
第二步:进行有关代数运算
第三步:把代数运算结果翻译成几何关系.
——坐标法
x
y
M
A
B
O
.
.
P
典例剖析
解惑提高 坐标法解决平面几何问题的“三步曲”:
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
第一步 :建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为
代数问题;
1.圆和圆的位置关系及其对应的数量关系
(1)两圆外离
(2)两圆外切
(3)两圆相交
(4)两圆内切
(5)两圆内含
2.坐标法解决平面几何问题的“三步曲”
课堂小结
谢 谢!
