3.1.1椭圆及其标准方程 课件(共20页)
文档属性
| 名称 | 3.1.1椭圆及其标准方程 课件(共20页) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 08:47:00 | ||
图片预览



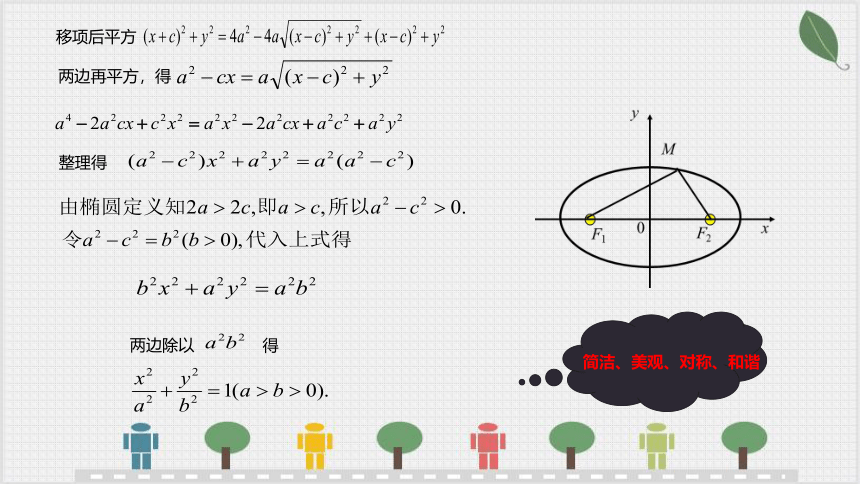
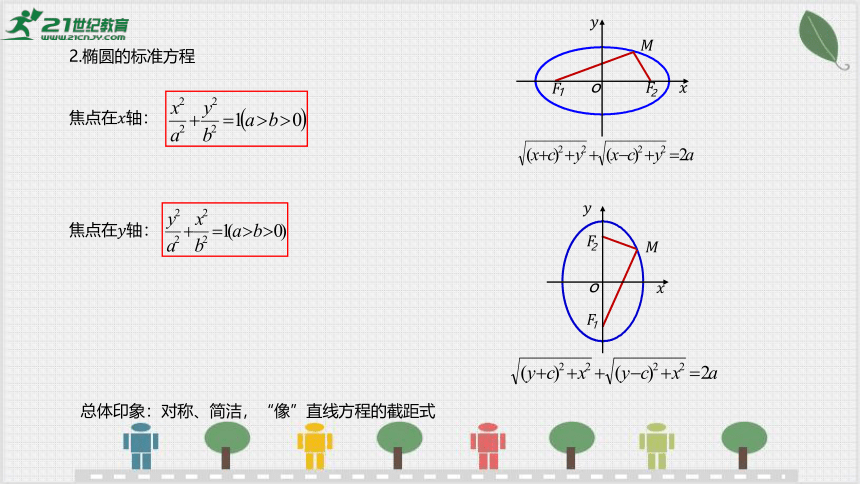

文档简介
(共20张PPT)
3.1
椭圆
第三章
3.1.1 椭圆及其标准方程
学习目标
1.了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用.
2.掌握椭圆的定义和标准方程.
3.会求椭圆的标准方程.
核心素养:数学抽象、数学建模、数学运算
新知学习
1.椭圆的定义
我们把平面内与两个定点的距离的和等于常数(大于 )的点的轨迹叫做椭圆.
这两个定点、叫做椭圆的焦点.两个焦点的距离叫做焦距.
注意 椭圆定义中容易遗漏的地方:
(1)两个定点间的距离
(2)与两个定点的距离的和等于常数
(3)
焦距的一半称为半焦距.
新知学习
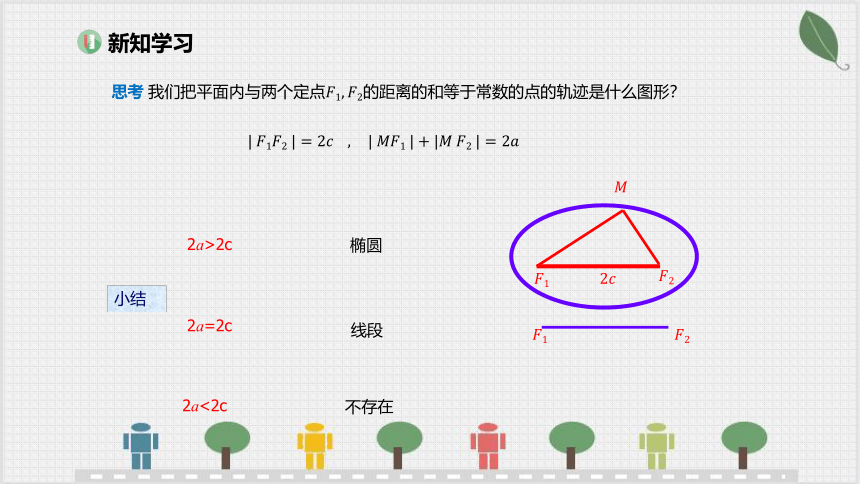
思考 我们把平面内与两个定点的距离的和等于常数的点的轨迹是什么图形?
2a>2c
2a=2c
2a<2c
小结
椭圆
线段
不存在
新知学习
回忆如何求圆的方程
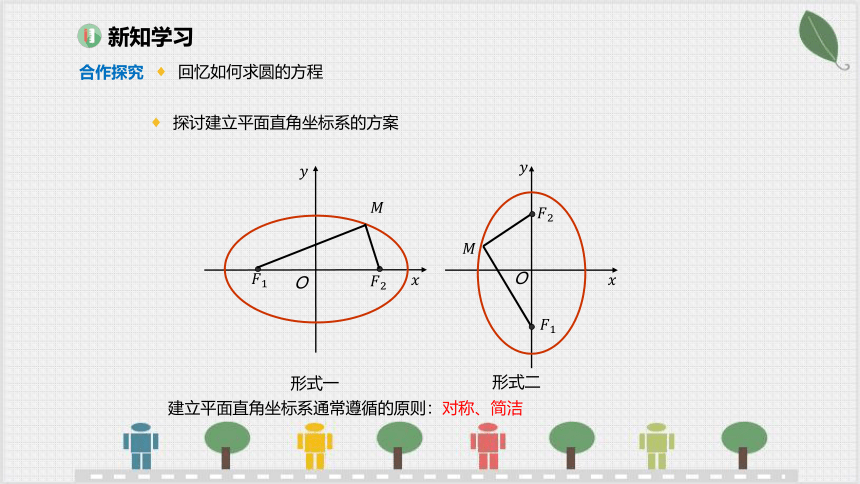
探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:对称、简洁
O
形式一
形式二
O
合作探究
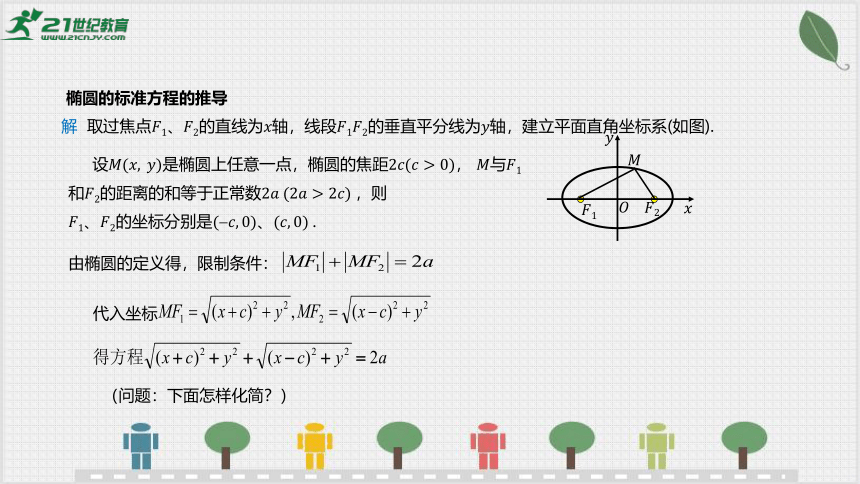
解 取过焦点的直线为轴,线段的垂直平分线为轴,建立平面直角坐标系(如图).
设是椭圆上任意一点,椭圆的焦距, 与和的距离的和等于正常数,则
的坐标分别是.
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标
椭圆的标准方程的推导
整理得
两边再平方,得
移项后平方
得
两边除以
简洁、美观、对称、和谐
总体印象:对称、简洁,“像”直线方程的截距式
焦点在轴:
焦点在轴:
2.椭圆的标准方程
1
o
2
1
2
o
[1]建系设点
[2]列等式
[3]等式坐标化
[4]化简
[5]证明
求椭圆的方程方法——坐标法
归纳总结
图 形
方 程
焦 点
之间
的关系
定 义
1
2
o
F
F
M
1
o
2
两类标准方程的对照表
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
图 形
方 程
1
2
y
o
F
F
x
1
o
F
y
x
2
F
1.判定下列椭圆的焦点在哪个轴,并指明,写出焦点坐标
答:在 x 轴.(-3,0)和(3,0)
答:在 轴.(0,-5)和(0,5)
答:在轴.(0,-1)和(0,1)
反思感悟 判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上.
及时巩固
2.将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标
反思感悟 在下述方程中,满足什么条件,就表示椭圆?
答同号,且不等于.
(1) 两个焦点的坐标分别是(-4,0),(4,0),椭圆上一点到两焦点距离的和等于10.
例1 写出适合下列条件的椭圆的标准方程:
解 因为焦点在x轴上,所以设它的标准方程为
求椭圆的标准方程
(2) 求两个焦点的坐标分别是(0,-2),(0,2),并且经过点 的椭圆方程.
解 因为焦点在y轴上,所以设它的标准方程为:
法1:
由题意得:
解得:
例1 写出适合下列条件的椭圆的标准方程
法2:
(2) 求两个焦点的坐标分别是(0,-2),(0,2),并且经过点 的椭圆方程.
例1 写出适合下列条件的椭圆的标准方程
(3) 求经过两点 (3,),(,-2)的椭圆方程.
例1 写出适合下列条件的椭圆的标准方程
解 设椭圆的方程为:
∴
解得:
∴所求椭圆的方程为:
=1
反思感悟
1 椭圆 上一点到一个焦点的距离为5,则 到另一个焦点的距离为( )
A.5 B.6 C.4 D.10
A
2.已知椭圆的方程为 ,焦点在轴上,则其焦距为( )
A
3. ,焦点在y轴上的椭圆的标准方程是 __________.
随堂自测
(1)椭圆的定义
(2)椭圆的标准方程
焦点在x轴:
焦点在y轴:
(3)求椭圆的标准方程的方法
代定系数法
定义法
课堂小结
3.1
椭圆
第三章
3.1.1 椭圆及其标准方程
学习目标
1.了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用.
2.掌握椭圆的定义和标准方程.
3.会求椭圆的标准方程.
核心素养:数学抽象、数学建模、数学运算
新知学习
1.椭圆的定义
我们把平面内与两个定点的距离的和等于常数(大于 )的点的轨迹叫做椭圆.
这两个定点、叫做椭圆的焦点.两个焦点的距离叫做焦距.
注意 椭圆定义中容易遗漏的地方:
(1)两个定点间的距离
(2)与两个定点的距离的和等于常数
(3)
焦距的一半称为半焦距.
新知学习
思考 我们把平面内与两个定点的距离的和等于常数的点的轨迹是什么图形?
2a>2c
2a=2c
2a<2c
小结
椭圆
线段
不存在
新知学习
回忆如何求圆的方程
探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:对称、简洁
O
形式一
形式二
O
合作探究
解 取过焦点的直线为轴,线段的垂直平分线为轴,建立平面直角坐标系(如图).
设是椭圆上任意一点,椭圆的焦距, 与和的距离的和等于正常数,则
的坐标分别是.
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标
椭圆的标准方程的推导
整理得
两边再平方,得
移项后平方
得
两边除以
简洁、美观、对称、和谐
总体印象:对称、简洁,“像”直线方程的截距式
焦点在轴:
焦点在轴:
2.椭圆的标准方程
1
o
2
1
2
o
[1]建系设点
[2]列等式
[3]等式坐标化
[4]化简
[5]证明
求椭圆的方程方法——坐标法
归纳总结
图 形
方 程
焦 点
之间
的关系
定 义
1
2
o
F
F
M
1
o
2
两类标准方程的对照表
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
图 形
方 程
1
2
y
o
F
F
x
1
o
F
y
x
2
F
1.判定下列椭圆的焦点在哪个轴,并指明,写出焦点坐标
答:在 x 轴.(-3,0)和(3,0)
答:在 轴.(0,-5)和(0,5)
答:在轴.(0,-1)和(0,1)
反思感悟 判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上.
及时巩固
2.将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标
反思感悟 在下述方程中,满足什么条件,就表示椭圆?
答同号,且不等于.
(1) 两个焦点的坐标分别是(-4,0),(4,0),椭圆上一点到两焦点距离的和等于10.
例1 写出适合下列条件的椭圆的标准方程:
解 因为焦点在x轴上,所以设它的标准方程为
求椭圆的标准方程
(2) 求两个焦点的坐标分别是(0,-2),(0,2),并且经过点 的椭圆方程.
解 因为焦点在y轴上,所以设它的标准方程为:
法1:
由题意得:
解得:
例1 写出适合下列条件的椭圆的标准方程
法2:
(2) 求两个焦点的坐标分别是(0,-2),(0,2),并且经过点 的椭圆方程.
例1 写出适合下列条件的椭圆的标准方程
(3) 求经过两点 (3,),(,-2)的椭圆方程.
例1 写出适合下列条件的椭圆的标准方程
解 设椭圆的方程为:
∴
解得:
∴所求椭圆的方程为:
=1
反思感悟
1 椭圆 上一点到一个焦点的距离为5,则 到另一个焦点的距离为( )
A.5 B.6 C.4 D.10
A
2.已知椭圆的方程为 ,焦点在轴上,则其焦距为( )
A
3. ,焦点在y轴上的椭圆的标准方程是 __________.
随堂自测
(1)椭圆的定义
(2)椭圆的标准方程
焦点在x轴:
焦点在y轴:
(3)求椭圆的标准方程的方法
代定系数法
定义法
课堂小结
