3.2.2双曲线的简单几何性质 课件(共24页)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质 课件(共24页) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 08:47:00 | ||
图片预览





文档简介
(共24张PPT)
3.2
双曲线
第三章
3.2.2 双曲线的简单几何性质
学习目标
1.理解双曲线的简单几何性质(范围、对称性、顶点、渐近线、离心率).
2.能用双曲线的简单性质解决一些简单的问题
核心素养:数学运算、数学建模
复习引入
新知学习
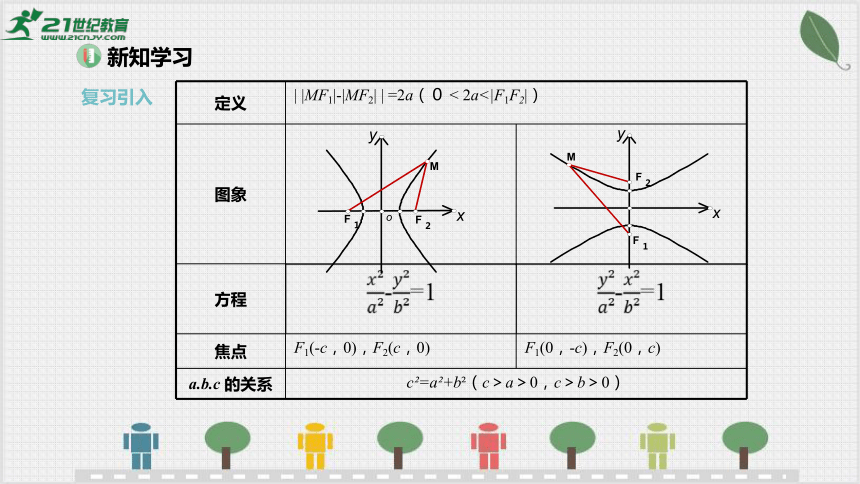
定义 | |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
图象
方程 -=1 -=1
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
a.b.c 的关系 c =a +b (c>a>0,c>b>0)
2、对称性
1、范围
∵≥1,即x ≥a
∴x≥a,x≤-a
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
新知讲解
一 双曲线-=1(a>0,b>0)的简单几何性质
关于x轴、y轴和坐标原点都对称. x轴、y轴是双曲线
的对称轴,原点是对称中心,又叫做双曲线的中心.
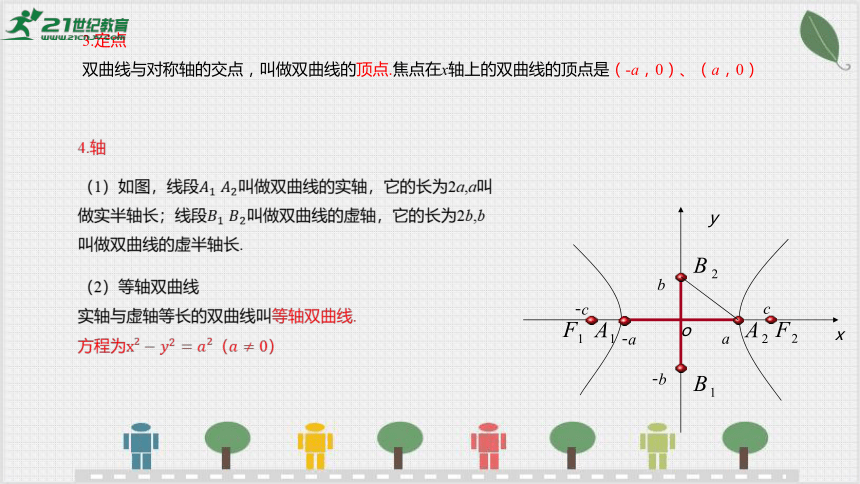
3.定点
双曲线与对称轴的交点,叫做双曲线的顶点.焦点在x轴上的双曲线的顶点是(-a,0)、(a,0)
x
y
o
-b
b
-a
a
4.轴
(1)如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
(2)等轴双曲线
实轴与虚轴等长的双曲线叫等轴双曲线.
方程为
-c
c
M(x,y)
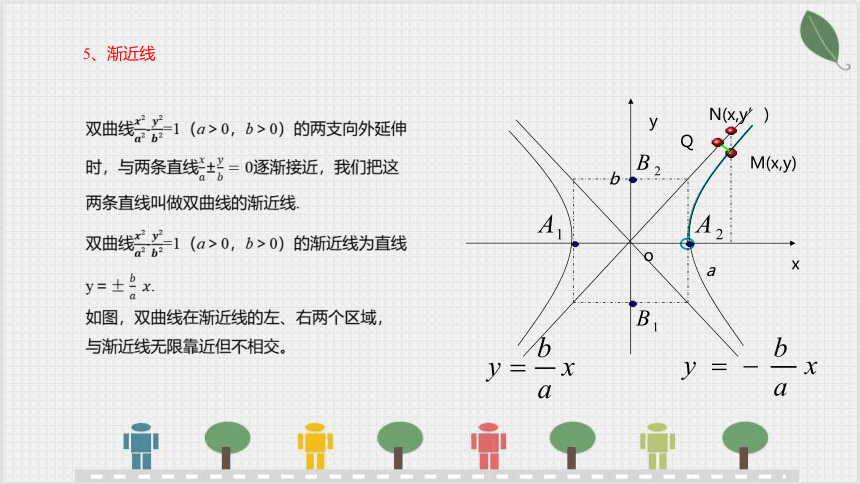
5、渐近线
N(x,y’)
Q
x
y
o
a
b
双曲线-=1(a>0,b>0)的两支向外延伸时,与两条直线±逐渐接近,我们把这两条直线叫做双曲线的渐近线.
双曲线-=1(a>0,b>0)的渐近线为直线y=.
如图,双曲线在渐近线的左、右两个区域,与渐近线无限靠近但不相交。
6、离心率
(1)定义:与椭圆类似,双曲线的焦距与实轴长的比 ,叫做双曲线的离心率.
(2)e的范围:因为c>a>0,所以双曲线的离心率e>1.
(3)e的含义:e是表示双曲线开口大小的一个量,e越大开口越大.
(4)等轴双曲线的离心率e=,即离心率e=是等轴双曲线
(5),在a,b,c,e四个参数中,知二可求二
x
y
o
-a
a
b
-b
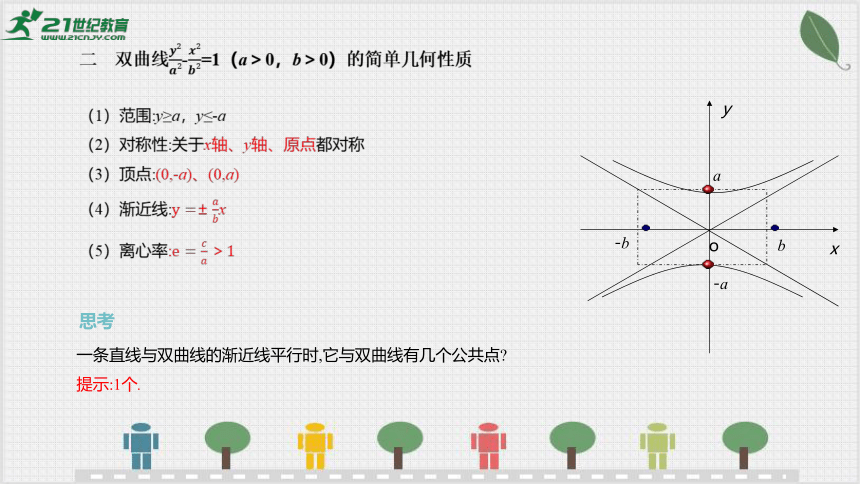
(1)范围:y≥a,y≤-a
(2)对称性:关于x轴、y轴、原点都对称
(3)顶点:(0,-a)、(0,a)
(4)渐近线:x
(5)离心率:
二 双曲线-=1(a>0,b>0)的简单几何性质
一条直线与双曲线的渐近线平行时,它与双曲线有几个公共点
提示:1个.
思考
1. 若双曲线的渐近线方程为则双曲线的离心率为 .
2、若双曲线的离心率为2,则两条渐近线的方程为 .
即时巩固
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实、虚轴 长、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0a,b,c关系 a2+b2=c2 a2-b2=c2
三 双曲线与椭圆的区别
一、已知双曲线的方程求其几何性质
例1 求双曲线9y -16x =144的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程.
解 把方程化为标准方程
,虚半轴长b=3,
半焦距c=,
焦点坐标是(0,-5),(0,5),
离心率=,
渐近线方程为.
典例剖析
反思感悟
由双曲线方程研究双曲线的几何性质,关键是求出a,b,c的值,如果已知方程不是标准方程,首先要化为标准方程,利用焦点在x2,y2两项中系数为正的坐标轴上可判断焦点的位置,利用焦点一定在实轴上确定a,b的值,再利用c2=a2+b2确定c的值.
跟踪训练 双曲线x2-my2=1的实轴长是虚轴长的2倍,则m等于 (D)
A. B. C.2 D.4
二、求双曲线方程
反思感悟 1.待定系数法求双曲线的标准方程
具体过程是先定形 ,再定量.即先确定双曲线标准方程的形式,然后再根据a,b,c,e及渐近线方程之间的关系,求出a,b的值
2.巧设双曲线方程的六种方法与技巧
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
跟踪训练 求适合下列条件的双曲线的标准方程:
(1)焦点在x轴上,虚轴长为8,离心率为 ;
(2)两顶点间的距离是6,两焦点的连线被两顶点和对称中心四等分;
解 (1)设所求双曲线的标准方程为 -=1(a>0,b>0),则2b=8,e=,
从而b=4,c= a,代入c2=a2+b2,得a2=9,
故双曲线的标准方程为.
(2)由两顶点间的距离是6,得2a=6,即a=3.
由两焦点的连线被两顶点和对称中心四等分,可得2c=4a=12,
即c=6,于是有b2=c2-a2=62-32=27.
由于焦点所在的坐标轴不确定,
故所求双曲线的标准方程为 或 .
三、求双曲线的离心率
例3 若以双曲线 (a>0)的左、右焦点和点(2,)为顶点的三角形为直角三角形,则该双曲线的离心率为 (B)
A. B. C.2 D.
解析 由题意得点(2,)为该直角三角形的直角顶点,双曲线的左、右焦点分别为(-c,0),(c,0),则有=-1,解得c2=6,所以a2=c2-4=2,因此.
反思感悟 双曲线离心率的求法
双曲线的离心率是双曲线最重要的几何性质之一,求双曲线的离心率(或离心率的取值范围)常见的方法有两种:
(1)求出a,c,代入公式e=;
(2)根据已知条件得到关于a,b,c的齐次式,结合b2=c2-a2转化为a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式),解方程(不等式)即可得e(e的取值范围).
跟踪训练 设双曲线C: -=1(a>0,b>0)的左、右焦点分别是F1,F2,过F1的直线与双曲线C的左支交于M,N两点,若|MF2|=|F1F2|,且2|MF1|=|NF1|,则双曲线的离心率是 ( D )
A.2 B. C. D.
解析 解析:如图所示,取F1M的中点P,则|MF2|=|F1F2|=2c,|MP|=c-a,|F1P|=c-a.
又|NF1|=2|MF1|,∴ |NF1|=4(c-a),|NF2|=4c-2a.
在Rt△NPF2中,|NP|2+|PF2|2=|NF2|2;
在Rt△MPF2中,|MP|2+|PF2|2=|MF2|2.
整理得(4c-2a)2-[5(c-a)]2=(2c)2-(c-a)2,
化简得3c2-8ac+5a2=0,即(c-a)(3c-5a)=0,
得c=a(舍去)或3c=5a,∴ e .
四、双曲线的实际应用
例4 双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(图(1)).它的最小半径为12 m,上口半径为13 m,下口半径为25 m,高为55 m.试建立适当的坐标系,求出此双曲线的方程(精确到1 m).
图(1)
解 根据双曲线的对称性,在冷却塔的轴截面所在平面建立如有图所示的直角坐标系Oxy,使小圆的直径AA′在x轴上,圆心与原点重合.这时,上、下口的直径CC′,BB′都平行于x轴,且|CC′|=13×2,|BB′|=25×2.
设双曲线的方程为 -=1(a>0,b>0),点C的坐标为(13,y),则点B的坐标为(25,y-55).
因为直径AA′是实轴,所以a=12.又B,C两点都在双曲线上,所以
由方程②,得y=(负值舍去).代入方程①,得 - =1.
化简得19b2+275b-18 150=0. ③
解方程③,得b≈25(负值舍去).
因此所求双曲线的方程为 =1.
随堂小测
C
D
B
或
或
关于坐标轴和
原点
都对称
性质
双曲线
范围
对称性
顶点
渐近线
离心率
图象
课堂小结
3.2
双曲线
第三章
3.2.2 双曲线的简单几何性质
学习目标
1.理解双曲线的简单几何性质(范围、对称性、顶点、渐近线、离心率).
2.能用双曲线的简单性质解决一些简单的问题
核心素养:数学运算、数学建模
复习引入
新知学习
定义 | |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
图象
方程 -=1 -=1
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
a.b.c 的关系 c =a +b (c>a>0,c>b>0)
2、对称性
1、范围
∵≥1,即x ≥a
∴x≥a,x≤-a
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
新知讲解
一 双曲线-=1(a>0,b>0)的简单几何性质
关于x轴、y轴和坐标原点都对称. x轴、y轴是双曲线
的对称轴,原点是对称中心,又叫做双曲线的中心.
3.定点
双曲线与对称轴的交点,叫做双曲线的顶点.焦点在x轴上的双曲线的顶点是(-a,0)、(a,0)
x
y
o
-b
b
-a
a
4.轴
(1)如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
(2)等轴双曲线
实轴与虚轴等长的双曲线叫等轴双曲线.
方程为
-c
c
M(x,y)
5、渐近线
N(x,y’)
Q
x
y
o
a
b
双曲线-=1(a>0,b>0)的两支向外延伸时,与两条直线±逐渐接近,我们把这两条直线叫做双曲线的渐近线.
双曲线-=1(a>0,b>0)的渐近线为直线y=.
如图,双曲线在渐近线的左、右两个区域,与渐近线无限靠近但不相交。
6、离心率
(1)定义:与椭圆类似,双曲线的焦距与实轴长的比 ,叫做双曲线的离心率.
(2)e的范围:因为c>a>0,所以双曲线的离心率e>1.
(3)e的含义:e是表示双曲线开口大小的一个量,e越大开口越大.
(4)等轴双曲线的离心率e=,即离心率e=是等轴双曲线
(5),在a,b,c,e四个参数中,知二可求二
x
y
o
-a
a
b
-b
(1)范围:y≥a,y≤-a
(2)对称性:关于x轴、y轴、原点都对称
(3)顶点:(0,-a)、(0,a)
(4)渐近线:x
(5)离心率:
二 双曲线-=1(a>0,b>0)的简单几何性质
一条直线与双曲线的渐近线平行时,它与双曲线有几个公共点
提示:1个.
思考
1. 若双曲线的渐近线方程为则双曲线的离心率为 .
2、若双曲线的离心率为2,则两条渐近线的方程为 .
即时巩固
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实、虚轴 长、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0
三 双曲线与椭圆的区别
一、已知双曲线的方程求其几何性质
例1 求双曲线9y -16x =144的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程.
解 把方程化为标准方程
,虚半轴长b=3,
半焦距c=,
焦点坐标是(0,-5),(0,5),
离心率=,
渐近线方程为.
典例剖析
反思感悟
由双曲线方程研究双曲线的几何性质,关键是求出a,b,c的值,如果已知方程不是标准方程,首先要化为标准方程,利用焦点在x2,y2两项中系数为正的坐标轴上可判断焦点的位置,利用焦点一定在实轴上确定a,b的值,再利用c2=a2+b2确定c的值.
跟踪训练 双曲线x2-my2=1的实轴长是虚轴长的2倍,则m等于 (D)
A. B. C.2 D.4
二、求双曲线方程
反思感悟 1.待定系数法求双曲线的标准方程
具体过程是先定形 ,再定量.即先确定双曲线标准方程的形式,然后再根据a,b,c,e及渐近线方程之间的关系,求出a,b的值
2.巧设双曲线方程的六种方法与技巧
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
跟踪训练 求适合下列条件的双曲线的标准方程:
(1)焦点在x轴上,虚轴长为8,离心率为 ;
(2)两顶点间的距离是6,两焦点的连线被两顶点和对称中心四等分;
解 (1)设所求双曲线的标准方程为 -=1(a>0,b>0),则2b=8,e=,
从而b=4,c= a,代入c2=a2+b2,得a2=9,
故双曲线的标准方程为.
(2)由两顶点间的距离是6,得2a=6,即a=3.
由两焦点的连线被两顶点和对称中心四等分,可得2c=4a=12,
即c=6,于是有b2=c2-a2=62-32=27.
由于焦点所在的坐标轴不确定,
故所求双曲线的标准方程为 或 .
三、求双曲线的离心率
例3 若以双曲线 (a>0)的左、右焦点和点(2,)为顶点的三角形为直角三角形,则该双曲线的离心率为 (B)
A. B. C.2 D.
解析 由题意得点(2,)为该直角三角形的直角顶点,双曲线的左、右焦点分别为(-c,0),(c,0),则有=-1,解得c2=6,所以a2=c2-4=2,因此.
反思感悟 双曲线离心率的求法
双曲线的离心率是双曲线最重要的几何性质之一,求双曲线的离心率(或离心率的取值范围)常见的方法有两种:
(1)求出a,c,代入公式e=;
(2)根据已知条件得到关于a,b,c的齐次式,结合b2=c2-a2转化为a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式),解方程(不等式)即可得e(e的取值范围).
跟踪训练 设双曲线C: -=1(a>0,b>0)的左、右焦点分别是F1,F2,过F1的直线与双曲线C的左支交于M,N两点,若|MF2|=|F1F2|,且2|MF1|=|NF1|,则双曲线的离心率是 ( D )
A.2 B. C. D.
解析 解析:如图所示,取F1M的中点P,则|MF2|=|F1F2|=2c,|MP|=c-a,|F1P|=c-a.
又|NF1|=2|MF1|,∴ |NF1|=4(c-a),|NF2|=4c-2a.
在Rt△NPF2中,|NP|2+|PF2|2=|NF2|2;
在Rt△MPF2中,|MP|2+|PF2|2=|MF2|2.
整理得(4c-2a)2-[5(c-a)]2=(2c)2-(c-a)2,
化简得3c2-8ac+5a2=0,即(c-a)(3c-5a)=0,
得c=a(舍去)或3c=5a,∴ e .
四、双曲线的实际应用
例4 双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(图(1)).它的最小半径为12 m,上口半径为13 m,下口半径为25 m,高为55 m.试建立适当的坐标系,求出此双曲线的方程(精确到1 m).
图(1)
解 根据双曲线的对称性,在冷却塔的轴截面所在平面建立如有图所示的直角坐标系Oxy,使小圆的直径AA′在x轴上,圆心与原点重合.这时,上、下口的直径CC′,BB′都平行于x轴,且|CC′|=13×2,|BB′|=25×2.
设双曲线的方程为 -=1(a>0,b>0),点C的坐标为(13,y),则点B的坐标为(25,y-55).
因为直径AA′是实轴,所以a=12.又B,C两点都在双曲线上,所以
由方程②,得y=(负值舍去).代入方程①,得 - =1.
化简得19b2+275b-18 150=0. ③
解方程③,得b≈25(负值舍去).
因此所求双曲线的方程为 =1.
随堂小测
C
D
B
或
或
关于坐标轴和
原点
都对称
性质
双曲线
范围
对称性
顶点
渐近线
离心率
图象
课堂小结
