青岛版七年级下册9.2平行线和它的画法课件(共21张PPT)
文档属性
| 名称 | 青岛版七年级下册9.2平行线和它的画法课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
情境导入
在同一平面内的两条直线有怎样的位置关系?
9.2平行线和它的画法
1.了解同一平面内两条直线平行的定义
和表示方法.
2.会利用一副三角尺过一点画已知直线
的平行线.
3.掌握平行线的基本性质和它的推论.
学习目标
平行线的概念:
在同一平面内,不相交的两条直线叫做平行线。
B
A
C
D
记作“AB∥CD”,“m//n”,
读作“AB平行于CD”,“m平行于n”.
通常用“//”表示平行,
m
n
如图直线AB与直线CD平行,直线m与直线n平行,
探究新知
1.在同一平面内,两条直线有___种位置关系,
分别是____,如果两条直线a,b不相交,那么
这两条直线的位置关系一定是___,记作___.
2.下列平行的表示方法中规范的是( )
A.a∥CD B.AB∥Cd C.A∥B D.a∥b
3.在同一平面内,下列说法正确的是( )
A、两直线有平行、相交和垂直三种位置关系.
B、不平行的两条直线一定相交.
C、不垂直的两条直线一定平行的.
D、两条射线不相交,则这两条射线平行.
随堂练习
1.在同一个平面内,两条不重合的直线有哪几种位
置关系?
2.判断下列说法是否正确,并说明理由.
①不相交的两条直线是平行线.( )
②在同一平面内,两条不相交的线段是平行线.( )
3.用符号“∥”表示图中平行四边形的两组对边分别平行.
A
B
C
D
相交和平行
×
×
随堂练习
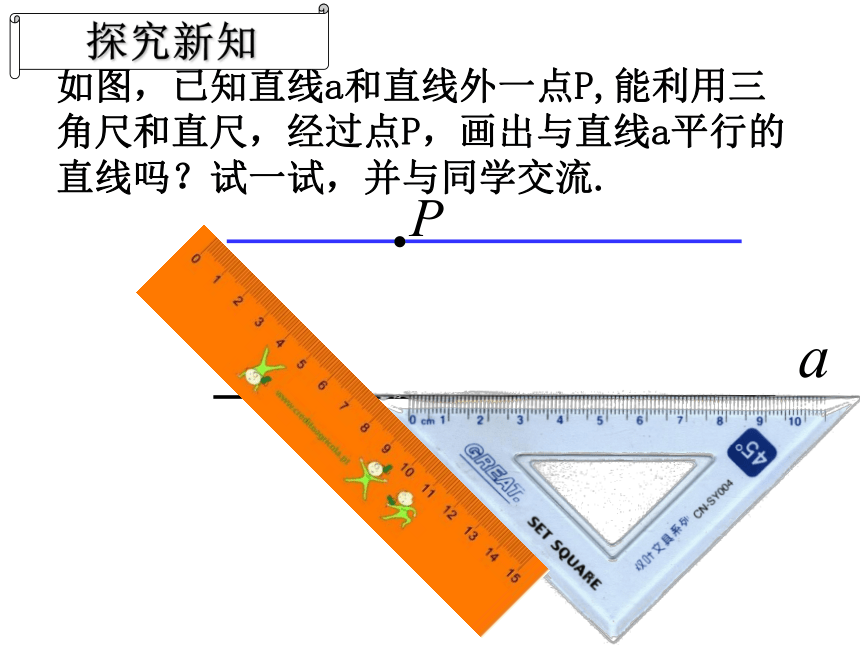
如图,已知直线a和直线外一点p,能利用三角尺和直尺,经过点p,画出与直线a平行的直线吗?试一试,并与同学交流。
a
.P
实验与探究
如图,已知直线a和直线外一点P,能利用三角尺和直尺,经过点P,画出与直线a平行的直线吗?试一试,并与同学交流.
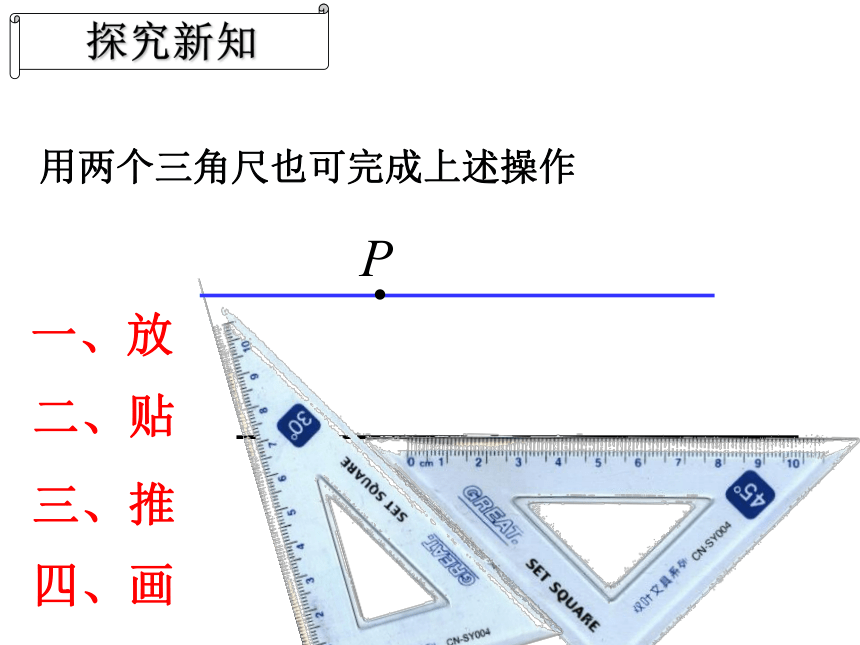
探究新知
一、放
二、贴
三、推
四、画
用两个三角尺也可完成上述操作
探究新知
你能把上面画图的步骤叙述出来吗?
过直线外一点画已知直线的平行线的方法:
①“放”把三角尺的一边放在直线上.
②“贴”用直尺或另一个三角尺紧贴在三角尺
的另一边.
③“推”把第一个三角尺沿直尺边或另一个三
角尺边推到过已知点.
④“画”沿推动后的第一个三角尺边画出直线
探究新知
画一画
1.课本33页 练习 第3题
2.课本34页 习题 第2题
通过上面平行线的画图,你发现经过直线外
一点能作多少条直线与已知直线平行?
平行线的基本性质:
过直线外一点,有且只有一条直线
与这条直线平行.
探究新知
利用平行线的基本性质画图.
已知:直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平
行线平行吗?
如果两条直线都和第三条直线平行,那么这两条直线也相互平行.
平行线基本性质的推论:
简单一点可写成:
平行于同一条直线的两条直线平行.
探究新知
用数学语言表达平行线基本性质的推论:
∵a∥b,a∥c
∴b∥c.
传递性
探究新知
如果直线b//a,c//a,那么直线b//c,即直线b与直线c不相交,你能结合本节课学行线性质解释一下吗?
M
c
b
a
议一议
本节课你学到了哪些知识?
(1)平行线的概念和表示方法;
(2)平行线的画法;
(3)平行线的性质。
小结
1.如图:在
内有一点E,过点E分别画OA、
OB的平行线EC、ED,用符号表示:OA
,
ED
.
A
O
B
D
E
C
//CE
//OB
达标检测
2.判断正误:
(1)在同一平面内,两条不平行的直线是相交线( )
(2)与同一条直线平行的两条直线必平行( )
(3)过直线外一点有且只有一条直线与已知直线平
行( )
√
√
√
3.观察如图所示的正方体并回答.
与AB平行的棱有哪些?
4.如图,过△ABC的顶点分别画对边的平行线,
分别交于D,E,F三点.
习题9.2 : 复习与巩固 1题,2题
作业布置
情境导入
在同一平面内的两条直线有怎样的位置关系?
9.2平行线和它的画法
1.了解同一平面内两条直线平行的定义
和表示方法.
2.会利用一副三角尺过一点画已知直线
的平行线.
3.掌握平行线的基本性质和它的推论.
学习目标
平行线的概念:
在同一平面内,不相交的两条直线叫做平行线。
B
A
C
D
记作“AB∥CD”,“m//n”,
读作“AB平行于CD”,“m平行于n”.
通常用“//”表示平行,
m
n
如图直线AB与直线CD平行,直线m与直线n平行,
探究新知
1.在同一平面内,两条直线有___种位置关系,
分别是____,如果两条直线a,b不相交,那么
这两条直线的位置关系一定是___,记作___.
2.下列平行的表示方法中规范的是( )
A.a∥CD B.AB∥Cd C.A∥B D.a∥b
3.在同一平面内,下列说法正确的是( )
A、两直线有平行、相交和垂直三种位置关系.
B、不平行的两条直线一定相交.
C、不垂直的两条直线一定平行的.
D、两条射线不相交,则这两条射线平行.
随堂练习
1.在同一个平面内,两条不重合的直线有哪几种位
置关系?
2.判断下列说法是否正确,并说明理由.
①不相交的两条直线是平行线.( )
②在同一平面内,两条不相交的线段是平行线.( )
3.用符号“∥”表示图中平行四边形的两组对边分别平行.
A
B
C
D
相交和平行
×
×
随堂练习
如图,已知直线a和直线外一点p,能利用三角尺和直尺,经过点p,画出与直线a平行的直线吗?试一试,并与同学交流。
a
.P
实验与探究
如图,已知直线a和直线外一点P,能利用三角尺和直尺,经过点P,画出与直线a平行的直线吗?试一试,并与同学交流.
探究新知
一、放
二、贴
三、推
四、画
用两个三角尺也可完成上述操作
探究新知
你能把上面画图的步骤叙述出来吗?
过直线外一点画已知直线的平行线的方法:
①“放”把三角尺的一边放在直线上.
②“贴”用直尺或另一个三角尺紧贴在三角尺
的另一边.
③“推”把第一个三角尺沿直尺边或另一个三
角尺边推到过已知点.
④“画”沿推动后的第一个三角尺边画出直线
探究新知
画一画
1.课本33页 练习 第3题
2.课本34页 习题 第2题
通过上面平行线的画图,你发现经过直线外
一点能作多少条直线与已知直线平行?
平行线的基本性质:
过直线外一点,有且只有一条直线
与这条直线平行.
探究新知
利用平行线的基本性质画图.
已知:直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平
行线平行吗?
如果两条直线都和第三条直线平行,那么这两条直线也相互平行.
平行线基本性质的推论:
简单一点可写成:
平行于同一条直线的两条直线平行.
探究新知
用数学语言表达平行线基本性质的推论:
∵a∥b,a∥c
∴b∥c.
传递性
探究新知
如果直线b//a,c//a,那么直线b//c,即直线b与直线c不相交,你能结合本节课学行线性质解释一下吗?
M
c
b
a
议一议
本节课你学到了哪些知识?
(1)平行线的概念和表示方法;
(2)平行线的画法;
(3)平行线的性质。
小结
1.如图:在
内有一点E,过点E分别画OA、
OB的平行线EC、ED,用符号表示:OA
,
ED
.
A
O
B
D
E
C
//CE
//OB
达标检测
2.判断正误:
(1)在同一平面内,两条不平行的直线是相交线( )
(2)与同一条直线平行的两条直线必平行( )
(3)过直线外一点有且只有一条直线与已知直线平
行( )
√
√
√
3.观察如图所示的正方体并回答.
与AB平行的棱有哪些?
4.如图,过△ABC的顶点分别画对边的平行线,
分别交于D,E,F三点.
习题9.2 : 复习与巩固 1题,2题
作业布置
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
