2.1 认识无理数 课件(共20张PPT)
文档属性
| 名称 | 2.1 认识无理数 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第二章 实数
2.1认识无理数
北师版 数学 八年级上册
学习目标
1.通过拼图活动和勾股定理的应用感受无理数产生的实际背景和引入的必要性。
2.能判断一个数是否为有理数。
情景导入
有理数
整数
分数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
正分数:如 , , 5.2 , …
负分数:如 , ,-3.5 , …
2.除了有理数外还有没有其他的数呢?
1.我们学过的数有哪些?
情景导入
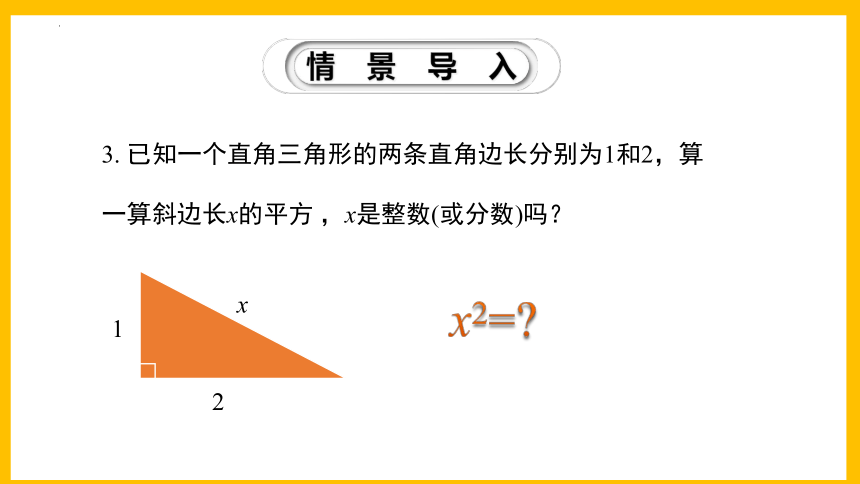
3. 已知一个直角三角形的两条直角边长分别为1和2,算一算斜边长x的平方 ,x是整数(或分数)吗?
x2=
1
2
x
探索新知
无理数的认识
一
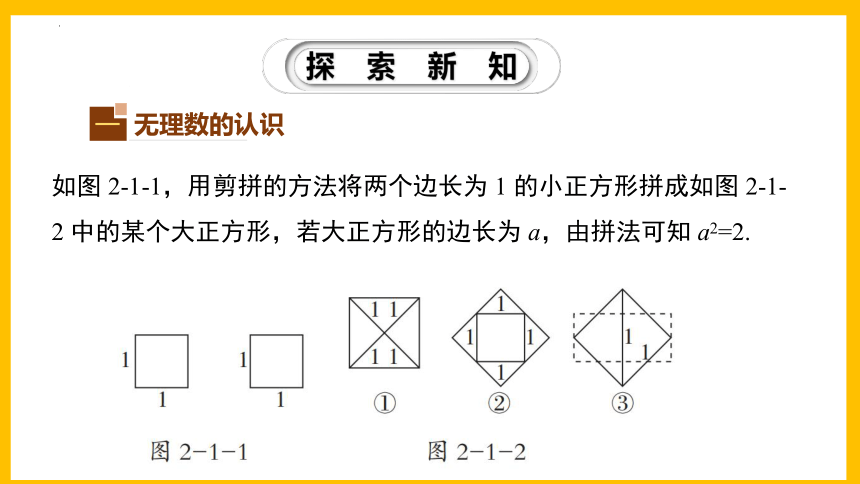
如图 2-1-1,用剪拼的方法将两个边长为 1 的小正方形拼成如图 2-1-2 中的某个大正方形,若大正方形的边长为 a,由拼法可知 a2=2.
探索新知
越来越大,
所以a不可能是整数
a可能是整数吗
探索新知
a可能是以2为分母的分数吗
结果都为分数,所以a不可能是以2为分母的分数。
探索新知
a可能是以3为分母的分数吗
结果都为分数,所以a不可能是以3为分母的分数。
探索新知
a可能是分数吗 试说出原因。
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
a既不是整数又不是分数,所以a一定不是 。
那么a到底是什么数呢?
有理数
古人把这个数取名为无理数。
总结归纳
探索新知
1.无理数的概念 无限不循环小数称为无理数,如圆周率 π =3.141 592 65…,1.010 010 001…(相邻两个 1 之间 0 的个数逐次加 1)等 .
特别提醒
有理数和无理数的区别:
1.无理数是无限不循环小数,有理数是有限小数或无限循环小数;
2.有理数可化为分数,无理数不能化为分数.
探索新知
2. 常见无理数的几种类型
分 类 举 例
一般的无限不循环小数 1.414 213 56…
有规律但不循环的小数 0.101 001 000 1…( 相邻两个 1 之间 0 的个数逐次加 1)
探索新知
某些含 π 的数 2π
开方开不尽的数的方根
(下节会学到) —
无理数与有理数的和或差,结果都是无理数 π +2
无理数乘或除以一个不为 0 的有理数,结果是无理数
当堂检测
1.一个长方形的长与宽分别是3cm,1cm,它的对角线的长是( )
A.整数 B.分数
C.有理数 D.既不是整数,也不是分数
D
2.下列各数: 1, (相邻两个3之间0的个数逐次加1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
A
当堂检测
3.下列结果中,一定是无理数的是( )
A.等腰三角形的高的长度
B.半径为3的圆的周长
C.长方形的对角线的长度
D.体积为有理数的正方体的棱长
B
4.以下各正方形的边长是无理数的是( )
A.面积为25的正方形 B.面积为4/25的正方形
C.面积为8的正方形 D.面积为1.44的正方形
C
当堂检测
5 .满足下列条件的数不是有理数的是( )
C
6.两直角边分别是3和5的直角三角形的斜边长是( )
A. 整数 B. 分数
C. 有理数 D.非有理数
D
C.a2=3
D.2a2=18
B. a2=0.36
A. 2a+5=8
当堂检测
7.下列各数是无理数的是( )
A. 3.14 B. 0 C. -0.101 001 000… D. -4
C
8. 下列说法正确的是 ( )
A. 0.121221222…是有理数
B. 无限小数都是无理数
C. 半径为3的圆周长是有理数
D. 无理数是无限小数
D
当堂检测
9.下列各数:
①面积是2的正方形的边长;
②面积是9的正方形的边长;
③两直角边分别为6和8的直角三角形的斜边长;
④长为4,宽为2的长方形的对角线的长.
其中是无理数的是( )
A.①② B.②③
C.①④ D.③④
C
当堂检测
10.把下列各数填在相应的集合内.
5,π,-|-|,,1.131 331 333 1…(相邻两个1之间依次多一个3),1.6,0.
正分数集合{ …};
非负整数集合{ …};
无理数集合{ …}.
, 1.6
5, 0
π,1.131 331 333 1…(相邻两个1之间依次多一个3)
当堂检测
11.如图,有一个由五个边长为1的小正方形组成的图形,我们可以把它剪拼成一个正方形.则拼成的正方形的面积是多少?这个正方形的边长是有理数吗?
因为小正方形的边长为1,
所以每个小正方形的面积为1,
所以拼成的正方形的面积为 5×1=5.
因为找不到平方等于5的有理数,
所以这个正方形的边长不是有理数.
1.无理数是无限不循环小数,
有理数是有限小数或无限循环小数.
2.任何一个有理数都可以化成分数形式( p≠0, p,q 为整数且互质),而无理数则不能.
第二章 实数
2.1认识无理数
北师版 数学 八年级上册
学习目标
1.通过拼图活动和勾股定理的应用感受无理数产生的实际背景和引入的必要性。
2.能判断一个数是否为有理数。
情景导入
有理数
整数
分数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
正分数:如 , , 5.2 , …
负分数:如 , ,-3.5 , …
2.除了有理数外还有没有其他的数呢?
1.我们学过的数有哪些?
情景导入
3. 已知一个直角三角形的两条直角边长分别为1和2,算一算斜边长x的平方 ,x是整数(或分数)吗?
x2=
1
2
x
探索新知
无理数的认识
一
如图 2-1-1,用剪拼的方法将两个边长为 1 的小正方形拼成如图 2-1-2 中的某个大正方形,若大正方形的边长为 a,由拼法可知 a2=2.
探索新知
越来越大,
所以a不可能是整数
a可能是整数吗
探索新知
a可能是以2为分母的分数吗
结果都为分数,所以a不可能是以2为分母的分数。
探索新知
a可能是以3为分母的分数吗
结果都为分数,所以a不可能是以3为分母的分数。
探索新知
a可能是分数吗 试说出原因。
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
a既不是整数又不是分数,所以a一定不是 。
那么a到底是什么数呢?
有理数
古人把这个数取名为无理数。
总结归纳
探索新知
1.无理数的概念 无限不循环小数称为无理数,如圆周率 π =3.141 592 65…,1.010 010 001…(相邻两个 1 之间 0 的个数逐次加 1)等 .
特别提醒
有理数和无理数的区别:
1.无理数是无限不循环小数,有理数是有限小数或无限循环小数;
2.有理数可化为分数,无理数不能化为分数.
探索新知
2. 常见无理数的几种类型
分 类 举 例
一般的无限不循环小数 1.414 213 56…
有规律但不循环的小数 0.101 001 000 1…( 相邻两个 1 之间 0 的个数逐次加 1)
探索新知
某些含 π 的数 2π
开方开不尽的数的方根
(下节会学到) —
无理数与有理数的和或差,结果都是无理数 π +2
无理数乘或除以一个不为 0 的有理数,结果是无理数
当堂检测
1.一个长方形的长与宽分别是3cm,1cm,它的对角线的长是( )
A.整数 B.分数
C.有理数 D.既不是整数,也不是分数
D
2.下列各数: 1, (相邻两个3之间0的个数逐次加1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
A
当堂检测
3.下列结果中,一定是无理数的是( )
A.等腰三角形的高的长度
B.半径为3的圆的周长
C.长方形的对角线的长度
D.体积为有理数的正方体的棱长
B
4.以下各正方形的边长是无理数的是( )
A.面积为25的正方形 B.面积为4/25的正方形
C.面积为8的正方形 D.面积为1.44的正方形
C
当堂检测
5 .满足下列条件的数不是有理数的是( )
C
6.两直角边分别是3和5的直角三角形的斜边长是( )
A. 整数 B. 分数
C. 有理数 D.非有理数
D
C.a2=3
D.2a2=18
B. a2=0.36
A. 2a+5=8
当堂检测
7.下列各数是无理数的是( )
A. 3.14 B. 0 C. -0.101 001 000… D. -4
C
8. 下列说法正确的是 ( )
A. 0.121221222…是有理数
B. 无限小数都是无理数
C. 半径为3的圆周长是有理数
D. 无理数是无限小数
D
当堂检测
9.下列各数:
①面积是2的正方形的边长;
②面积是9的正方形的边长;
③两直角边分别为6和8的直角三角形的斜边长;
④长为4,宽为2的长方形的对角线的长.
其中是无理数的是( )
A.①② B.②③
C.①④ D.③④
C
当堂检测
10.把下列各数填在相应的集合内.
5,π,-|-|,,1.131 331 333 1…(相邻两个1之间依次多一个3),1.6,0.
正分数集合{ …};
非负整数集合{ …};
无理数集合{ …}.
, 1.6
5, 0
π,1.131 331 333 1…(相邻两个1之间依次多一个3)
当堂检测
11.如图,有一个由五个边长为1的小正方形组成的图形,我们可以把它剪拼成一个正方形.则拼成的正方形的面积是多少?这个正方形的边长是有理数吗?
因为小正方形的边长为1,
所以每个小正方形的面积为1,
所以拼成的正方形的面积为 5×1=5.
因为找不到平方等于5的有理数,
所以这个正方形的边长不是有理数.
1.无理数是无限不循环小数,
有理数是有限小数或无限循环小数.
2.任何一个有理数都可以化成分数形式( p≠0, p,q 为整数且互质),而无理数则不能.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
