5.3.2.1函数的极值 课件(共22张PPT)
文档属性
| 名称 | 5.3.2.1函数的极值 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 21:57:09 | ||
图片预览






文档简介
(共22张PPT)
5.3.2.1函数的极值
新课程标准解读 核心素养
1.了解函数极值的概念,会从几何方面直观地理解函数的极值与导数的关系. 2.掌握函数极值的判定及求法. 3.掌握函数在某一点取得极值的条件. 1.数学抽象:函数极值的概念.
2.数学运算、函数极值的求解.
情境导入
“横看成岭侧成峰,远近高低各不同”,说的是庐山的高低起伏,错落有致.在群山之中,各个山峰的顶端,虽然不一定是群山的最高处,但它却是其附近的最高点,同样,各个谷底虽然不一定是群山之中的最低处,它却是其附近的最低点.
在数学上,这种现象如何来刻画呢?
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的增减。如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
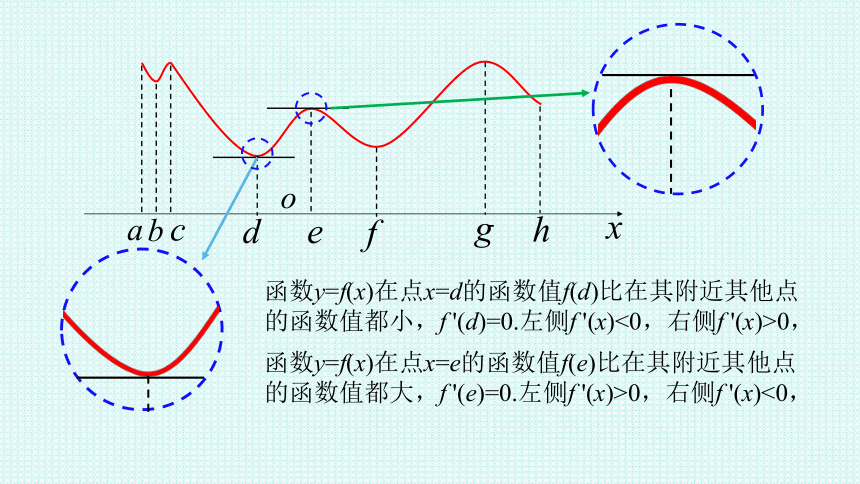
探究1:观察下图,我们发现当t=a时,高台跳水运动员距水面的高度最大,那么函数h(t)在此点处的导数是多少?此点附件的函数图象有什么特点?相应地,导数的正负有什么变化规律
a
b
t
h
O
放大t=a附近的图像,可以看出
h'(t)=0,
当t0;
当t>a时,函数h(t)单调递减,h'(t)<0
对于一般的函数y=f(x),是否具有同样的性质?
函数y=f(x)在点x=d的函数值f(d)比在其附近其他点的函数值都小,f '(d)=0.左侧f '(x)<0,右侧f '(x)>0,
函数y=f(x)在点x=e的函数值f(e)比在其附近其他点的函数值都大,f '(e)=0.左侧f '(x)>0,右侧f '(x)<0,
函数的极值:
一般地,设函数y=f(x)在x0及其附近有定义,如果f(x0)的值比x0附近所有各点的函数值都大,我们说f(x0)是函数y=f(x)的一个极大值;并把x0称为函数f(x)的一个极大值点;
如果f(x0)的值比x0附近所有各点的函数值都小,我们说f(x0)是函数y=f(x)的一个极小值,并把x0称为函数f(x)的一个极小值点.
(1)极值是一个局部概念,极值只是某个点的函数值,与它附近点的函数值比较它是最大值或最小值,但并不意味着它在函数的整个定义域内是最大值或最小值;
(2)一个函数在某区间上或定义域内的极大值或极小值可以不止一个;
(3)函数的极大值与极小值之间无确定的大小关系;
(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点;
(5)单调函数一定没有极值.
探究点1 求函数的极值(点)
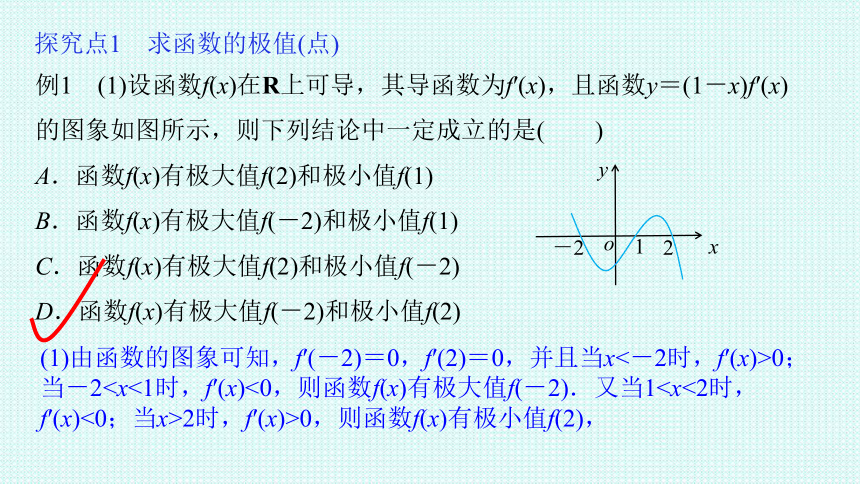
例1 (1)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
o
x
y
1
2
(1)由函数的图象可知,f′(-2)=0,f′(2)=0,并且当x<-2时,f′(x)>0;当-22时,f′(x)>0,则函数f(x)有极小值f(2),
-2
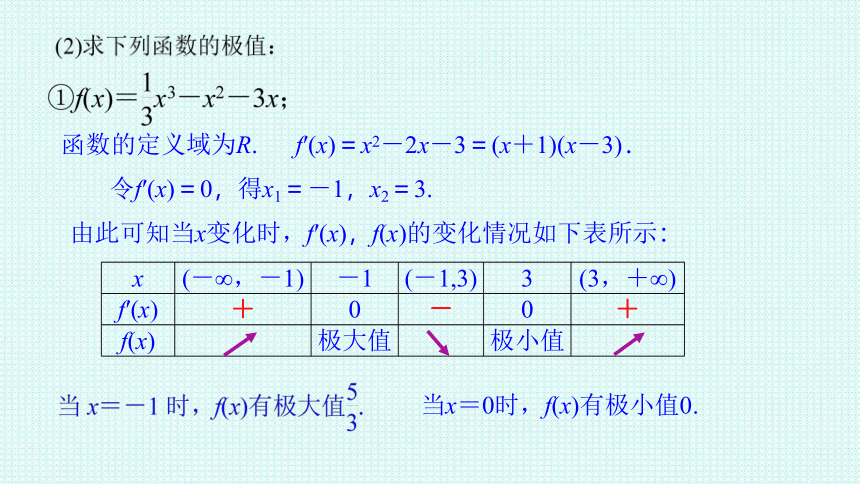
函数的定义域为R. f′(x)=x2-2x-3=(x+1)(x-3).
令f′(x)=0,得x1=-1,x2=3.
由此可知当x变化时,f′(x),f(x)的变化情况如下表所示:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f′(x) + 0 - 0 +
f(x) 极大值 极小值
当x=0时,f(x)有极小值0.
当x变化时,f′(x)与f(x)的变化情况如下表:
x (0,e) e (e,+∞)
f′(x) + 0 -
f(x) 极大值
故当x=e时函数取得极大值,
函数的定义域为R.
令f′(x)=0,得x(2-x)·e-x=0,解得x=0或x=2.
x (-∞,0) 0 (0,2) 2 (2,+∞)
f′(x) - 0 + 0 -
f(x) 极小值 极大值
当x=0时,f(x)有极小值,并且极小值为f(0)=0;
当x=2时,f(x)有极大值,并且极大值为f(2)=
函数极值和极值点的求解步骤
(1)确定函数的定义域;
(2)求方程f′(x)=0的根;
(3)用方程f′(x)=0的根顺次将函数的定义域分成若干个小开区间,并列成表格;
(4)由f′(x)在方程f′(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况.
探究点2 含参数的函数极值问题
角度一 含参数的函数极值求法
例2若函数f(x)=x-aln x(a∈R),求函数f(x)的极值.
函数f(x)的定义域为(0,+∞),
(1)当a≤0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增,函数f(x)无极值.
(2)当a>0时,令f′(x)=0,解得x=a.
当0a时,f′(x)>0.
∴f(x)在x=a处取得极小值,且f(a)=a-aln a,无极大值.
综上可知,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
求解析式中含有参数的函数极值时,有时需要用分类讨论的思想才能解决问题.讨论的依据有两种:一是看参数是否对f′(x)的零点有影响,若有影响,则需要分类讨论;二是看f′(x)在其零点附近的符号的确定是否与参数有关,若有关,则需要分类讨论.
求函数f(x)=x3-3ax+b(a≠0)的极值.
解:f′(x)=3(x2-a)(a≠0),
当a<0时,f′(x)>0恒成立,即函数在(-∞,+∞)上单调递增,此时函数没有极值;
当a>0时,令f′(x)=0,
当x变化时,f′(x)与f(x)的变化情况如下表:
x (-∞,- ) - (- , ) ( ,+∞)
f′(x) + 0 - 0 +
f(x) 单调递增 极大值f(- ) 单调递减 极小值f( ) 单调递增
角度二 已知函数的极值求参数值或范围
例3(1)已知函数f(x)=x3+ax2+bx+a2在x=1处取极值10,则a=( )
A.4或-3 B.4或-11
C.4 D.-3
(1)∵f(x)=x3+ax2+bx+a2,∴f′(x)=3x2+2ax+b.
f′(x)=3x2-6x+3=3(x-1)2≥0,
故函数f(x)单调递增,无极值,不符合题意
令f′(x)<0,得0令f′(x)>0,得x>1.f(x)在x=1处取极小值.
必有一个正数解x=-a,
①若a=-1,此正数解为x=1,此时
f(x)在(0,+∞)上单调递增,无极值.
②若a≠-1,此正数解为x≠1,f′(x)=0必有2个不同的正数解,f(x)存在2个极值.综上,a=-1,
1.已知函数的极值求参数
(1)待定系数法:常根据极值点处导数为0和极值两条件列出方程组,用待定系数法求解;
(2)验证:因为导数值为0不一定此点就是极值点,故利用上述方程组解出的解必须验证.
2.对于函数无极值的问题,往往转化为f′(x)≥0或f′(x)≤0在某区间内恒成立的问题,此时需注意不等式中的等号是否成立.
由题意知f′(1)=2+a=0.解得a=-2,故f(x)=2ln x-2x,x>0,
令f′(x)<0,得x>1,故f′(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以x=1是极大值点,符合题意
2.设a∈R,若函数y=ex+ax有大于零的极值点,则实数a的取值范围是________.
∵y=ex+ax,∴y′=ex+a,由题意知方程ex+a=0有大于零的解.
∵当x>0时,-ex<-1,∴a=-ex<-1.
探究点3 利用导数研究方程根(函数零点)的问题
例4已知函数f(x)=x3-3x+a(a为实数),若方程f(x)=0有三个不同实根,求实数a的取值范围.
令f′(x)=3x2-3=3(x+1)(x-1)=0,解得x1=-1,x2=1.
当x<-1时,f′(x)>0;当-1当x>1时,f′(x)>0.所以当x=-1时,f(x)有极大值f(-1)=2+a;
当x=1时,f(x)有极小值f(1)=-2+a.
因为方程f(x)=0有三个不同实根,所以y=f(x)的图象与x轴有三个交点,如图.
o
x
y
1
-1
解得-2利用导数研究方程根(函数零点)的问题的步骤
(1)利用导数判断函数的单调性;
(2)研究函数的极值情况;
(3)在上述研究的基础上画出函数的大致图象;
(4)直观上判断函数的图象与x轴的交点或两个图象的交点的个数.若含有参数,则需要讨论极值的正负.
给定三次函数f(x)=ax3+bx2+cx+d(a≠0),求导得f′(x)=3ax2+2bx+c.用Δ表示方程f′(x)=0的根的判别式,有以下结论:
(1)当Δ=4(b2-3ac)>0时,有两个极值点;
当Δ=4(b2-3ac)≤0时,无极值点.
(2)函数f(x)的图象存在水平切线,则f′(x)=0有实数解,从而Δ=4(b2-3ac)≥0;
(3)函数在R上单调递增,则a>0且Δ=4(b2-3ac)≤0.
已知函数f(x)=x3-3x+m只有一个零点,则实数m的取值范围是 ( )
A.[-2,2] B.(-∞,-2)∪(2,+∞)
C.(-2,2) D.(-∞,-2]∪[2,+∞)
f′(x)=3x2-3.
由f′(x)>0,得x>1或x<-1,此时函数单调递增;
由f′(x)<0,得-1<x<1,此时函数单调递减.
即当x=-1时,函数f(x)取得极大值;当x=1时,函数f(x)取得极小值.
要使函数f(x)=x3-3x+m只有一个零点,则需满足f(-1)·f(1)>0,
即(m+2)(m-2)>0,解得m>2或m<-2.
综上,实数m的取值范围是m<-2或m>2.
5.3.2.1函数的极值
新课程标准解读 核心素养
1.了解函数极值的概念,会从几何方面直观地理解函数的极值与导数的关系. 2.掌握函数极值的判定及求法. 3.掌握函数在某一点取得极值的条件. 1.数学抽象:函数极值的概念.
2.数学运算、函数极值的求解.
情境导入
“横看成岭侧成峰,远近高低各不同”,说的是庐山的高低起伏,错落有致.在群山之中,各个山峰的顶端,虽然不一定是群山的最高处,但它却是其附近的最高点,同样,各个谷底虽然不一定是群山之中的最低处,它却是其附近的最低点.
在数学上,这种现象如何来刻画呢?
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的增减。如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
探究1:观察下图,我们发现当t=a时,高台跳水运动员距水面的高度最大,那么函数h(t)在此点处的导数是多少?此点附件的函数图象有什么特点?相应地,导数的正负有什么变化规律
a
b
t
h
O
放大t=a附近的图像,可以看出
h'(t)=0,
当t
当t>a时,函数h(t)单调递减,h'(t)<0
对于一般的函数y=f(x),是否具有同样的性质?
函数y=f(x)在点x=d的函数值f(d)比在其附近其他点的函数值都小,f '(d)=0.左侧f '(x)<0,右侧f '(x)>0,
函数y=f(x)在点x=e的函数值f(e)比在其附近其他点的函数值都大,f '(e)=0.左侧f '(x)>0,右侧f '(x)<0,
函数的极值:
一般地,设函数y=f(x)在x0及其附近有定义,如果f(x0)的值比x0附近所有各点的函数值都大,我们说f(x0)是函数y=f(x)的一个极大值;并把x0称为函数f(x)的一个极大值点;
如果f(x0)的值比x0附近所有各点的函数值都小,我们说f(x0)是函数y=f(x)的一个极小值,并把x0称为函数f(x)的一个极小值点.
(1)极值是一个局部概念,极值只是某个点的函数值,与它附近点的函数值比较它是最大值或最小值,但并不意味着它在函数的整个定义域内是最大值或最小值;
(2)一个函数在某区间上或定义域内的极大值或极小值可以不止一个;
(3)函数的极大值与极小值之间无确定的大小关系;
(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点;
(5)单调函数一定没有极值.
探究点1 求函数的极值(点)
例1 (1)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
o
x
y
1
2
(1)由函数的图象可知,f′(-2)=0,f′(2)=0,并且当x<-2时,f′(x)>0;当-2
-2
函数的定义域为R. f′(x)=x2-2x-3=(x+1)(x-3).
令f′(x)=0,得x1=-1,x2=3.
由此可知当x变化时,f′(x),f(x)的变化情况如下表所示:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f′(x) + 0 - 0 +
f(x) 极大值 极小值
当x=0时,f(x)有极小值0.
当x变化时,f′(x)与f(x)的变化情况如下表:
x (0,e) e (e,+∞)
f′(x) + 0 -
f(x) 极大值
故当x=e时函数取得极大值,
函数的定义域为R.
令f′(x)=0,得x(2-x)·e-x=0,解得x=0或x=2.
x (-∞,0) 0 (0,2) 2 (2,+∞)
f′(x) - 0 + 0 -
f(x) 极小值 极大值
当x=0时,f(x)有极小值,并且极小值为f(0)=0;
当x=2时,f(x)有极大值,并且极大值为f(2)=
函数极值和极值点的求解步骤
(1)确定函数的定义域;
(2)求方程f′(x)=0的根;
(3)用方程f′(x)=0的根顺次将函数的定义域分成若干个小开区间,并列成表格;
(4)由f′(x)在方程f′(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况.
探究点2 含参数的函数极值问题
角度一 含参数的函数极值求法
例2若函数f(x)=x-aln x(a∈R),求函数f(x)的极值.
函数f(x)的定义域为(0,+∞),
(1)当a≤0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增,函数f(x)无极值.
(2)当a>0时,令f′(x)=0,解得x=a.
当0
∴f(x)在x=a处取得极小值,且f(a)=a-aln a,无极大值.
综上可知,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
求解析式中含有参数的函数极值时,有时需要用分类讨论的思想才能解决问题.讨论的依据有两种:一是看参数是否对f′(x)的零点有影响,若有影响,则需要分类讨论;二是看f′(x)在其零点附近的符号的确定是否与参数有关,若有关,则需要分类讨论.
求函数f(x)=x3-3ax+b(a≠0)的极值.
解:f′(x)=3(x2-a)(a≠0),
当a<0时,f′(x)>0恒成立,即函数在(-∞,+∞)上单调递增,此时函数没有极值;
当a>0时,令f′(x)=0,
当x变化时,f′(x)与f(x)的变化情况如下表:
x (-∞,- ) - (- , ) ( ,+∞)
f′(x) + 0 - 0 +
f(x) 单调递增 极大值f(- ) 单调递减 极小值f( ) 单调递增
角度二 已知函数的极值求参数值或范围
例3(1)已知函数f(x)=x3+ax2+bx+a2在x=1处取极值10,则a=( )
A.4或-3 B.4或-11
C.4 D.-3
(1)∵f(x)=x3+ax2+bx+a2,∴f′(x)=3x2+2ax+b.
f′(x)=3x2-6x+3=3(x-1)2≥0,
故函数f(x)单调递增,无极值,不符合题意
令f′(x)<0,得0
必有一个正数解x=-a,
①若a=-1,此正数解为x=1,此时
f(x)在(0,+∞)上单调递增,无极值.
②若a≠-1,此正数解为x≠1,f′(x)=0必有2个不同的正数解,f(x)存在2个极值.综上,a=-1,
1.已知函数的极值求参数
(1)待定系数法:常根据极值点处导数为0和极值两条件列出方程组,用待定系数法求解;
(2)验证:因为导数值为0不一定此点就是极值点,故利用上述方程组解出的解必须验证.
2.对于函数无极值的问题,往往转化为f′(x)≥0或f′(x)≤0在某区间内恒成立的问题,此时需注意不等式中的等号是否成立.
由题意知f′(1)=2+a=0.解得a=-2,故f(x)=2ln x-2x,x>0,
令f′(x)<0,得x>1,故f′(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以x=1是极大值点,符合题意
2.设a∈R,若函数y=ex+ax有大于零的极值点,则实数a的取值范围是________.
∵y=ex+ax,∴y′=ex+a,由题意知方程ex+a=0有大于零的解.
∵当x>0时,-ex<-1,∴a=-ex<-1.
探究点3 利用导数研究方程根(函数零点)的问题
例4已知函数f(x)=x3-3x+a(a为实数),若方程f(x)=0有三个不同实根,求实数a的取值范围.
令f′(x)=3x2-3=3(x+1)(x-1)=0,解得x1=-1,x2=1.
当x<-1时,f′(x)>0;当-1
当x=1时,f(x)有极小值f(1)=-2+a.
因为方程f(x)=0有三个不同实根,所以y=f(x)的图象与x轴有三个交点,如图.
o
x
y
1
-1
解得-2
(1)利用导数判断函数的单调性;
(2)研究函数的极值情况;
(3)在上述研究的基础上画出函数的大致图象;
(4)直观上判断函数的图象与x轴的交点或两个图象的交点的个数.若含有参数,则需要讨论极值的正负.
给定三次函数f(x)=ax3+bx2+cx+d(a≠0),求导得f′(x)=3ax2+2bx+c.用Δ表示方程f′(x)=0的根的判别式,有以下结论:
(1)当Δ=4(b2-3ac)>0时,有两个极值点;
当Δ=4(b2-3ac)≤0时,无极值点.
(2)函数f(x)的图象存在水平切线,则f′(x)=0有实数解,从而Δ=4(b2-3ac)≥0;
(3)函数在R上单调递增,则a>0且Δ=4(b2-3ac)≤0.
已知函数f(x)=x3-3x+m只有一个零点,则实数m的取值范围是 ( )
A.[-2,2] B.(-∞,-2)∪(2,+∞)
C.(-2,2) D.(-∞,-2]∪[2,+∞)
f′(x)=3x2-3.
由f′(x)>0,得x>1或x<-1,此时函数单调递增;
由f′(x)<0,得-1<x<1,此时函数单调递减.
即当x=-1时,函数f(x)取得极大值;当x=1时,函数f(x)取得极小值.
要使函数f(x)=x3-3x+m只有一个零点,则需满足f(-1)·f(1)>0,
即(m+2)(m-2)>0,解得m>2或m<-2.
综上,实数m的取值范围是m<-2或m>2.
