5.3.2.3导数的综合应用 课件(共20张PPT)
文档属性
| 名称 | 5.3.2.3导数的综合应用 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 21:58:38 | ||
图片预览








文档简介
(共20张PPT)
5.3.2.3导数的综合应用
新课程标准解读 核心素养
1.体会导数与单调性、极值、最大(小)值的关系. 2.感悟利用导数解决与不等式、函数零点有关的问题. 1.逻辑推理:利用导数求解和函数相关问题.
2.数学运算:导数的计算.
探究点1 导数与不等式
角度一 利用导数比较大小、解不等式
f′(x)=1-sin x≥0,所以y=f(x)在x∈R上单调递增,
又由0.3-1>2-0.3>log20.2,可得f(0.3-1)>f(2-0.3)>f(log2 0.2),
(2)(2021·安徽省皖江名校联盟联考)函数y=f(x),x∈R,f(1)=2 021,对任意的x∈R,都有f′(x)-3x2>0成立,则不等式f(x)A.(-∞,-1) B.(-1,1)
C.(1,+∞) D.(-∞,1)
设h(x)=f(x)-x3,则h′(x)=f′(x)-3x2>0,所以h(x)在R上单调递增,
h(1)=f(1)-13=2 020,
而f(x)即h(x)所以x<1
角度二 证明不等式
因为x>1,所以f′(x)>0,
在(1,+∞)上单调递增,
所以f(x)>f(1)=ln 1+1=1.
对于任意x∈R,ex≥x+1.(当且仅当x=0时等号成立)
设f(x)=ex-x+1,f'(x)=ex-1
x∈(-∞,0)时,f'(x)<0,f(x)单调递减,x∈(0,+∞)时,f(x)单调递增,[f(x)]min=f(0)=0
f(x)≥f(0),即ex-x+1≥0,ex≥x+1.
角度三 不等式恒成立问题
(2021·安徽省皖江名校联盟高三联考)若函数f(x)=-x2+4x+b ln x在(0,+∞)上单调递减,则b的取值范围是( )
A.(-∞,-2] B.(-∞,-2)
C.(-2,+∞) D.[-2,+∞)
f(x)=-x2+4x+b ln x在(0,+∞)上单调递减,即f′(x)≤0在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
即b≤(2x2-4x)min,
因为2x2-4x=2(x-1)2-2≥-2,
所以b≤-2,
探究点2 导数与函数的零点
角度一 判断函数零点个数
m∈R,讨论函数g(x)
零点的个数.
则φ′(x)=-x2+1=-(x-1)(x+1),
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减.
所以x=1是φ(x)的唯一极值点且是极大值点.
因此x=1也是φ(x)的最大值点.
又φ(0)=0,结合y=φ(x)的图象(如图),
o
x
y
y=φ(x)
1
函数g(x)有且只有一个零点;
函数g(x)有两个零点;
④当m≤0时,函数g(x)有且只有一个零点.
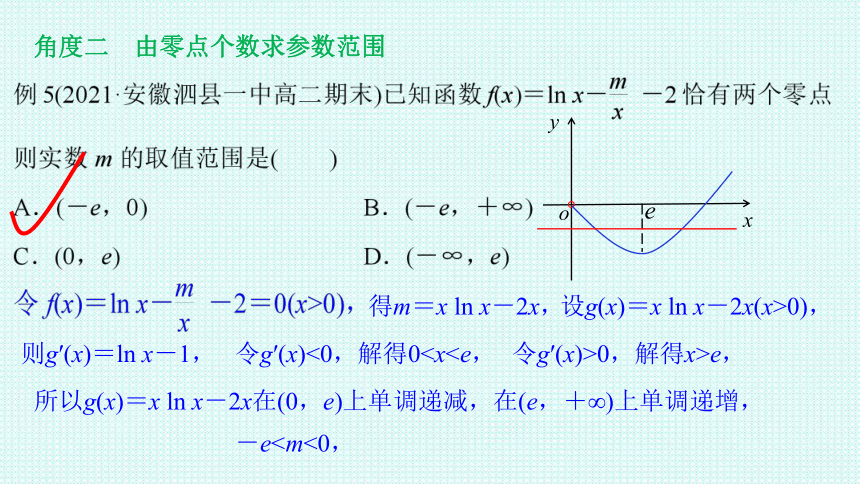
角度二 由零点个数求参数范围
得m=x ln x-2x,
设g(x)=x ln x-2x(x>0),
则g′(x)=ln x-1,
令g′(x)<0,解得0令g′(x)>0,解得x>e,
所以g(x)=x ln x-2x在(0,e)上单调递减,在(e,+∞)上单调递增,
o
x
y
e
-e若函数f(x)=ex-ax2,a∈R在(0,+∞)上有两个不同的零点,求实数a的取值范围.
则函数f(x)在(0,+∞)上有两个不同的零点,
数k(x)的图象在(0,+∞)上有两个不同的交点,
( )
令k′(x)=0得x=2,
k′(x)<0,所以k(x)在(0,2)上单调递增,在(2,+∞)上单调递减,
当x∈(0,2)时,k′(x)>0,当x∈(2,+∞)时,
所以k(x)在(0,+∞)上的最大值为
有两个不同的交点,
方法归纳
已知函数零点个数求参数的常用方法
(1)分离参数法:首先分离出参数,然后利用求导的方法求出构造的新函数的最值,根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围.
(2)分类讨论法:结合单调性,先确定参数分类的标准,在每个小范围内研究零点的个数是否符合题意,将满足题意的参数的各小范围并在一起,即为所求参数范围.
跟踪训练 若函数g(x)=ex(x-2)-m有两个零点,求实数m的取值范围.
g(x)=ex(x-2)-m,函数g(x)=ex(x-2)-m有两个零点,
相当于曲线u(x)=ex·(x-2)与直线y=m有两个交点.
u′(x)=ex·(x-2)+ex=ex(x-1),当x∈(-∞,1)时,u′(x)<0,
所以u(x)在(-∞,1)上单调递减,当x∈(1,+∞)时,u′(x)>0
所以u(x)在(1,+∞)上单调递增,
所以x=1时,u(x)取得极小值u(1)=-e,又x→+∞时,u(x)→+∞;x<2时,u(x)<0,所以-e探究点3 导数在实际问题中的应用
类型一 几何中的最值问题
例6 请你设计一个包装盒,如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,
B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒.点E,F在边AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=x(cm).某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
令V′(x)=0,得x=0(舍去)或x=20.
∵当00;当20∴V(x)在x=20时取极大值也是唯一的极值,故为最大值.
将一块2 m×6 m的矩形钢板按如图所示的方式划线,要求①至⑦全为矩形,沿线裁去阴影部分,把剩余部分焊接成一个以⑦为底,⑤⑥为盖的水箱,设水箱的高为x m,容积为y m3.
(1)写出y关于x的函数关系式;
(2)当x取何值时,水箱的容积最大?
①
③
④
⑤
⑥
②
⑦
(1)由水箱的高为x m,得水箱底面的宽为(2-2x)m,
故水箱的容积y=(2-2x)(3-x)x=2x3-8x2+6x(0(2)由(1)得y′=6x2-16x+6,令y′=0,
所以y=2x3-8x2+6x(0类型二 生活中的最值问题
命题角度1 利润最大问题
因为当x=5时,y=11,
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
由(1)可知,该商品每日的销售量为
所以商场每日销售该商品所获得的利润为
f(x)=(x-3)
=2+10(x-3)(x-6)2,3从而f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)(x-6),令f′(x)=0,得x=4或x=6.当x变化时,f′(x),f(x)的变化情况如下表:
x (3,4) 4 (4,6)
f′(x) + 0 -
f(x) ↗ 极大值 ↘
所以当x=4时,函数f(x)取得最大值,且最大值等于42.
命题角度2 用料、费用最少问题
例8 某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+ )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元. (1)试写出y关于x的函数关系式;
设需新建n个桥墩,
(2)当m=640米时,需新建多少个桥墩才能使y最小?
1
2
x
1
2
-
令f′(x)=0,得 =512,所以x=64.
x
3
2
x
3
2
当0当640,f(x)在区间(64,640)上为增函数,
所以f(x)在x=64处取得最小值.
(1)用料最省、成本最低问题是日常生活中常见的问题之一,解决这类问题要明确自变量的意义以及最值问题所研究的对象.正确书写函数表达式,准确求导,结合实际作答.
(2)利用导数的方法解决实际问题,当在定义区间内只有一个点使f′(x)=0时,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知道在这个点取得最大(小)值.
5.3.2.3导数的综合应用
新课程标准解读 核心素养
1.体会导数与单调性、极值、最大(小)值的关系. 2.感悟利用导数解决与不等式、函数零点有关的问题. 1.逻辑推理:利用导数求解和函数相关问题.
2.数学运算:导数的计算.
探究点1 导数与不等式
角度一 利用导数比较大小、解不等式
f′(x)=1-sin x≥0,所以y=f(x)在x∈R上单调递增,
又由0.3-1>2-0.3>log20.2,可得f(0.3-1)>f(2-0.3)>f(log2 0.2),
(2)(2021·安徽省皖江名校联盟联考)函数y=f(x),x∈R,f(1)=2 021,对任意的x∈R,都有f′(x)-3x2>0成立,则不等式f(x)
C.(1,+∞) D.(-∞,1)
设h(x)=f(x)-x3,则h′(x)=f′(x)-3x2>0,所以h(x)在R上单调递增,
h(1)=f(1)-13=2 020,
而f(x)
角度二 证明不等式
因为x>1,所以f′(x)>0,
在(1,+∞)上单调递增,
所以f(x)>f(1)=ln 1+1=1.
对于任意x∈R,ex≥x+1.(当且仅当x=0时等号成立)
设f(x)=ex-x+1,f'(x)=ex-1
x∈(-∞,0)时,f'(x)<0,f(x)单调递减,x∈(0,+∞)时,f(x)单调递增,[f(x)]min=f(0)=0
f(x)≥f(0),即ex-x+1≥0,ex≥x+1.
角度三 不等式恒成立问题
(2021·安徽省皖江名校联盟高三联考)若函数f(x)=-x2+4x+b ln x在(0,+∞)上单调递减,则b的取值范围是( )
A.(-∞,-2] B.(-∞,-2)
C.(-2,+∞) D.[-2,+∞)
f(x)=-x2+4x+b ln x在(0,+∞)上单调递减,即f′(x)≤0在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
即b≤(2x2-4x)min,
因为2x2-4x=2(x-1)2-2≥-2,
所以b≤-2,
探究点2 导数与函数的零点
角度一 判断函数零点个数
m∈R,讨论函数g(x)
零点的个数.
则φ′(x)=-x2+1=-(x-1)(x+1),
当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减.
所以x=1是φ(x)的唯一极值点且是极大值点.
因此x=1也是φ(x)的最大值点.
又φ(0)=0,结合y=φ(x)的图象(如图),
o
x
y
y=φ(x)
1
函数g(x)有且只有一个零点;
函数g(x)有两个零点;
④当m≤0时,函数g(x)有且只有一个零点.
角度二 由零点个数求参数范围
得m=x ln x-2x,
设g(x)=x ln x-2x(x>0),
则g′(x)=ln x-1,
令g′(x)<0,解得0
所以g(x)=x ln x-2x在(0,e)上单调递减,在(e,+∞)上单调递增,
o
x
y
e
-e
则函数f(x)在(0,+∞)上有两个不同的零点,
数k(x)的图象在(0,+∞)上有两个不同的交点,
( )
令k′(x)=0得x=2,
k′(x)<0,所以k(x)在(0,2)上单调递增,在(2,+∞)上单调递减,
当x∈(0,2)时,k′(x)>0,当x∈(2,+∞)时,
所以k(x)在(0,+∞)上的最大值为
有两个不同的交点,
方法归纳
已知函数零点个数求参数的常用方法
(1)分离参数法:首先分离出参数,然后利用求导的方法求出构造的新函数的最值,根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围.
(2)分类讨论法:结合单调性,先确定参数分类的标准,在每个小范围内研究零点的个数是否符合题意,将满足题意的参数的各小范围并在一起,即为所求参数范围.
跟踪训练 若函数g(x)=ex(x-2)-m有两个零点,求实数m的取值范围.
g(x)=ex(x-2)-m,函数g(x)=ex(x-2)-m有两个零点,
相当于曲线u(x)=ex·(x-2)与直线y=m有两个交点.
u′(x)=ex·(x-2)+ex=ex(x-1),当x∈(-∞,1)时,u′(x)<0,
所以u(x)在(-∞,1)上单调递减,当x∈(1,+∞)时,u′(x)>0
所以u(x)在(1,+∞)上单调递增,
所以x=1时,u(x)取得极小值u(1)=-e,又x→+∞时,u(x)→+∞;x<2时,u(x)<0,所以-e
类型一 几何中的最值问题
例6 请你设计一个包装盒,如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,
B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒.点E,F在边AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=x(cm).某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
令V′(x)=0,得x=0(舍去)或x=20.
∵当0
将一块2 m×6 m的矩形钢板按如图所示的方式划线,要求①至⑦全为矩形,沿线裁去阴影部分,把剩余部分焊接成一个以⑦为底,⑤⑥为盖的水箱,设水箱的高为x m,容积为y m3.
(1)写出y关于x的函数关系式;
(2)当x取何值时,水箱的容积最大?
①
③
④
⑤
⑥
②
⑦
(1)由水箱的高为x m,得水箱底面的宽为(2-2x)m,
故水箱的容积y=(2-2x)(3-x)x=2x3-8x2+6x(0
所以y=2x3-8x2+6x(0
命题角度1 利润最大问题
因为当x=5时,y=11,
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
由(1)可知,该商品每日的销售量为
所以商场每日销售该商品所获得的利润为
f(x)=(x-3)
=2+10(x-3)(x-6)2,3
x (3,4) 4 (4,6)
f′(x) + 0 -
f(x) ↗ 极大值 ↘
所以当x=4时,函数f(x)取得最大值,且最大值等于42.
命题角度2 用料、费用最少问题
例8 某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+ )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元. (1)试写出y关于x的函数关系式;
设需新建n个桥墩,
(2)当m=640米时,需新建多少个桥墩才能使y最小?
1
2
x
1
2
-
令f′(x)=0,得 =512,所以x=64.
x
3
2
x
3
2
当0
所以f(x)在x=64处取得最小值.
(1)用料最省、成本最低问题是日常生活中常见的问题之一,解决这类问题要明确自变量的意义以及最值问题所研究的对象.正确书写函数表达式,准确求导,结合实际作答.
(2)利用导数的方法解决实际问题,当在定义区间内只有一个点使f′(x)=0时,如果函数在这点有极大(小)值,那么不与端点值比较,也可以知道在这个点取得最大(小)值.
