5.3.2.2函数的最大(小)值 课件(共20张PPT)
文档属性
| 名称 | 5.3.2.2函数的最大(小)值 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 22:00:09 | ||
图片预览








文档简介
(共20张PPT)
5.3.2.2函数的最大(小)值
新课程标准解读 核心素养
1.理解函数最值的概念. 2.会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次) 1.数学抽象:函数最值概念.
2.数学运算:求函数最值.
o
x
y
2
3
-2
-3
-3
2
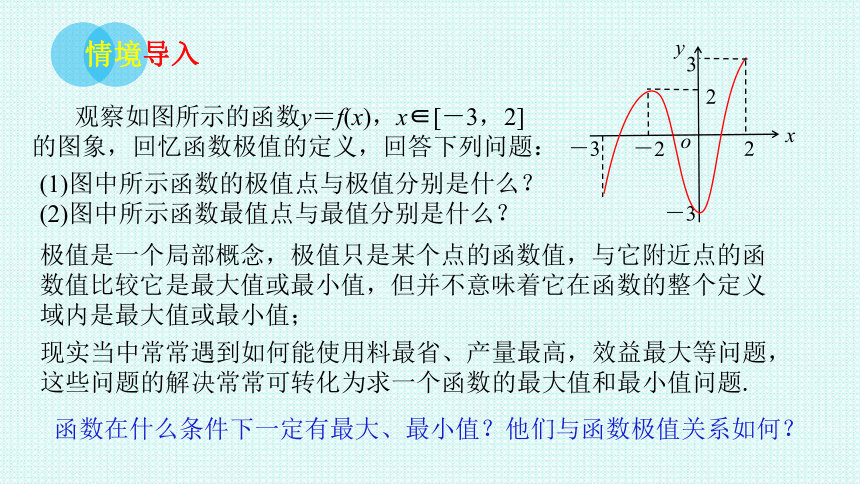
观察如图所示的函数y=f(x),x∈[-3,2]的图象,回忆函数极值的定义,回答下列问题:
情境导入
(1)图中所示函数的极值点与极值分别是什么?(2)图中所示函数最值点与最值分别是什么?
极值是一个局部概念,极值只是某个点的函数值,与它附近点的函数值比较它是最大值或最小值,但并不意味着它在函数的整个定义域内是最大值或最小值;
现实当中常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题.
函数在什么条件下一定有最大、最小值?他们与函数极值关系如何?
一、函数最值的定义
1.一般地,如果在区间[a,b]上函数y=f(x)的图象是一条____________的曲线,那么它必有最大值和最小值.
连续不断
2.对于函数f(x),给定区间I,若对任意x∈I,存在x0∈I,使得f(x)________ f(x0),则称f(x0)为函数f(x)在区间I上的最小值;若对任意x∈I,存在x0∈I,使得f(x)________ f(x0),则称f(x0)为函数f(x)在区间I上的最大值.
≥
≤
二、求函数的最大值与最小值的步骤
函数y=f(x)在区间[a,b]上连续,在区间(a,b)内可导,求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)求函数y=f(x)在区间(a,b)上的________;
(2)将函数y=f(x)的各极值与端点处的函数值________,________比较,其中最大的一个是最大值,最小的一个是最小值.
极值
f(a)
f(b)
函数极值与最值的关系
(1)函数的极值是函数在某一点附近的局部概念,函数的最大值和最小值是一个整体性概念;
(2)函数的最大值、最小值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,函数的极值可以有多个,但最值只能有一个;
(3)极值只能在区间内取得,最值则可以在端点处取得.有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值不在端点处取得时必定是极值.
探究点1 求函数的最值
例1(链接教科书第93页例6)当x∈[-1,1]时,
因为-1≤x≤1,所以2-x>0,当-1≤x<0时,
函数单调递减,
函数单调递增,
故当x=-1时,函数取得最大值e.
令f′(x)=0可得x=e,
则当00,f(x)单调递增,
当e当x=e时,f(x)取极大值也为最大值,
所以f(x)max=f(e)=eln e -e=0.
因为f′(x)=6x2-12x=6x(x-2),由f′(x)=0得x=0或2.
又f(0)=m,f(2)=-8+m,f(-2)=-40+m,显然f(0)>f(2)>f(-2),
所以m=3,最小值为f(-2)=-37.
x [-2,0) 0 (0,2) 2
f′(x) + 0 - 0
f(x) 极大值
例2已知函数f(x)=x3-ax2-a2x,求函数f(x)在[0,+∞)上的最小值.
解:f′(x)=3x2-2ax-a2=(3x+a)(x-a),
①当a>0时,令f′(x)<0,解得0≤x0,解得x>a.所以f(x)在[0,a)上单调递减,在[a,+∞)上单调递增.所以f(x)min=f(a)=-a3.
②当a=0时,f′(x)=3x2≥0,f(x)在[0,+∞)上递增.所以f(x)min=f(0)=0.
③当a<0时,令f′(x)<0,
例3已知函数f(x)=ln x-ax(a∈R).
(1)求函数f(x)的单调区间;(2)当a>0时,求函数f(x)在[1,2]上的最小值.
即函数f(x)的单调增区间为(0,+∞).
即a≥1时,函数f(x)在区间[1,2]上是减函数,
所以f(x)的最小值是f(2)=ln 2-2a.
函数f(x)在区间[1,2]上是增函数,
所以f(x)的最小值是f(1)=-a.
上是增函数,
又f(2)-f(1)=ln 2-a.
最小值是f(1)=-a.
当ln 2≤a<1时,最小值为f(2)=ln 2-2a.
综上可知,当0当a≥ln 2时,函数f(x)的最小值是ln 2-2a.
含参数的函数最值问题
(1)能根据条件确定出参数,从而化为不含参数函数的最值问题;
(2)对于不能求出参数值的问题,则要对参数进行讨论,其实质是讨论导函数大于0,等于0,小于0三种情况.若导函数恒不等于0,则函数在已知区间上是单调函数,最值在端点处取得;若导函数可能等于0,则求出极值点后求极值,再与端点值比较后确定最值.
探究点2 不等式恒成立问题
例4设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).
(1)求f(x)的最小值h(t);
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
解(1)∵f(x)=t(x+t)2-t3+t-1(x∈R,t>0),∴当x=-t时,f(x)取最小值,即f(-t)=-t3+t-1,即h(t)=-t3+t-1.
(2)令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g′(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g′(t),g(t)的变化情况如下表:
t (0,1) 1 (1,2)
g′(t) + 0 -
g(t) 单调递增 极大值1-m 单调递减
∴g(t)在(0,2)内有极大值也为最大值g(1)=1-m.
h(t)<-2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,即等价于1-m<0.∴m的取值范围为(1,+∞).
(变条件)若将本例(2)的条件改为“存在t∈[0,2],使h(t)<-2t+m成立”,如何求解?
令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g′(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).
当t变化时,g′(t),g(t)的变化情况如下表:
t 0 (0,1) 1 (1,2) 2
g′(t) + 0 -
g(t) -1-m 单调递增 极大值1-m 单调递减 -3-m
∴g(t)在[0,2]上有最小值g(2)=-3-m,存在t∈[0,2],使h(t)<-2t+m成立,等价于g(t)的最小值g(2)<0.
∴-3-m<0,∴m>-3,
∴实数m的取值范围为(-3,+∞).
解析:构造函数g(x)=exf(x)-ex-1,
则g′(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1].
由已知f(x)+f′(x)>1,可得g′(x)>0,所以g(x)为R上的增函数.
又因为g(0)=e0f(0)-e0-1=0,所以当x>0时,g(x)>g(0)=0,
即exf(x)>ex+1.
故不等式exf(x)>ex+1的解集为{x|x>0}.
(1)求a,b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)f′(x)=3x2+2ax+b,
因为f′(1)=3+2a+b=0,
所以f′(x)=3x2-x-2=(3x+2)(x-1),
当x变化时,f′(x),f(x)的变化情况如下表:
x 1 (1,+∞)
f′(x) + 0 - 0 +
f(x) ↗ 极大值 ↘ 极小值 ↗
因为f(2)=2+c,所以f(2)=2+c为最大值.
要使f(x)f(2)=2+c,
解得c<-1或c>2.
故实数c的取值范围为(-∞,-1)∪(2,+∞).
已知函数f(x)=2xln x,g(x)=-x2+ax-3对一切x∈(0,+∞),f(x)≥g(x)恒成立,则a的取值范围是__________.
由2xln x≥-x2+ax-3,
当x∈(0,1)时,h′(x)<0,h(x)单调递减,当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.∴h(x)min=h(1)=4.∴a≤4.
5.3.2.2函数的最大(小)值
新课程标准解读 核心素养
1.理解函数最值的概念. 2.会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次) 1.数学抽象:函数最值概念.
2.数学运算:求函数最值.
o
x
y
2
3
-2
-3
-3
2
观察如图所示的函数y=f(x),x∈[-3,2]的图象,回忆函数极值的定义,回答下列问题:
情境导入
(1)图中所示函数的极值点与极值分别是什么?(2)图中所示函数最值点与最值分别是什么?
极值是一个局部概念,极值只是某个点的函数值,与它附近点的函数值比较它是最大值或最小值,但并不意味着它在函数的整个定义域内是最大值或最小值;
现实当中常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题.
函数在什么条件下一定有最大、最小值?他们与函数极值关系如何?
一、函数最值的定义
1.一般地,如果在区间[a,b]上函数y=f(x)的图象是一条____________的曲线,那么它必有最大值和最小值.
连续不断
2.对于函数f(x),给定区间I,若对任意x∈I,存在x0∈I,使得f(x)________ f(x0),则称f(x0)为函数f(x)在区间I上的最小值;若对任意x∈I,存在x0∈I,使得f(x)________ f(x0),则称f(x0)为函数f(x)在区间I上的最大值.
≥
≤
二、求函数的最大值与最小值的步骤
函数y=f(x)在区间[a,b]上连续,在区间(a,b)内可导,求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)求函数y=f(x)在区间(a,b)上的________;
(2)将函数y=f(x)的各极值与端点处的函数值________,________比较,其中最大的一个是最大值,最小的一个是最小值.
极值
f(a)
f(b)
函数极值与最值的关系
(1)函数的极值是函数在某一点附近的局部概念,函数的最大值和最小值是一个整体性概念;
(2)函数的最大值、最小值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,函数的极值可以有多个,但最值只能有一个;
(3)极值只能在区间内取得,最值则可以在端点处取得.有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值不在端点处取得时必定是极值.
探究点1 求函数的最值
例1(链接教科书第93页例6)当x∈[-1,1]时,
因为-1≤x≤1,所以2-x>0,当-1≤x<0时,
函数单调递减,
函数单调递增,
故当x=-1时,函数取得最大值e.
令f′(x)=0可得x=e,
则当0
当e
所以f(x)max=f(e)=eln e -e=0.
因为f′(x)=6x2-12x=6x(x-2),由f′(x)=0得x=0或2.
又f(0)=m,f(2)=-8+m,f(-2)=-40+m,显然f(0)>f(2)>f(-2),
所以m=3,最小值为f(-2)=-37.
x [-2,0) 0 (0,2) 2
f′(x) + 0 - 0
f(x) 极大值
例2已知函数f(x)=x3-ax2-a2x,求函数f(x)在[0,+∞)上的最小值.
解:f′(x)=3x2-2ax-a2=(3x+a)(x-a),
①当a>0时,令f′(x)<0,解得0≤x
②当a=0时,f′(x)=3x2≥0,f(x)在[0,+∞)上递增.所以f(x)min=f(0)=0.
③当a<0时,令f′(x)<0,
例3已知函数f(x)=ln x-ax(a∈R).
(1)求函数f(x)的单调区间;(2)当a>0时,求函数f(x)在[1,2]上的最小值.
即函数f(x)的单调增区间为(0,+∞).
即a≥1时,函数f(x)在区间[1,2]上是减函数,
所以f(x)的最小值是f(2)=ln 2-2a.
函数f(x)在区间[1,2]上是增函数,
所以f(x)的最小值是f(1)=-a.
上是增函数,
又f(2)-f(1)=ln 2-a.
最小值是f(1)=-a.
当ln 2≤a<1时,最小值为f(2)=ln 2-2a.
综上可知,当0
含参数的函数最值问题
(1)能根据条件确定出参数,从而化为不含参数函数的最值问题;
(2)对于不能求出参数值的问题,则要对参数进行讨论,其实质是讨论导函数大于0,等于0,小于0三种情况.若导函数恒不等于0,则函数在已知区间上是单调函数,最值在端点处取得;若导函数可能等于0,则求出极值点后求极值,再与端点值比较后确定最值.
探究点2 不等式恒成立问题
例4设函数f(x)=tx2+2t2x+t-1(x∈R,t>0).
(1)求f(x)的最小值h(t);
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
解(1)∵f(x)=t(x+t)2-t3+t-1(x∈R,t>0),∴当x=-t时,f(x)取最小值,即f(-t)=-t3+t-1,即h(t)=-t3+t-1.
(2)令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g′(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).当t变化时,g′(t),g(t)的变化情况如下表:
t (0,1) 1 (1,2)
g′(t) + 0 -
g(t) 单调递增 极大值1-m 单调递减
∴g(t)在(0,2)内有极大值也为最大值g(1)=1-m.
h(t)<-2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,即等价于1-m<0.∴m的取值范围为(1,+∞).
(变条件)若将本例(2)的条件改为“存在t∈[0,2],使h(t)<-2t+m成立”,如何求解?
令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g′(t)=-3t2+3=0,得t=1或t=-1(不合题意,舍去).
当t变化时,g′(t),g(t)的变化情况如下表:
t 0 (0,1) 1 (1,2) 2
g′(t) + 0 -
g(t) -1-m 单调递增 极大值1-m 单调递减 -3-m
∴g(t)在[0,2]上有最小值g(2)=-3-m,存在t∈[0,2],使h(t)<-2t+m成立,等价于g(t)的最小值g(2)<0.
∴-3-m<0,∴m>-3,
∴实数m的取值范围为(-3,+∞).
解析:构造函数g(x)=exf(x)-ex-1,
则g′(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1].
由已知f(x)+f′(x)>1,可得g′(x)>0,所以g(x)为R上的增函数.
又因为g(0)=e0f(0)-e0-1=0,所以当x>0时,g(x)>g(0)=0,
即exf(x)>ex+1.
故不等式exf(x)>ex+1的解集为{x|x>0}.
(1)求a,b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)
因为f′(1)=3+2a+b=0,
所以f′(x)=3x2-x-2=(3x+2)(x-1),
当x变化时,f′(x),f(x)的变化情况如下表:
x 1 (1,+∞)
f′(x) + 0 - 0 +
f(x) ↗ 极大值 ↘ 极小值 ↗
因为f(2)=2+c,所以f(2)=2+c为最大值.
要使f(x)
解得c<-1或c>2.
故实数c的取值范围为(-∞,-1)∪(2,+∞).
已知函数f(x)=2xln x,g(x)=-x2+ax-3对一切x∈(0,+∞),f(x)≥g(x)恒成立,则a的取值范围是__________.
由2xln x≥-x2+ax-3,
当x∈(0,1)时,h′(x)<0,h(x)单调递减,当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.∴h(x)min=h(1)=4.∴a≤4.
