2022-2023学年初中数学苏科版(新版)七年级上册2.4.1相反数 教学课件 (共19张PPT)
文档属性
| 名称 | 2022-2023学年初中数学苏科版(新版)七年级上册2.4.1相反数 教学课件 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 729.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
(1) 如果规定向东为正,那么,某人向东走5米记作____,又向西走5米记作_____.
(2)如果规定零上的温度为正,那么,白天的温度为零上3.5度,记作______,某天夜间的温度为零下3.5度,记作_____.
(3)如果规定收入为正,那么,某学生利用暑假期间打工收入400元,记作_____,开学后交学费400元,记作_______.
+5m
-5m
+3.5度
-3.5度
-400元
+400元
§2.4 相反数
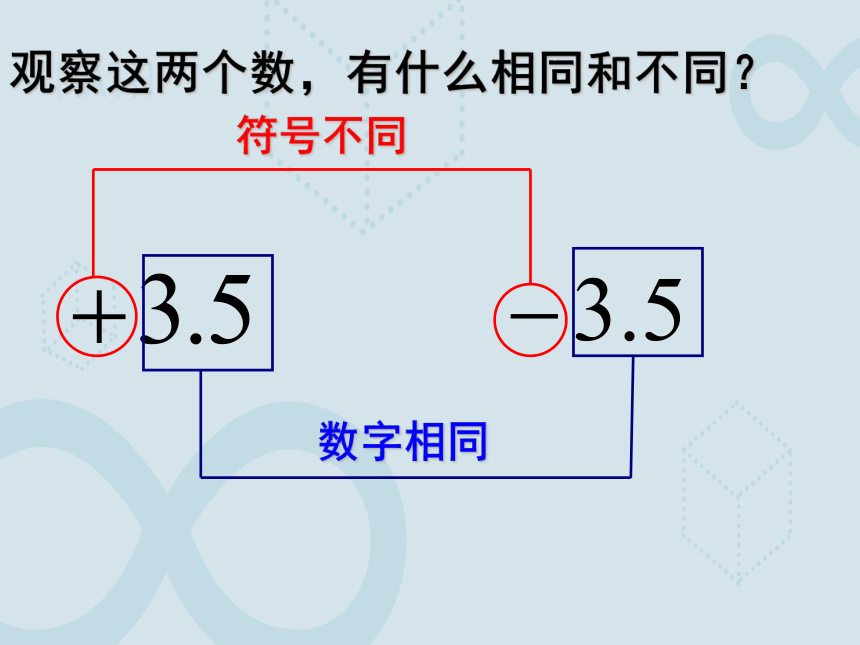
观察这两个数,有什么相同和不同?
数字相同
符号不同
请同学们在数轴上画出下列各组数的点,并观察每一组数中的两个数有什么相同点和不同点 在数轴上表示每一组数的两个点有怎样的位置关系?
(1) 1.5 和 -1.5
(2) 5 和 -5
- 5 -4 -3 -2 -1
0
1 2 3 4 5
1.5
-1.5
5
-5
只有符号不同的两个数叫做互为相反数。
例如: 1.5和-1.5互为相反数.
即 1.5是-1.5的相反数;
-1.5是1.5的相反数.
数轴上表示相反数的两个点和原点有什么关系?
答:在数轴上表示互为相反数的两个数的点,
分别位于原点的两旁,且与原点的距离相等。
想一想1
想一想2
0的相反数是 (从数轴上考虑)
答: 0的相反数是0。
例1.分别写出下列各数的相反数:
5,-7,- ,+11.2
解: 5的相反数是-5
-7的相反数是7
+11.2的相反数是-11.2
的相反数是
1. 填空:
(1) 2.5的相反数是_____;
(2) _____是 -100的相反数;
(3) 是_____的相反数;
(4) ______的相反数是-1.1;
(5) 8.2和_____互为相反数.
练习:
-2.5
100
1.1
-8.2
2. 判断:
(1) +3是-3的相反数
(2) -3是3的相反数
(3) -3和+3都是相反数
(4) -3与+3互为相反数
(5) 一个数的相反数不可能是它本身
(6) -2是- (-2)的相反数
√
√
×
√
×
√
我们通常把在一个数前面添上“-”号,表示这个数的相反数.
例如: - (-4)=4
- (+5.5)=-5.5
-0=0
同样,在一个数前面添上“+”号,
表示这个数本身.
例如: +(-4)=-4
+(+12)=12
+0=0
例2 化简下列各数:
(1) -(+10) (2) +(-0.15)
(3) +(+3) (4) -(-20)
解: (1) -(+10)=-10
(2) +(-0.15)=-0.15
(3) +(+3)=+3 = 3
(4) -(-20)=20
1.化简:
(1) - (+0.78) (2) +(+ )
(3) -(-3.14) (4) +(-10.1)
2.判断下列语句是否正确,为什么 (1)符号相反的两个数叫做互为相反数; (2)相反数和我们以前学过的倒数是一样的; (3)一个数的相反数的相反数等于原来的数;
(4)互为相反数的两个数不一定一个是正数,
一个是负数
练习:
你发现了括号内外的符号“联手”对结果符号的影响吗?试说说你的发现(可讨论)
-5
-4.3
5.2
1
-1
结论:
1.简化符号时:同号得正,异号得负
2.出现多重符号时看“-”的个数,
当“-”是奇数个时,结果为负,
当“-”是偶数个时,结果为正。
1
-[-(+1)]=
+[+(-1)]=
-{-[-(-1)]}=
-[-(-1)]=
-1
想一想3
+(-5)=
-(- )=
-(+4.3)=
+(+5.2)=
化简下列各数中的符号:
(1)
(2) -(+5)
(3) -[-(-7)]
(4) -{+[-(+3)]}
练习:
=-5
=-7
=3
例3.(1)如果数轴上的两点A , B所表示的数互为相反数,点A在原点的左侧,并且A,B之间的距离是8 ,那么点B所表示的数是_____.
(2) 若a=-72时,则-a =_____.
若-x=-63时,则 x=_____.
(3) 若a + 4 =0 , 则 a =______.
4
72
63
-4
(1) 8的相反数是________;
(2) -(-7)是_____的相反数;
(3) -(+4)是_______的相反数;
(4) m的相反数是0.1,m是________;
(5) 相反数是它本身的数是________;
(6) 任何有理数都有相反数,对吗?
(7) 若a=-13, 则-a=_______,
若-a=-6,则a=_________.
练习:
-8
4
-0.1
0
对
13
6
-7
应用创新
如图:是一个正方形纸盒的展开图,若在其中的三个正方形A,B,C内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A,B,C内的三个数依次为_____ 、______、 _____.
A
B
-1
2
C
0
1
-2
0
课堂小结
本节课学习了以下内容:
1.相反数的概念:只有符号不同的两个数,我们说其中一个是另一个的相反数.
2.利用相反数的知识来化简.
3.正数的相反数是_______,
负数的相反数是_______,
0的相反数是_______.
负数
正数
0
4.回答下列问题:
(1) 什么数的相反数大于本身?
(2) 什么数的相反数等于本身?
(3) 什么数的相反数小于本身?
负数
0
正数
思考题
1.如果-a=-9, 那么-a的相反数是_____.
2. a的相反数是_______.
a-4的相反数是__________.
3-x的相反数是__________.
3.已知a、b互为相反数,b、c互为相反数,
且c=5.2,则c-a+b=______.
4.已知有理数a大于1,有理数b大于-1且小于0,试将有理数a、b、-a、-b按从小到大的顺序排列.
9
-a
-(a-4)
-(3-x)
-5.2
(1) 如果规定向东为正,那么,某人向东走5米记作____,又向西走5米记作_____.
(2)如果规定零上的温度为正,那么,白天的温度为零上3.5度,记作______,某天夜间的温度为零下3.5度,记作_____.
(3)如果规定收入为正,那么,某学生利用暑假期间打工收入400元,记作_____,开学后交学费400元,记作_______.
+5m
-5m
+3.5度
-3.5度
-400元
+400元
§2.4 相反数
观察这两个数,有什么相同和不同?
数字相同
符号不同
请同学们在数轴上画出下列各组数的点,并观察每一组数中的两个数有什么相同点和不同点 在数轴上表示每一组数的两个点有怎样的位置关系?
(1) 1.5 和 -1.5
(2) 5 和 -5
- 5 -4 -3 -2 -1
0
1 2 3 4 5
1.5
-1.5
5
-5
只有符号不同的两个数叫做互为相反数。
例如: 1.5和-1.5互为相反数.
即 1.5是-1.5的相反数;
-1.5是1.5的相反数.
数轴上表示相反数的两个点和原点有什么关系?
答:在数轴上表示互为相反数的两个数的点,
分别位于原点的两旁,且与原点的距离相等。
想一想1
想一想2
0的相反数是 (从数轴上考虑)
答: 0的相反数是0。
例1.分别写出下列各数的相反数:
5,-7,- ,+11.2
解: 5的相反数是-5
-7的相反数是7
+11.2的相反数是-11.2
的相反数是
1. 填空:
(1) 2.5的相反数是_____;
(2) _____是 -100的相反数;
(3) 是_____的相反数;
(4) ______的相反数是-1.1;
(5) 8.2和_____互为相反数.
练习:
-2.5
100
1.1
-8.2
2. 判断:
(1) +3是-3的相反数
(2) -3是3的相反数
(3) -3和+3都是相反数
(4) -3与+3互为相反数
(5) 一个数的相反数不可能是它本身
(6) -2是- (-2)的相反数
√
√
×
√
×
√
我们通常把在一个数前面添上“-”号,表示这个数的相反数.
例如: - (-4)=4
- (+5.5)=-5.5
-0=0
同样,在一个数前面添上“+”号,
表示这个数本身.
例如: +(-4)=-4
+(+12)=12
+0=0
例2 化简下列各数:
(1) -(+10) (2) +(-0.15)
(3) +(+3) (4) -(-20)
解: (1) -(+10)=-10
(2) +(-0.15)=-0.15
(3) +(+3)=+3 = 3
(4) -(-20)=20
1.化简:
(1) - (+0.78) (2) +(+ )
(3) -(-3.14) (4) +(-10.1)
2.判断下列语句是否正确,为什么 (1)符号相反的两个数叫做互为相反数; (2)相反数和我们以前学过的倒数是一样的; (3)一个数的相反数的相反数等于原来的数;
(4)互为相反数的两个数不一定一个是正数,
一个是负数
练习:
你发现了括号内外的符号“联手”对结果符号的影响吗?试说说你的发现(可讨论)
-5
-4.3
5.2
1
-1
结论:
1.简化符号时:同号得正,异号得负
2.出现多重符号时看“-”的个数,
当“-”是奇数个时,结果为负,
当“-”是偶数个时,结果为正。
1
-[-(+1)]=
+[+(-1)]=
-{-[-(-1)]}=
-[-(-1)]=
-1
想一想3
+(-5)=
-(- )=
-(+4.3)=
+(+5.2)=
化简下列各数中的符号:
(1)
(2) -(+5)
(3) -[-(-7)]
(4) -{+[-(+3)]}
练习:
=-5
=-7
=3
例3.(1)如果数轴上的两点A , B所表示的数互为相反数,点A在原点的左侧,并且A,B之间的距离是8 ,那么点B所表示的数是_____.
(2) 若a=-72时,则-a =_____.
若-x=-63时,则 x=_____.
(3) 若a + 4 =0 , 则 a =______.
4
72
63
-4
(1) 8的相反数是________;
(2) -(-7)是_____的相反数;
(3) -(+4)是_______的相反数;
(4) m的相反数是0.1,m是________;
(5) 相反数是它本身的数是________;
(6) 任何有理数都有相反数,对吗?
(7) 若a=-13, 则-a=_______,
若-a=-6,则a=_________.
练习:
-8
4
-0.1
0
对
13
6
-7
应用创新
如图:是一个正方形纸盒的展开图,若在其中的三个正方形A,B,C内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A,B,C内的三个数依次为_____ 、______、 _____.
A
B
-1
2
C
0
1
-2
0
课堂小结
本节课学习了以下内容:
1.相反数的概念:只有符号不同的两个数,我们说其中一个是另一个的相反数.
2.利用相反数的知识来化简.
3.正数的相反数是_______,
负数的相反数是_______,
0的相反数是_______.
负数
正数
0
4.回答下列问题:
(1) 什么数的相反数大于本身?
(2) 什么数的相反数等于本身?
(3) 什么数的相反数小于本身?
负数
0
正数
思考题
1.如果-a=-9, 那么-a的相反数是_____.
2. a的相反数是_______.
a-4的相反数是__________.
3-x的相反数是__________.
3.已知a、b互为相反数,b、c互为相反数,
且c=5.2,则c-a+b=______.
4.已知有理数a大于1,有理数b大于-1且小于0,试将有理数a、b、-a、-b按从小到大的顺序排列.
9
-a
-(a-4)
-(3-x)
-5.2
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
