2022-2023学年初中数学苏科版(新版)七年级上册2.4.2绝对值 教学课件 (共13张PPT)
文档属性
| 名称 | 2022-2023学年初中数学苏科版(新版)七年级上册2.4.2绝对值 教学课件 (共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
巩固复习:
1.填空:(1) -2的相反数是_________.
(2) -(-3.75)与_________互为相反数.
(3) 相反数是其本身的数是______.
2.下列说法正确的是 ( )
A. -(+5)的相反数是-5;
B.符号不同的两个数互为相反数;
C.p 的相反数是 ―3.14;
D.任何一个有理数都有相反数;
3.一个数的相反数是非正数, 那么这个数一定是( )
A. 正数 B. 负数
C. 零或正数 D. 零
2
-3.75
0
D
C
§2.4 绝对值
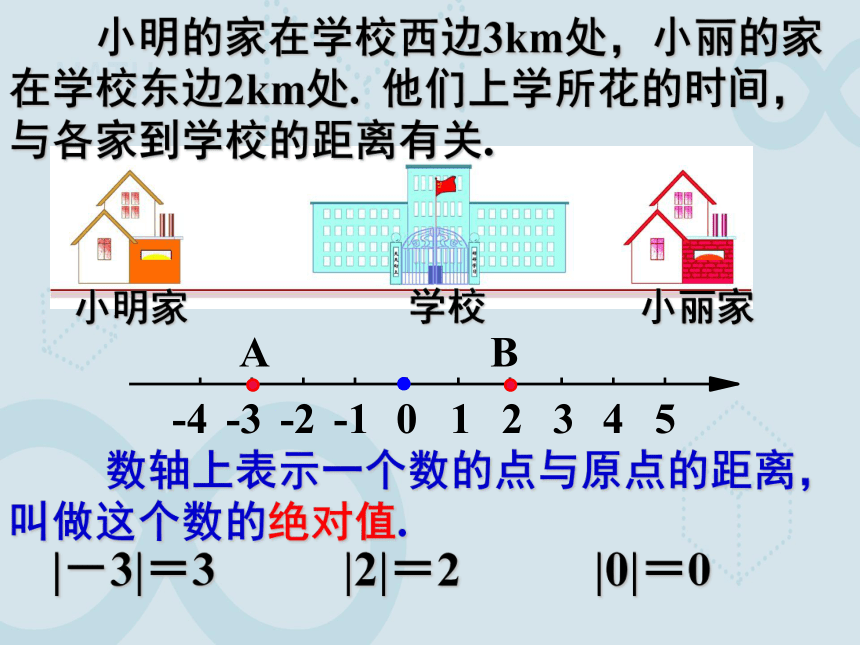
小明家
小丽家
小明的家在学校西边3km处,小丽的家在学校东边2km处. 他们上学所花的时间,与各家到学校的距离有关.
B
A
-4
-3
-2
-1
5
4
3
2
1
0
数轴上表示一个数的点与原点的距离,
叫做这个数的绝对值.
学校
|-3|=3
|2|=2
|0|=0
|-(-4.75)|=4.75
|+(-2.5)|=2.5
=
例1 .求下列各数的绝对值
-(-4.75),+(-2.5),0
, +10,
解:
|+10|=10
|0|=0
2. 填空:
(1)绝对值是5.1,符号是“-”号的数是_____.
-5.1
(2)绝对值等于0的数是_____.
(3) _______绝对值等于2.
(4)如果|a|=3,并且a<0,则a=_______.
-3
0
±2
练习:
1. 求下列各数的绝对值与相反数:
-5,4.5,-(+0.5),+(-1),0
3.回答下列问题:
(1) 绝对值是12的数有几个 是什么
答: 绝对值是12的数有2个,它们是12和-12
(2) 绝对值是0的数有几个 是什么
答: 绝对值是0的数有1个,是0
(3) 有没有绝对值是-3的数 为什么
答: 没有绝对值是-3的数,因为任何有理数
的绝对值总是正数或0(通常也称非负数).
例2.比较-3与-6的绝对值的大小.
解:
因为 |-3|=3,|-6|=6
并且 3<6
所以 |-3|<|-6|
练习:
求-3、-0.4、-2的绝对值,并用“<”号把这些绝对值连接起来。
例3.绝对值小于3的整数有哪几个
练习:
(1)绝对值不大于3的整数有哪几个
(2)绝对值小于10的整数一共有多少个
(3)绝对值不大于2的非负整数有哪几个
分析:
-4
-3
-2
-1
5
4
3
2
1
0
解:绝对值小于3的整数有
-2、-1、0、1、2,共5个.
一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3
一个负数的绝对值是它的相反数
0的绝对值是0
例如:|0|=0
1.绝对值等于本身的有哪些数
答: 绝对值等于本身的有正数或0
2.绝对值等于它的相反数的有哪些数
答:绝对值等于它的相反数的有负数或0
因为正数可用a>0表示,负数可用a<0表示
(1)当a是正数时,|a|=_____;
(2)当a是负数时,|a|=_____;
(3)当a=0时,|a|=_____.
a
-a
0
由此可以看出,不论有理数a取何值,
它的绝对值总是正数或0(通常也称非负数).
即对任意有理数a,总有
|a|≥0
正数的绝对值是它本身
0的绝对值是0
负数的绝对值是它的相反数
互为相反数的两个数的绝对值相等
课堂小结
本节我们主要学习了绝对值的意义:
一个数的绝对值的意义是数轴上表示这个数的点与原点的距离;
知道任何数的绝对值一定是非负数。
2、绝对值为3的数是 .
1、3的绝对值是____;-3的绝对值是____.
3、|-4|=_____;|+(-2.5)|=______.
5、绝对值最小的数是_________.
6、绝对值小于4.5的整数
是___________________.
4、绝对值等于本身的数是_________.
7、绝对值不大于3的负整数是___________.
3
3
±3
4
2.5
正数或0
0
0,±1, ±2, ±3 ,±4
-1,-2,-3
8、(1)当a >b时,|a-b|=_____;
(2)当a <b时,|a-b|=_____;
巩固复习:
1.填空:(1) -2的相反数是_________.
(2) -(-3.75)与_________互为相反数.
(3) 相反数是其本身的数是______.
2.下列说法正确的是 ( )
A. -(+5)的相反数是-5;
B.符号不同的两个数互为相反数;
C.p 的相反数是 ―3.14;
D.任何一个有理数都有相反数;
3.一个数的相反数是非正数, 那么这个数一定是( )
A. 正数 B. 负数
C. 零或正数 D. 零
2
-3.75
0
D
C
§2.4 绝对值
小明家
小丽家
小明的家在学校西边3km处,小丽的家在学校东边2km处. 他们上学所花的时间,与各家到学校的距离有关.
B
A
-4
-3
-2
-1
5
4
3
2
1
0
数轴上表示一个数的点与原点的距离,
叫做这个数的绝对值.
学校
|-3|=3
|2|=2
|0|=0
|-(-4.75)|=4.75
|+(-2.5)|=2.5
=
例1 .求下列各数的绝对值
-(-4.75),+(-2.5),0
, +10,
解:
|+10|=10
|0|=0
2. 填空:
(1)绝对值是5.1,符号是“-”号的数是_____.
-5.1
(2)绝对值等于0的数是_____.
(3) _______绝对值等于2.
(4)如果|a|=3,并且a<0,则a=_______.
-3
0
±2
练习:
1. 求下列各数的绝对值与相反数:
-5,4.5,-(+0.5),+(-1),0
3.回答下列问题:
(1) 绝对值是12的数有几个 是什么
答: 绝对值是12的数有2个,它们是12和-12
(2) 绝对值是0的数有几个 是什么
答: 绝对值是0的数有1个,是0
(3) 有没有绝对值是-3的数 为什么
答: 没有绝对值是-3的数,因为任何有理数
的绝对值总是正数或0(通常也称非负数).
例2.比较-3与-6的绝对值的大小.
解:
因为 |-3|=3,|-6|=6
并且 3<6
所以 |-3|<|-6|
练习:
求-3、-0.4、-2的绝对值,并用“<”号把这些绝对值连接起来。
例3.绝对值小于3的整数有哪几个
练习:
(1)绝对值不大于3的整数有哪几个
(2)绝对值小于10的整数一共有多少个
(3)绝对值不大于2的非负整数有哪几个
分析:
-4
-3
-2
-1
5
4
3
2
1
0
解:绝对值小于3的整数有
-2、-1、0、1、2,共5个.
一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3
一个负数的绝对值是它的相反数
0的绝对值是0
例如:|0|=0
1.绝对值等于本身的有哪些数
答: 绝对值等于本身的有正数或0
2.绝对值等于它的相反数的有哪些数
答:绝对值等于它的相反数的有负数或0
因为正数可用a>0表示,负数可用a<0表示
(1)当a是正数时,|a|=_____;
(2)当a是负数时,|a|=_____;
(3)当a=0时,|a|=_____.
a
-a
0
由此可以看出,不论有理数a取何值,
它的绝对值总是正数或0(通常也称非负数).
即对任意有理数a,总有
|a|≥0
正数的绝对值是它本身
0的绝对值是0
负数的绝对值是它的相反数
互为相反数的两个数的绝对值相等
课堂小结
本节我们主要学习了绝对值的意义:
一个数的绝对值的意义是数轴上表示这个数的点与原点的距离;
知道任何数的绝对值一定是非负数。
2、绝对值为3的数是 .
1、3的绝对值是____;-3的绝对值是____.
3、|-4|=_____;|+(-2.5)|=______.
5、绝对值最小的数是_________.
6、绝对值小于4.5的整数
是___________________.
4、绝对值等于本身的数是_________.
7、绝对值不大于3的负整数是___________.
3
3
±3
4
2.5
正数或0
0
0,±1, ±2, ±3 ,±4
-1,-2,-3
8、(1)当a >b时,|a-b|=_____;
(2)当a <b时,|a-b|=_____;
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
