人教版数学九年级上册22.1.4二次函数y=ax2+bx+c的图象和性质同步练习 (含答案)
文档属性
| 名称 | 人教版数学九年级上册22.1.4二次函数y=ax2+bx+c的图象和性质同步练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 359.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 16:33:45 | ||
图片预览


文档简介
22.1.4 二次函数y=ax +bx+c的图象和性质
班级: 姓名: 成绩:
一、选择题
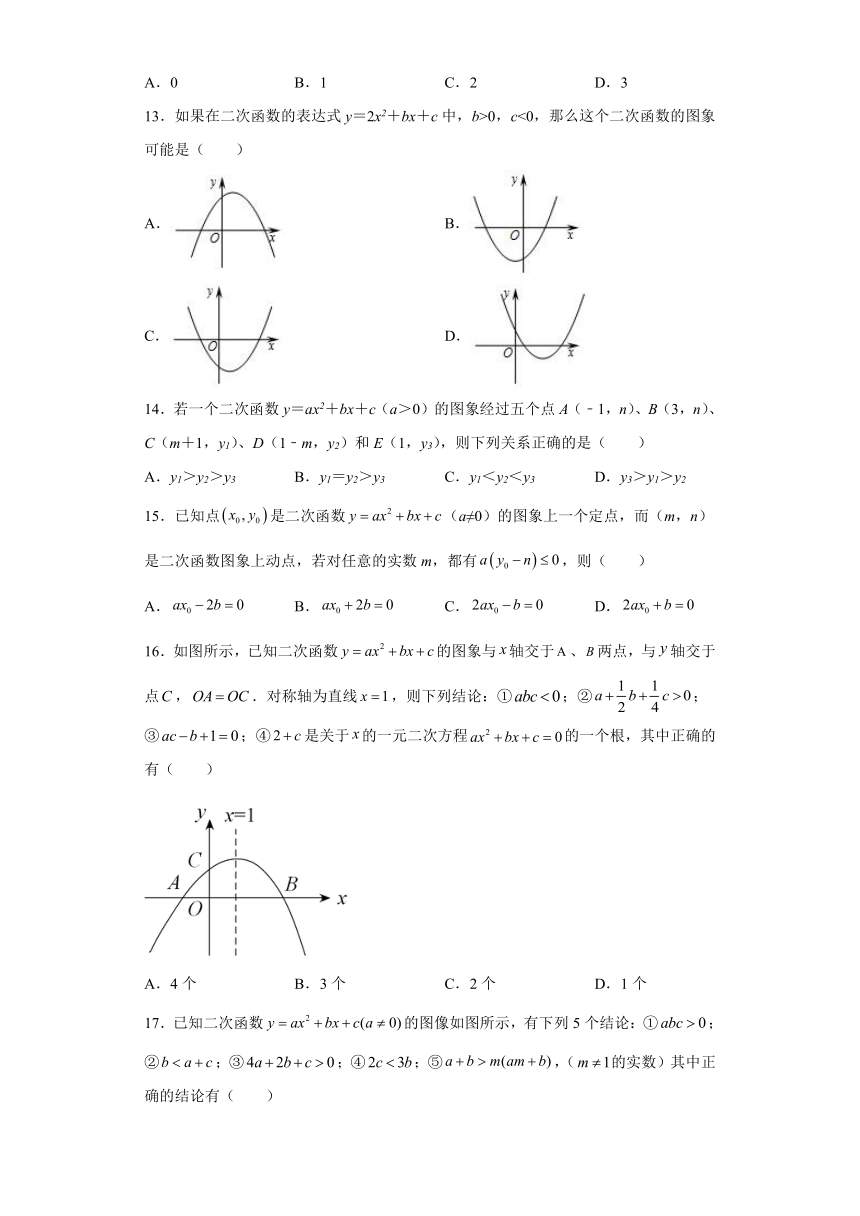
1.若两个图形重叠后.重叠部分的面积可以用表达式表示为y=﹣(x﹣2)2+3,则要使重叠部分面积最大,x的值为( )
A.x=2 B.x=﹣2 C.x=3 D.x=﹣3
2.如图,已知在平面直角坐标系xOy中,抛物线C1:y=a1x2(a1≠0)与抛物线C2:y=a2x2+bx(a2≠0)的交点P在第三象限,过点P作x轴的平行线,与物线C1,C2分别交于点M,N.若=,则的值是( )
A. B.n﹣1 C.n D.
3.已知抛物线y=ax2+bx+c(a≠0)与y=x2-4x+3关于x轴对称,则a,b,c的值分别是( )
A.-1,4,-3 B.-1,-4,-3 C.-1,4,3 D.-1,-4,3
4.如图是二次函数的图象,其对称轴为直线,且过点.有以下四个结论:①,②,③,④若顶点坐标为,当时,y有最大值为2、最小值为,此时m的取值范围是.其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
5.将抛物线y=(x+2)2﹣3先向右平移1个单位长度,再向下平移2个单位长度后所得抛物线的解析式为( )
A.y=(x+3)2﹣5 B.y=(x+3)2﹣1 C.y=(x+1)2﹣1 D.y=(x+1)2﹣5
6.若y与x2成正比例,且当x=2时,y=4,则当x=﹣3时,y的值为( )
A.4 B.9 C.12 D.﹣5
7.将抛物线向左平移1个单位,得到的抛物线与y轴的交点坐标是( )
A.(0,2) B.(0,3) C.(0,4) D.(0,5)
8.在同一平面直角坐标系内,将函数的图象向右平移2个单位长度,再向下平移1个单位长度得到的图象的顶点坐标是( )
A.(2,-4) B.(4,-2) C.(2,-1) D.(-2,-1)
9.已知二次函数y=﹣2bx+6b的顶点为(m,n).当1≤m≤a时,5≤n≤9,则a的取值范围为( )
A.1<a≤3 B.3≤a≤5 C.3≤a≤5 D.5≤a≤7
10.在平面直角坐标系中,对于二次函数,下列说法中错误的是( )
A.y的最小值为1
B.图象顶点坐标为(2,1),对称轴为直线x=2
C.当时,y的值随x值的增大而增大,当时,y的值随x值的增大而减小
D.它的图象可由的图象向右平移2个单位长度,再向上平移1个单位长度得到
11.如图,已知抛物线与直线交于A,B两点.点M是直线AB上的一个动点,将点M向左平移4个单位长度得到点N,若线段MN与抛物线只有一个公共点,则点M的横坐标的取值范围是( )
A. B.或
C. D.或
12.已知函数,若使y=k成立的x值恰好有三个,则k的值为( )
A.0 B.1 C.2 D.3
13.如果在二次函数的表达式y=2x2+bx+c中,b>0,c<0,那么这个二次函数的图象可能是( )
A. B.
C. D.
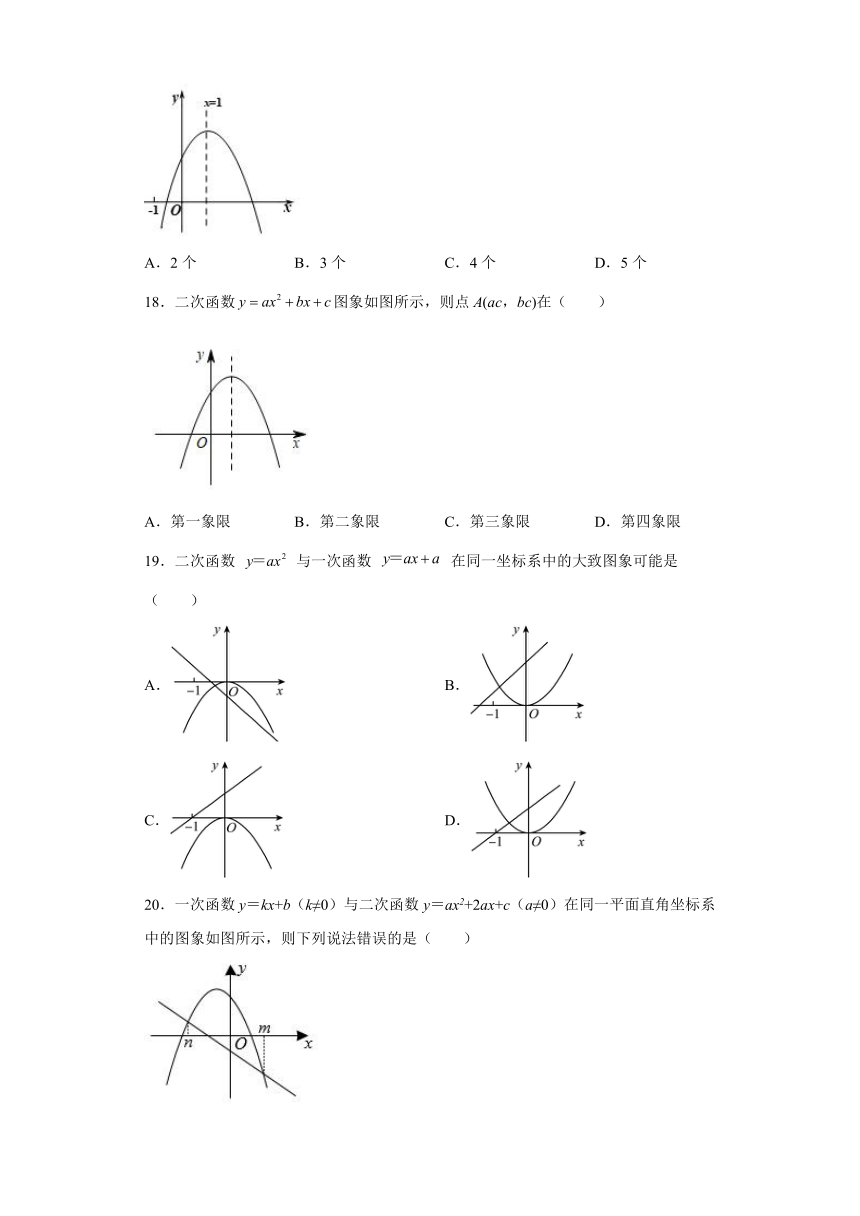
14.若一个二次函数y=ax2+bx+c(a>0)的图象经过五个点A(﹣1,n)、B(3,n)、C(m+1,y1)、D(1﹣m,y2)和E(1,y3),则下列关系正确的是( )
A.y1>y2>y3 B.y1=y2>y3 C.y1<y2<y3 D.y3>y1>y2
15.已知点是二次函数(a≠0)的图象上一个定点,而(m,n)是二次函数图象上动点,若对任意的实数m,都有,则( )
A. B. C. D.
16.如图所示,已知二次函数的图象与轴交于、两点,与轴交于点,.对称轴为直线,则下列结论:①;②;③;④是关于的一元二次方程的一个根,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
17.已知二次函数的图像如图所示,有下列5个结论:①;②;③;④;⑤,(的实数)其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
18.二次函数图象如图所示,则点A(ac,bc)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
19.二次函数 与一次函数 在同一坐标系中的大致图象可能是( )
A. B.
C. D.
20.一次函数y=kx+b(k≠0)与二次函数y=ax2+2ax+c(a≠0)在同一平面直角坐标系中的图象如图所示,则下列说法错误的是( )
A.ax2+2ax﹣b>kx﹣c时,n<x<m
B.当x≥0时,ax2+2ax+c≤c
C.若(﹣,y1)在二次函数y=ax2+2ax+c图象上,则y1<c
D.﹣ac+bk>0
21.如果两个不同的二次函数的图象相交,那么它们的交点最多有( )
A.1 个 B.2 个 C.3 个 D.4 个
22.函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )
① ;②; ③;④将图象向上平移1个单位后与直线有3个交点.
A.①② B.①③ C.②③④ D.①③④
23.一元二次方程的两个根分别为和,则二次函数 的对称轴是( )
A. B. C. D.
24.已知关于x的二次函数,当时,y在时取得最大值,则实数a的取值范围是( )
A. B. C. D.
25.已知抛物线具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等,点M的坐标为(3,6),P是抛物线上一动点,则△PMF周长的最小值是( )
A.5 B.9 C.11 D.13
二、填空题
26.已知二次函数,如果当x=-1时y=2,那么当x=1时,y=_____.
27.把二次函数用配方法化成的形式是________.
28.函数,当-3≤x≤3时,y的取值范围是____.
29.二次函数的对称轴是直线________;函数的图象的对称轴是直线________.
三、解答题
30.在平面直角坐标系xOy中,已知抛物线y=x-2x,M(x1,m)、N(x2,m)(x1<x2)是此抛物线上的两点.
(1)求抛物线顶点坐标
(2)若3x2-x1=10,求m的值.
(3)若线段MN的长度不小于10,求m的最小值.
31.在平面直角坐标系中,设二次函数y1=ax2+bx+c,y2=cx2+bx+a(a,b,c是实数,ac<0).
(1)若函数y1的对称轴为直线x=1,且函数y1的图象经过点(a,c),求a,b的值.
(2)设函数y1的最大值为m,函数y2的最小值为n,若m+n=0,求证:a+c=0.
(3)若函数y1的图象与函数y2的图象的两个交点分别在一、三象限,求证:b>0.
参考答案
1.A
2.B
3.A
4.A
5.D
6.B
7.B
8.C
9.B
10.C
11.B
12.D
13.B
14.B
15.D
16.A
17.B
18.B
19.D
20.C
21.B
22.D
23.A
24.B
25.C
26.2
27.
28.-34≤y≤-9
29.2 -1
30.(1)
(2)3
(3)24
31.(1)解:∵函数y1的对称轴为直线x=1,
∴﹣=1,①
∵函数y1的图象经过点(a,c),
∴a×a2+ab+c=c,②
联立①②,解得,
即a的值为2,b的值为-4;
(2)证明:∵函数y1的最大值为m,
∴a<0,m=,
∵函数y2的最小值为n,
∴c>0,n=,
∵m+n=0,
∴=0,
整理,得
,
∵ac<0,
∴4ac-b2<0,
∴a+c=0;
(3)证明:∵函数y1的图象与函数y2的图象的两个交点分别在一、三象限,且ac<0,
①若a<0,c>0,
则,
即>0,
∵a<0,c>0,
∴ac<0,a﹣c<0,
∴b>0,
②若a>0,c<0,
则<﹣,
即<0,
∵a<0,c>0,
∴ac<0,a﹣c>0,
∴b>0,
综合①②,得b>0.
班级: 姓名: 成绩:
一、选择题
1.若两个图形重叠后.重叠部分的面积可以用表达式表示为y=﹣(x﹣2)2+3,则要使重叠部分面积最大,x的值为( )
A.x=2 B.x=﹣2 C.x=3 D.x=﹣3
2.如图,已知在平面直角坐标系xOy中,抛物线C1:y=a1x2(a1≠0)与抛物线C2:y=a2x2+bx(a2≠0)的交点P在第三象限,过点P作x轴的平行线,与物线C1,C2分别交于点M,N.若=,则的值是( )
A. B.n﹣1 C.n D.
3.已知抛物线y=ax2+bx+c(a≠0)与y=x2-4x+3关于x轴对称,则a,b,c的值分别是( )
A.-1,4,-3 B.-1,-4,-3 C.-1,4,3 D.-1,-4,3
4.如图是二次函数的图象,其对称轴为直线,且过点.有以下四个结论:①,②,③,④若顶点坐标为,当时,y有最大值为2、最小值为,此时m的取值范围是.其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
5.将抛物线y=(x+2)2﹣3先向右平移1个单位长度,再向下平移2个单位长度后所得抛物线的解析式为( )
A.y=(x+3)2﹣5 B.y=(x+3)2﹣1 C.y=(x+1)2﹣1 D.y=(x+1)2﹣5
6.若y与x2成正比例,且当x=2时,y=4,则当x=﹣3时,y的值为( )
A.4 B.9 C.12 D.﹣5
7.将抛物线向左平移1个单位,得到的抛物线与y轴的交点坐标是( )
A.(0,2) B.(0,3) C.(0,4) D.(0,5)
8.在同一平面直角坐标系内,将函数的图象向右平移2个单位长度,再向下平移1个单位长度得到的图象的顶点坐标是( )
A.(2,-4) B.(4,-2) C.(2,-1) D.(-2,-1)
9.已知二次函数y=﹣2bx+6b的顶点为(m,n).当1≤m≤a时,5≤n≤9,则a的取值范围为( )
A.1<a≤3 B.3≤a≤5 C.3≤a≤5 D.5≤a≤7
10.在平面直角坐标系中,对于二次函数,下列说法中错误的是( )
A.y的最小值为1
B.图象顶点坐标为(2,1),对称轴为直线x=2
C.当时,y的值随x值的增大而增大,当时,y的值随x值的增大而减小
D.它的图象可由的图象向右平移2个单位长度,再向上平移1个单位长度得到
11.如图,已知抛物线与直线交于A,B两点.点M是直线AB上的一个动点,将点M向左平移4个单位长度得到点N,若线段MN与抛物线只有一个公共点,则点M的横坐标的取值范围是( )
A. B.或
C. D.或
12.已知函数,若使y=k成立的x值恰好有三个,则k的值为( )
A.0 B.1 C.2 D.3
13.如果在二次函数的表达式y=2x2+bx+c中,b>0,c<0,那么这个二次函数的图象可能是( )
A. B.
C. D.
14.若一个二次函数y=ax2+bx+c(a>0)的图象经过五个点A(﹣1,n)、B(3,n)、C(m+1,y1)、D(1﹣m,y2)和E(1,y3),则下列关系正确的是( )
A.y1>y2>y3 B.y1=y2>y3 C.y1<y2<y3 D.y3>y1>y2
15.已知点是二次函数(a≠0)的图象上一个定点,而(m,n)是二次函数图象上动点,若对任意的实数m,都有,则( )
A. B. C. D.
16.如图所示,已知二次函数的图象与轴交于、两点,与轴交于点,.对称轴为直线,则下列结论:①;②;③;④是关于的一元二次方程的一个根,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
17.已知二次函数的图像如图所示,有下列5个结论:①;②;③;④;⑤,(的实数)其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
18.二次函数图象如图所示,则点A(ac,bc)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
19.二次函数 与一次函数 在同一坐标系中的大致图象可能是( )
A. B.
C. D.
20.一次函数y=kx+b(k≠0)与二次函数y=ax2+2ax+c(a≠0)在同一平面直角坐标系中的图象如图所示,则下列说法错误的是( )
A.ax2+2ax﹣b>kx﹣c时,n<x<m
B.当x≥0时,ax2+2ax+c≤c
C.若(﹣,y1)在二次函数y=ax2+2ax+c图象上,则y1<c
D.﹣ac+bk>0
21.如果两个不同的二次函数的图象相交,那么它们的交点最多有( )
A.1 个 B.2 个 C.3 个 D.4 个
22.函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )
① ;②; ③;④将图象向上平移1个单位后与直线有3个交点.
A.①② B.①③ C.②③④ D.①③④
23.一元二次方程的两个根分别为和,则二次函数 的对称轴是( )
A. B. C. D.
24.已知关于x的二次函数,当时,y在时取得最大值,则实数a的取值范围是( )
A. B. C. D.
25.已知抛物线具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等,点M的坐标为(3,6),P是抛物线上一动点,则△PMF周长的最小值是( )
A.5 B.9 C.11 D.13
二、填空题
26.已知二次函数,如果当x=-1时y=2,那么当x=1时,y=_____.
27.把二次函数用配方法化成的形式是________.
28.函数,当-3≤x≤3时,y的取值范围是____.
29.二次函数的对称轴是直线________;函数的图象的对称轴是直线________.
三、解答题
30.在平面直角坐标系xOy中,已知抛物线y=x-2x,M(x1,m)、N(x2,m)(x1<x2)是此抛物线上的两点.
(1)求抛物线顶点坐标
(2)若3x2-x1=10,求m的值.
(3)若线段MN的长度不小于10,求m的最小值.
31.在平面直角坐标系中,设二次函数y1=ax2+bx+c,y2=cx2+bx+a(a,b,c是实数,ac<0).
(1)若函数y1的对称轴为直线x=1,且函数y1的图象经过点(a,c),求a,b的值.
(2)设函数y1的最大值为m,函数y2的最小值为n,若m+n=0,求证:a+c=0.
(3)若函数y1的图象与函数y2的图象的两个交点分别在一、三象限,求证:b>0.
参考答案
1.A
2.B
3.A
4.A
5.D
6.B
7.B
8.C
9.B
10.C
11.B
12.D
13.B
14.B
15.D
16.A
17.B
18.B
19.D
20.C
21.B
22.D
23.A
24.B
25.C
26.2
27.
28.-34≤y≤-9
29.2 -1
30.(1)
(2)3
(3)24
31.(1)解:∵函数y1的对称轴为直线x=1,
∴﹣=1,①
∵函数y1的图象经过点(a,c),
∴a×a2+ab+c=c,②
联立①②,解得,
即a的值为2,b的值为-4;
(2)证明:∵函数y1的最大值为m,
∴a<0,m=,
∵函数y2的最小值为n,
∴c>0,n=,
∵m+n=0,
∴=0,
整理,得
,
∵ac<0,
∴4ac-b2<0,
∴a+c=0;
(3)证明:∵函数y1的图象与函数y2的图象的两个交点分别在一、三象限,且ac<0,
①若a<0,c>0,
则,
即>0,
∵a<0,c>0,
∴ac<0,a﹣c<0,
∴b>0,
②若a>0,c<0,
则<﹣,
即<0,
∵a<0,c>0,
∴ac<0,a﹣c>0,
∴b>0,
综合①②,得b>0.
同课章节目录
