苏科版九年级数学上册2.2圆的对称性 同步练习题 (含答案)
文档属性
| 名称 | 苏科版九年级数学上册2.2圆的对称性 同步练习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 409.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 16:37:39 | ||
图片预览



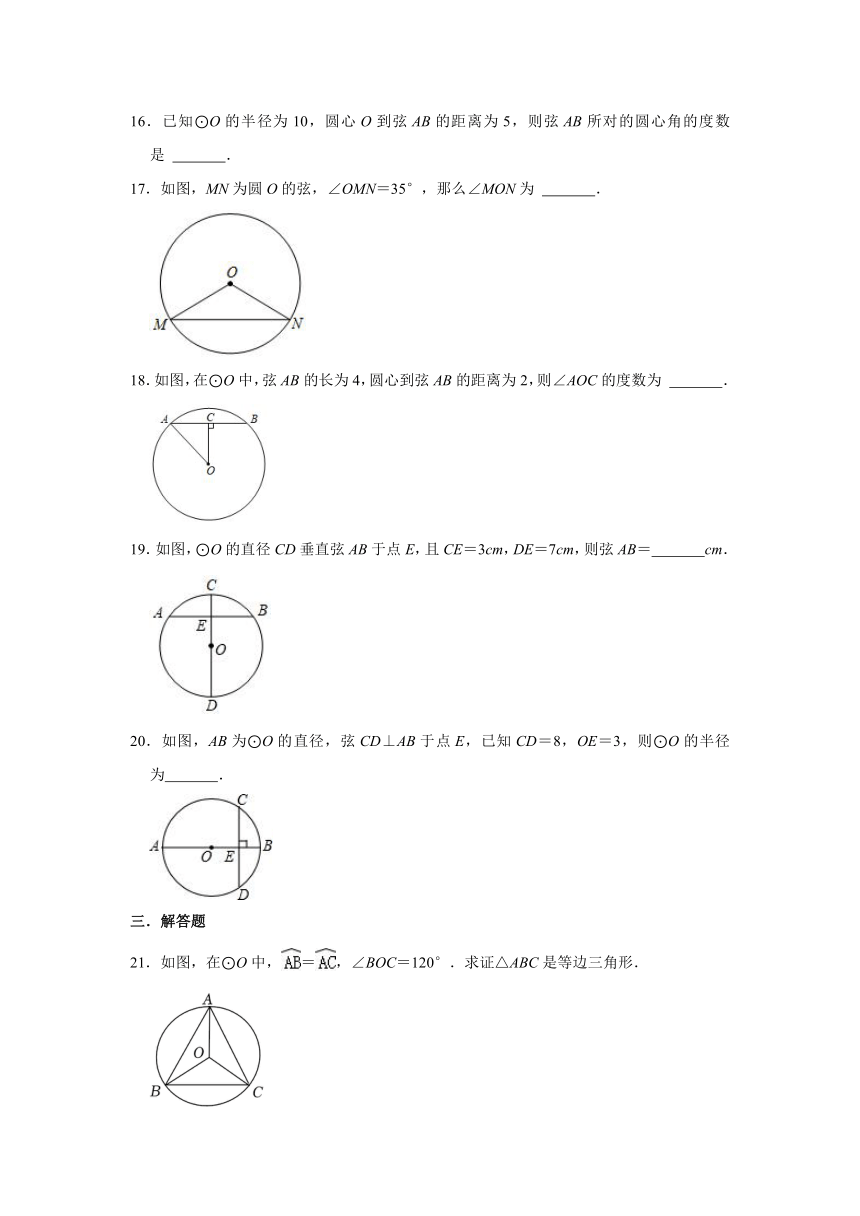

文档简介
2022-2023学年苏科版九年级数学上册《2.2圆的对称性》同步练习题(附答案)
一.选择题
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果AB=20,CD=16,那么线段OE的长为( )
A.4 B.6 C.8 D.9
2.下列图形中的角,是圆心角的为( )
A. B.
C. D.
3.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
4.如图所示,⊙O的直径为20,弦AB的长度是16,ON⊥AB,垂足为N,则ON的长度为( )
A.4 B.6 C.8 D.10
5.下列语句,错误的是( )
A.直径是弦
B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心
D.平分弧的半径垂直于弧所对的弦
6.一条排水管的截面如图所示,已知排水管的半径OB=5,水面宽AB=8,则截面圆心O到水面的距离OC是( )
A.4 B.3 C.2 D.1
7.下列结论中,正确的是( )
A.长度相等的两条弧是等弧
B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦
D.圆是中心对称图形
8.如图,在⊙O中,=,∠1=45°,则∠2=( )
A.60° B.30° C.45° D.40°
9.如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )
A.AE=BE B.CE=DE C.弧AC=弧BC D.弧AD=弧BD
二.填空题
10.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的垂线段OE长为3cm,则半径OA的长为 cm.
11.如图,在⊙O中,,A、C之间的距离为4,则线段BD= .
12.如图,在半径为10cm的⊙O中,AB=16cm,OC⊥AB于点C,则OC等于 cm.
13.如图,⊙O的弦AB垂直平分半径OC,若AB=,则⊙O的半径为 .
14.如图,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是 .
15.在半径为9cm的圆中,60°的圆心角所对的弦长为 cm.
16.已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆心角的度数是 .
17.如图,MN为圆O的弦,∠OMN=35°,那么∠MON为 .
18.如图,在⊙O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为 .
19.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
20.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,OE=3,则⊙O的半径为 .
三.解答题
21.如图,在⊙O中,=,∠BOC=120°.求证△ABC是等边三角形.
22.如图所示,AB、CD是⊙O的两条直径,CE∥AB,求证:=.
23.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=2,AE=5,则⊙O的直径是多少?
24.已知线段AD、BC为⊙O的弦,且BC=AD,求证:AB=CD.
25.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
26.如图,AB是⊙O的直径,CD是⊙O的弦,BA、DC的延长线交于点E,AB=2CE,∠E=20°,求∠BOD的度数.
参考答案
一.选择题
1.解:∵AB=20,
∴OD=10,
∵CD⊥AB,
∴DE==,
在Rt△DOE中,
OE===6.
故选:B.
2.解:A.顶点不在圆上,不是圆心角,故本选项不符合题意;
B.顶点不在圆上,不是圆心角,故本选项不符合题意;
C.是圆心角,故本选项符合题意;
D.顶点不在圆上,不是圆心角,故本选项不符合题意;
故选:C.
3.解:过O点作OH⊥AB于H,连接OA,如图,则AH=BH=AB=3,
在Rt△OAH中,OH===4,
所以OP的范围为4≤OP<5.
故选:B.
4.解:由题意可得,
OA=10,∠ONA=90°,AB=16,
∴AN=8,
∴ON=,
故选:B.
5.解:直径是弦,A正确,不符合题意;
在同圆或等圆中,相等的圆心角所对的弧相等,B错误,符合题意;
弦的垂直平分线一定经过圆心,C正确,不符合题意;
平分弧的半径垂直于弧所对的弦,D正确,不符合题意;
故选:B.
6.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×8=4,
在Rt△OCB中,由勾股定理得:OC===3,
故选:B.
7.解:A、长度相等的弧不一定是等弧,故错误;
B、同圆或等圆中,相等的圆心角所对的弧相等,故错误;
C、此弦不能是直径,命题错误;
D、圆是中心对称图形,正确,
故选:D.
8.解:∵=,
∴∠2=∠1=45°,
故选:C.
9.解:∵CD⊥AB,CD为直径,
∴AE=BE,弧AD=弧BD,弧AC=弧BC,
CE>DE,
故选:B.
二.填空题
10.解:∵OE⊥AB,AB=8,
∴AE=BE=4,
在Rt△AOE中,OE=3,
根据勾股定理得:OA=.
11.解:如图,连接BD,AC.
∵,
∴,
∴,
∴BD=AC=4,
故答案为4.
12.解:连接OA,如图,
∵OC⊥AB,
∴AC=BC=AB=8,
在Rt△OAC中,OC===6(cm).
故答案为6.
13.解:连OA,AB交OC于D点,如图,
设半径为R,
∵AB垂直平分半径OC,
∴DA=DB,OD=OC,
而AB=,
∴AD=,
在Rt△AOD中,OD=R,
∵OA2=AD2+OD2,即R2=()2+(R)2,
∴R=.
故答案为.
14.解:如图:连接OA,作OM⊥AB与M,
∵⊙O的直径为10,
∴半径为5,
∴OP的最大值为5,
∵OM⊥AB与M,
∴AM=BM,
∵AB=8,
∴AM=4,
在Rt△AOM中,OM=,
OM的长即为OP的最小值,
∴3≤OP≤5.
15.解:由题意知,设圆心为O,60°的圆心角的两边与圆的交点分别为A,B,则△AOB是等边三角形,∴AO=AB=OB=9cm.
16.解:由图可知,OA=10,OD=5,
在Rt△OAD中,
∴sinA==,
∴∠A=30°,
∴∠1=60°,
同理可得∠2=60°,
∴∠AOB=∠1+∠2=60°+60°=120°,
∴弦AB所对的圆心角的度数是120°.
故答案为:120°.
17.解:∵MN为圆O的弦,
∴OM=ON,
∴∠OMN=∠ONM=35°,
∴∠MON=180°﹣2∠OMN=180°﹣2×35°=110°.
故答案为:110°.
18.解:∵OC⊥AB,
∴AC=BC==2,
∵OC=2,
∴△AOC为等腰直角三角形,
∴∠AOC=45°,
故答案为:45°.
19.解:连接OA,如图,
∵CE=3cm,DE=7cm,
∴CD=10cm,
∴OC=OA=5cm,OE=2cm,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==(cm),
∴AB=2AE=2(cm).
故答案为2.
20.解:连接OD,
∵CD⊥AB于点E,直径AB过O,
∴DE=CE=CD=×8=4,∠OED=90°,
由勾股定理得:OD===5,
即⊙O的半径为5.
故答案为:5.
三.解答题
21.证明:∵,
∴AB=AC,
∵∠BOC=120°,
∴∠BAC=60°,
∴△ABC是等边三角形.
22.证明:连接OE,
∵CE∥AB,
∴∠BOC=∠C,∠AOE=∠E,
∵OC=OE,
∴∠C=∠E,
∴∠BOC=∠AOE,
∴=.
23.解:设⊙O的半径为r,
∵AB为⊙O的直径,弦CD⊥AB,CD=2,AE=5,
∴CE=1,OE=5﹣r,
在Rt△OCE中,
OC2=OE2+CE2,即r2=(5﹣r)2+1,
解得,r=2.6,
∴AB=2r=5.2,
答:⊙O的直径是5.2.
24.证明:∵BC=AD,
∴=,
即+=+,
∴=,
∴AB=CD.
25.证明:∵AB=CD,
∴=,
∴﹣=﹣,即=,
∴∠C=∠B,
∴CE=BE.
26.解:如图,连接CO,
∵AB是⊙O的直径,AB=2CE,
∴CE=OC,
∵∠E=20°,
∴∠COE=∠E=20°,
∴∠DCO=∠COE+∠E=40°,
∵OC=OD,
∴∠DCO=∠D=40°,
∴∠BOD=∠E+∠D=60°.
一.选择题
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果AB=20,CD=16,那么线段OE的长为( )
A.4 B.6 C.8 D.9
2.下列图形中的角,是圆心角的为( )
A. B.
C. D.
3.如图,⊙O的半径为5,弦AB=6,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
4.如图所示,⊙O的直径为20,弦AB的长度是16,ON⊥AB,垂足为N,则ON的长度为( )
A.4 B.6 C.8 D.10
5.下列语句,错误的是( )
A.直径是弦
B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心
D.平分弧的半径垂直于弧所对的弦
6.一条排水管的截面如图所示,已知排水管的半径OB=5,水面宽AB=8,则截面圆心O到水面的距离OC是( )
A.4 B.3 C.2 D.1
7.下列结论中,正确的是( )
A.长度相等的两条弧是等弧
B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦
D.圆是中心对称图形
8.如图,在⊙O中,=,∠1=45°,则∠2=( )
A.60° B.30° C.45° D.40°
9.如图,在⊙O中,弦AB与直径CD垂直,垂足为E,则下列结论中错误的是( )
A.AE=BE B.CE=DE C.弧AC=弧BC D.弧AD=弧BD
二.填空题
10.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的垂线段OE长为3cm,则半径OA的长为 cm.
11.如图,在⊙O中,,A、C之间的距离为4,则线段BD= .
12.如图,在半径为10cm的⊙O中,AB=16cm,OC⊥AB于点C,则OC等于 cm.
13.如图,⊙O的弦AB垂直平分半径OC,若AB=,则⊙O的半径为 .
14.如图,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是 .
15.在半径为9cm的圆中,60°的圆心角所对的弦长为 cm.
16.已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆心角的度数是 .
17.如图,MN为圆O的弦,∠OMN=35°,那么∠MON为 .
18.如图,在⊙O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为 .
19.如图,⊙O的直径CD垂直弦AB于点E,且CE=3cm,DE=7cm,则弦AB= cm.
20.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=8,OE=3,则⊙O的半径为 .
三.解答题
21.如图,在⊙O中,=,∠BOC=120°.求证△ABC是等边三角形.
22.如图所示,AB、CD是⊙O的两条直径,CE∥AB,求证:=.
23.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=2,AE=5,则⊙O的直径是多少?
24.已知线段AD、BC为⊙O的弦,且BC=AD,求证:AB=CD.
25.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
26.如图,AB是⊙O的直径,CD是⊙O的弦,BA、DC的延长线交于点E,AB=2CE,∠E=20°,求∠BOD的度数.
参考答案
一.选择题
1.解:∵AB=20,
∴OD=10,
∵CD⊥AB,
∴DE==,
在Rt△DOE中,
OE===6.
故选:B.
2.解:A.顶点不在圆上,不是圆心角,故本选项不符合题意;
B.顶点不在圆上,不是圆心角,故本选项不符合题意;
C.是圆心角,故本选项符合题意;
D.顶点不在圆上,不是圆心角,故本选项不符合题意;
故选:C.
3.解:过O点作OH⊥AB于H,连接OA,如图,则AH=BH=AB=3,
在Rt△OAH中,OH===4,
所以OP的范围为4≤OP<5.
故选:B.
4.解:由题意可得,
OA=10,∠ONA=90°,AB=16,
∴AN=8,
∴ON=,
故选:B.
5.解:直径是弦,A正确,不符合题意;
在同圆或等圆中,相等的圆心角所对的弧相等,B错误,符合题意;
弦的垂直平分线一定经过圆心,C正确,不符合题意;
平分弧的半径垂直于弧所对的弦,D正确,不符合题意;
故选:B.
6.解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×8=4,
在Rt△OCB中,由勾股定理得:OC===3,
故选:B.
7.解:A、长度相等的弧不一定是等弧,故错误;
B、同圆或等圆中,相等的圆心角所对的弧相等,故错误;
C、此弦不能是直径,命题错误;
D、圆是中心对称图形,正确,
故选:D.
8.解:∵=,
∴∠2=∠1=45°,
故选:C.
9.解:∵CD⊥AB,CD为直径,
∴AE=BE,弧AD=弧BD,弧AC=弧BC,
CE>DE,
故选:B.
二.填空题
10.解:∵OE⊥AB,AB=8,
∴AE=BE=4,
在Rt△AOE中,OE=3,
根据勾股定理得:OA=.
11.解:如图,连接BD,AC.
∵,
∴,
∴,
∴BD=AC=4,
故答案为4.
12.解:连接OA,如图,
∵OC⊥AB,
∴AC=BC=AB=8,
在Rt△OAC中,OC===6(cm).
故答案为6.
13.解:连OA,AB交OC于D点,如图,
设半径为R,
∵AB垂直平分半径OC,
∴DA=DB,OD=OC,
而AB=,
∴AD=,
在Rt△AOD中,OD=R,
∵OA2=AD2+OD2,即R2=()2+(R)2,
∴R=.
故答案为.
14.解:如图:连接OA,作OM⊥AB与M,
∵⊙O的直径为10,
∴半径为5,
∴OP的最大值为5,
∵OM⊥AB与M,
∴AM=BM,
∵AB=8,
∴AM=4,
在Rt△AOM中,OM=,
OM的长即为OP的最小值,
∴3≤OP≤5.
15.解:由题意知,设圆心为O,60°的圆心角的两边与圆的交点分别为A,B,则△AOB是等边三角形,∴AO=AB=OB=9cm.
16.解:由图可知,OA=10,OD=5,
在Rt△OAD中,
∴sinA==,
∴∠A=30°,
∴∠1=60°,
同理可得∠2=60°,
∴∠AOB=∠1+∠2=60°+60°=120°,
∴弦AB所对的圆心角的度数是120°.
故答案为:120°.
17.解:∵MN为圆O的弦,
∴OM=ON,
∴∠OMN=∠ONM=35°,
∴∠MON=180°﹣2∠OMN=180°﹣2×35°=110°.
故答案为:110°.
18.解:∵OC⊥AB,
∴AC=BC==2,
∵OC=2,
∴△AOC为等腰直角三角形,
∴∠AOC=45°,
故答案为:45°.
19.解:连接OA,如图,
∵CE=3cm,DE=7cm,
∴CD=10cm,
∴OC=OA=5cm,OE=2cm,
∵AB⊥CD,
∴AE=BE,
在Rt△AOE中,AE==(cm),
∴AB=2AE=2(cm).
故答案为2.
20.解:连接OD,
∵CD⊥AB于点E,直径AB过O,
∴DE=CE=CD=×8=4,∠OED=90°,
由勾股定理得:OD===5,
即⊙O的半径为5.
故答案为:5.
三.解答题
21.证明:∵,
∴AB=AC,
∵∠BOC=120°,
∴∠BAC=60°,
∴△ABC是等边三角形.
22.证明:连接OE,
∵CE∥AB,
∴∠BOC=∠C,∠AOE=∠E,
∵OC=OE,
∴∠C=∠E,
∴∠BOC=∠AOE,
∴=.
23.解:设⊙O的半径为r,
∵AB为⊙O的直径,弦CD⊥AB,CD=2,AE=5,
∴CE=1,OE=5﹣r,
在Rt△OCE中,
OC2=OE2+CE2,即r2=(5﹣r)2+1,
解得,r=2.6,
∴AB=2r=5.2,
答:⊙O的直径是5.2.
24.证明:∵BC=AD,
∴=,
即+=+,
∴=,
∴AB=CD.
25.证明:∵AB=CD,
∴=,
∴﹣=﹣,即=,
∴∠C=∠B,
∴CE=BE.
26.解:如图,连接CO,
∵AB是⊙O的直径,AB=2CE,
∴CE=OC,
∵∠E=20°,
∴∠COE=∠E=20°,
∴∠DCO=∠COE+∠E=40°,
∵OC=OD,
∴∠DCO=∠D=40°,
∴∠BOD=∠E+∠D=60°.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
