6.5一次函数图象的应用[上学期]

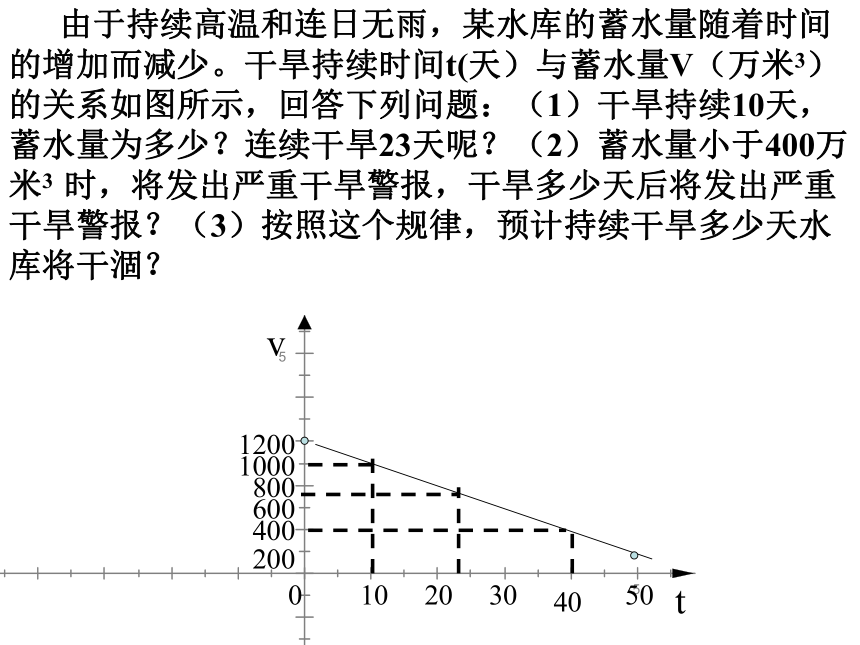
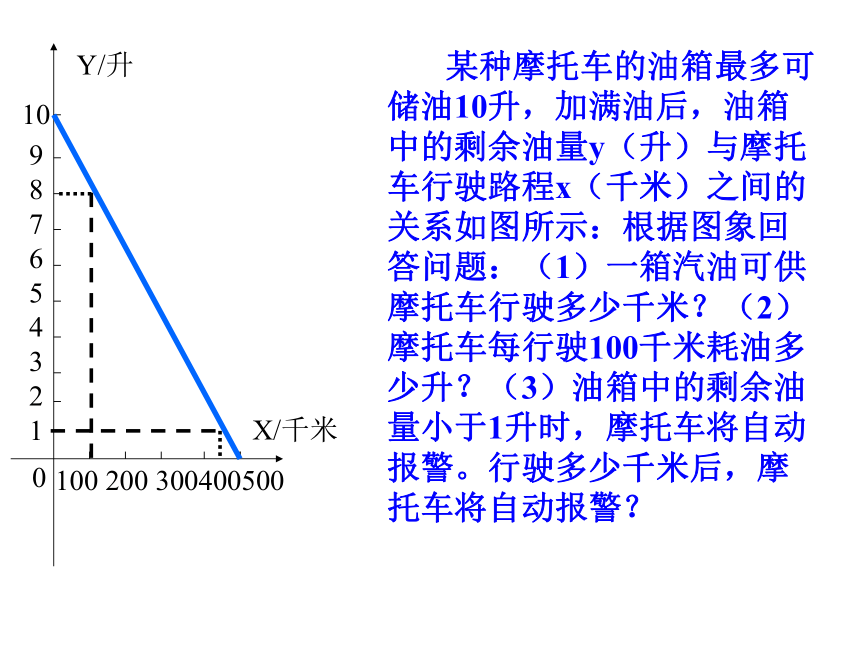
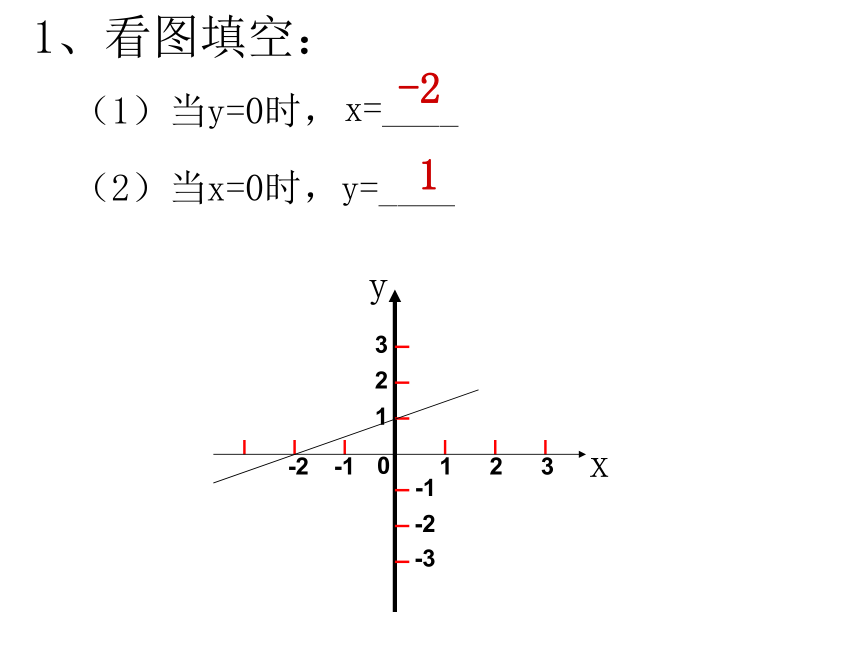
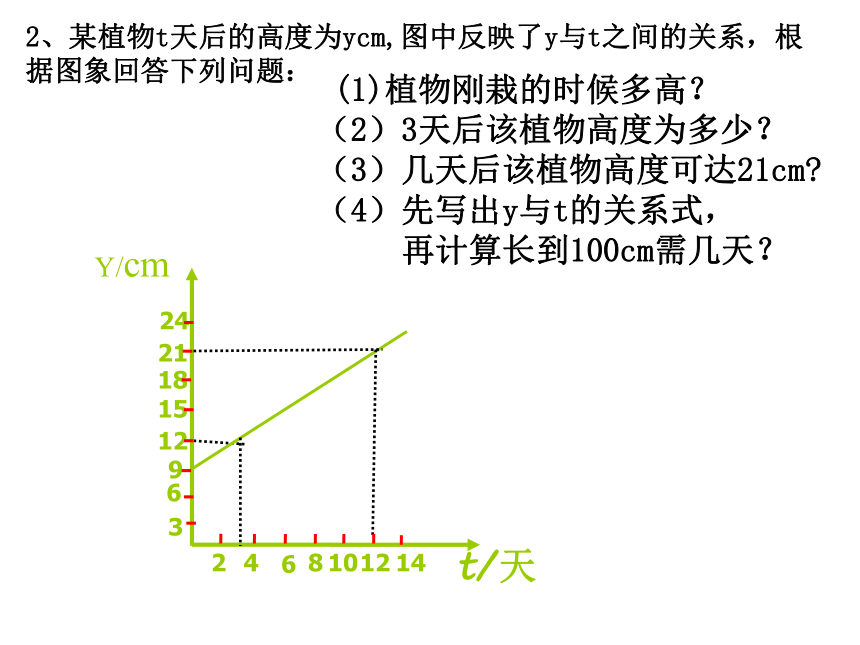
课件16张PPT。6.5一次函数图象的应用XYO 由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少。干旱持续时间t(天）与蓄水量V（万米3）的关系如图所示，回答下列问题：（1）干旱持续10天，蓄水量为多少？连续干旱23天呢？（2）蓄水量小于400万米3 时，将发出严重干旱警报，干旱多少天后将发出严重干旱警报？（3）按照这个规律，预计持续干旱多少天水库将干涸？tv1020304020040060080010001200500 100 200 30040050098765432110X/千米Y/升 某种摩托车的油箱最多可储油10升，加满油后，油箱中的剩余油量y（升）与摩托车行驶路程x（千米）之间的关系如图所示：根据图象回答问题：（1）一箱汽油可供摩托车行驶多少千米？（2）摩托车每行驶100千米耗油多少升？（3）油箱中的剩余油量小于1升时，摩托车将自动报警。行驶多少千米后，摩托车将自动报警？0x=____-2 2013123-1-2-1-2-3（1）当y=0时，（2）当x=0时，y=____xy1 1、看图填空：2、某植物t天后的高度为ycm,图中反映了y与t之间的关系，根据图象回答下列问题： (1)植物刚栽的时候多高？
（2）3天后该植物高度为多少？
（3）几天后该植物高度可达21cm?
（4）先写出y与t的关系式，
再计算长到100cm需几天？96312151821242468101214t/天Y/cm议一议：
一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系？ 从”数”的方面看,当一次函数 y=0.5x+1 的函
数值为0时,相应的自变量的值即为方程 0.5x+1=0 的
解: 从”行”的方面看,函数 y=0.5x+1 与 x 轴交点的
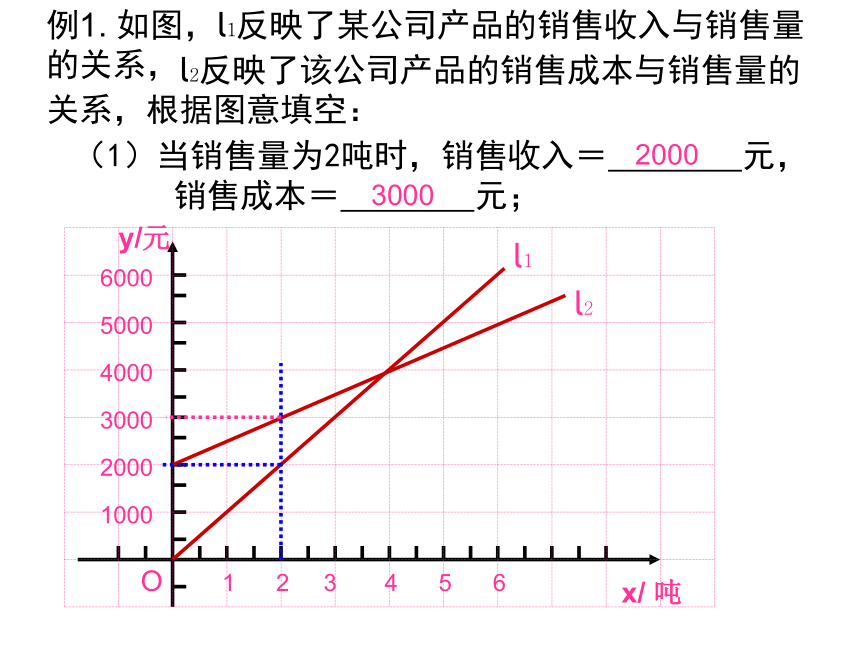
横坐标即为方程 0.5x+1=0 的解. 例1. 如图，l1反映了某公司产品的销售收入与销售量的关系，（1）当销售量为2吨时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；20003000　　　　l2反映了该公司产品的销售成本与销售量的关系，根据图意填空：（2）当销售量为6吨时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；60005000（3）当销售量为　　时，销售收入等于销售成本；4吨（4）当销售量　　　　时，该公司赢利（收入大于成本）；
　　当销售量　　　　时，该公司亏损（收入小于成本）；大于4吨小于4吨（5） l1对应的函数表达式是　　　　　　　　，
　　 l2对应的函数表达式是　　　　　　　　。y=1000xy=500x+2000 例2　　我边防局接到情报，近海处有一可疑船只A正向公海方向行驶。边防局迅速派出快艇B追赶（如下图），海
岸公
海AB下图中l1 ，l2分别表示两船相对于海岸的距离s（海里）
与追赶时间t（分）之间的关系。根据图象回答下列问题：（1）哪条线表示B到海岸的距离与追赶时间之间的关系？解：观察图象，得当t＝0时，B距海岸0海里，即
　　　　　　　　　　　　　　　　S＝0，故l1表
　　　　　　　　　　　　　　　　示B到海岸的距
　　　　　　　　　　　　　　　　离与追赶时间之
　　　　　　　　　　　　　　　　间的关系；（2）A、B哪个速度快？从0增加到10时， l2的纵坐标增加了2，而l1的纵坐标增加了5，即10分内，A行驶了2海里，B行驶了5海里，所以B的速度快。（3）15分内B能否追上A？l1l2延长l1，l2，　　　　　可以看出，当t＝15时，l1上对应点在l2
上对应点的下方，这表明，15分时B尚未追上A。　　如图l1 ，l2相交于点P。（4）如果一直追下去，那么B能否追上A？l1l2因此，如果一直追下去，那么B一定能追上A。P（5）当A逃到离海岸12海里的公海时，B将无法对其进行检查。照此速度，B能否在A逃入公海前将其拦截？l1l2P　　从图中可以看出，l1与l1交点P的纵坐标小于12，　想一想你能用其他方法解决
上述问题吗？这说明在A逃入公海前，我边防快艇B能够追上A。课堂练习:
P178~P183 课外作业:
1、<同步>P81~P84

2、<动态全解>